3. 图像处理

图像处理

成像原理与数字化

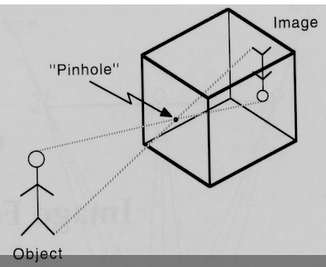
• 小孔成像（Pinhole）
  小孔成像的基本原理如下图所示：
  
  
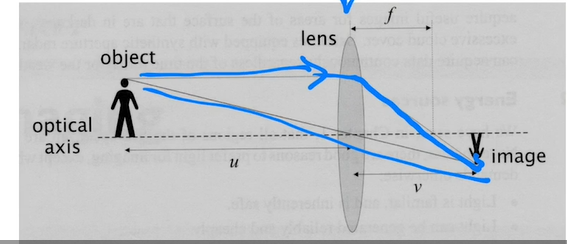
• 透镜成像
  
  
• CCD/CMOS（电荷耦合）成像
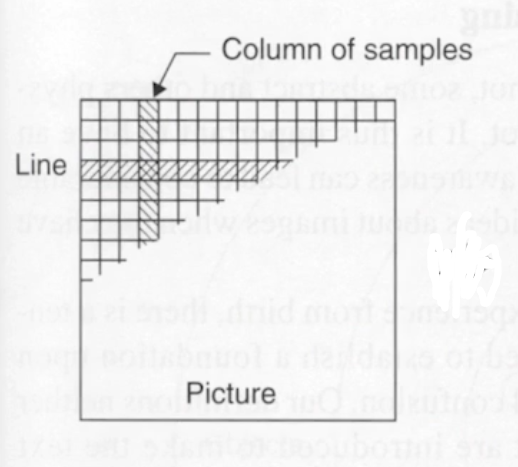
  在CCD成像当中，通过透镜后的像会呈现在CMOS上，COMS会将呈现数字化，这一过程中有两个重要的步骤：
  1. 抽样（Sampling）
     将图像转化为有限的单位像素，如图所示：
     
     
  2. 量化（Quantization）
     用整数表示单位像素的值，对于8bit而言，单位像素的明暗程度以0~255的灰度值来表示，0表示黑色，255表示白色。
  现在，一幅黑白的图像中的每一个单位像素点都用一个整数来表示其黑白的程度，那么整张图片就可以用一个只有整数的矩阵来表示（单通道）。
  对于彩色的图像，通常以RGB（红色、绿色、蓝色）的三种程度（三通道）来进行量化，因此彩色图片的一个单位像素点以一个三维的向量，通常是\([R,G,B]\)来表示。最终三个矩阵表示一幅彩色图像，这个过程叫做张量（Tensor）。
  ## 点处理(Point Processing) 图像的点处理是： 设定图像上一个像素值\(r(x,y)\),经过处理\(s(x,y)=T(r(x,y))\)后，得到同一位置的像素\(s(x,y)\)。
  注意：

1. \((x,y)\)表示坐标。
2. 不同的图像处理库其坐标系统的原点设置不同，y的取值设定也不同。
   
3. \(T\)只能是单调（通常是单调递增）的函数。 ### 常见的点处理变换

• 阈值变换(Thresholding)
  函数图像
  
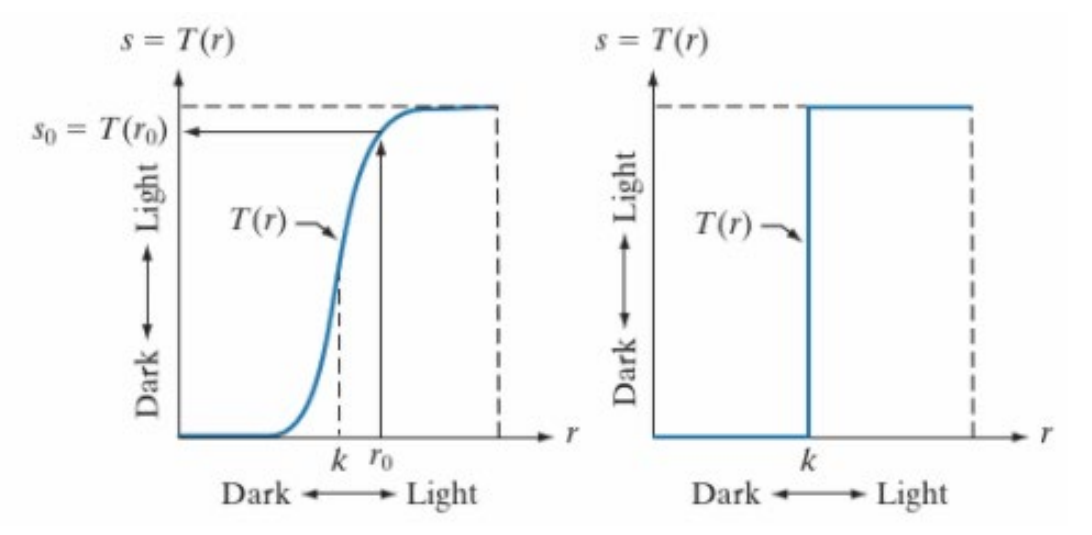
  阈值函数可分为两种：软阈值函数（左）和硬阈值函数/二值化函数(Hard thresholding/Binarization，右),它们的作用都是将像素转换成黑白像素。
  图像中的\(m\)点称为阈值，高于阈值的像素将会被强化为近黑色/黑色的像素值，低于阈值的像素值将被弱化为近白色/白色的像素值。

• 像素反转 \[s=L-1-r\] \(L\)表示最大的像素值。
  作用是将像素值进行翻转，白色变为黑色，黑色变为白色。
  

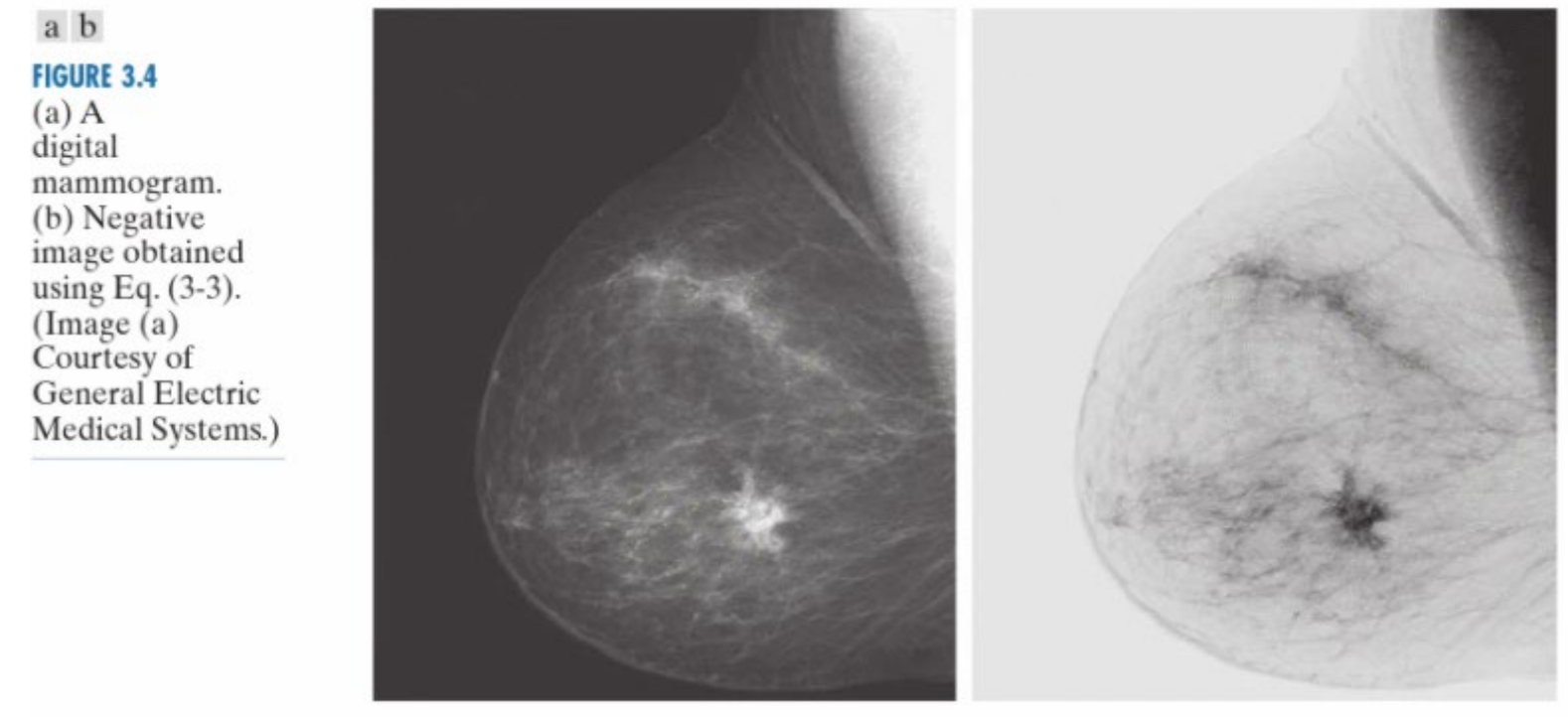
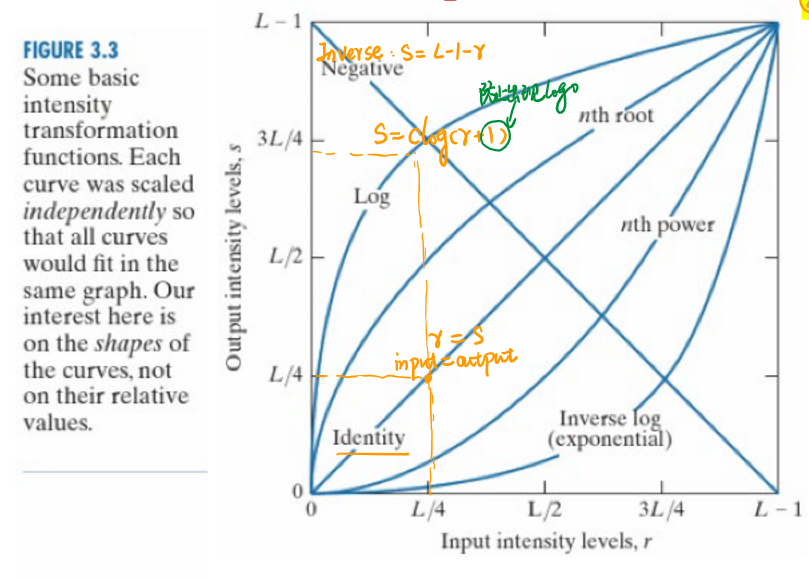
• 对数变换
  对数变换的表达式为：
  \[s=clog(1+r)\] 对数变换能够扩展低灰度值（突出过暗区域的细节）而压缩高灰度值（突出过曝区域的细节），从而增强图像的清晰度。
  

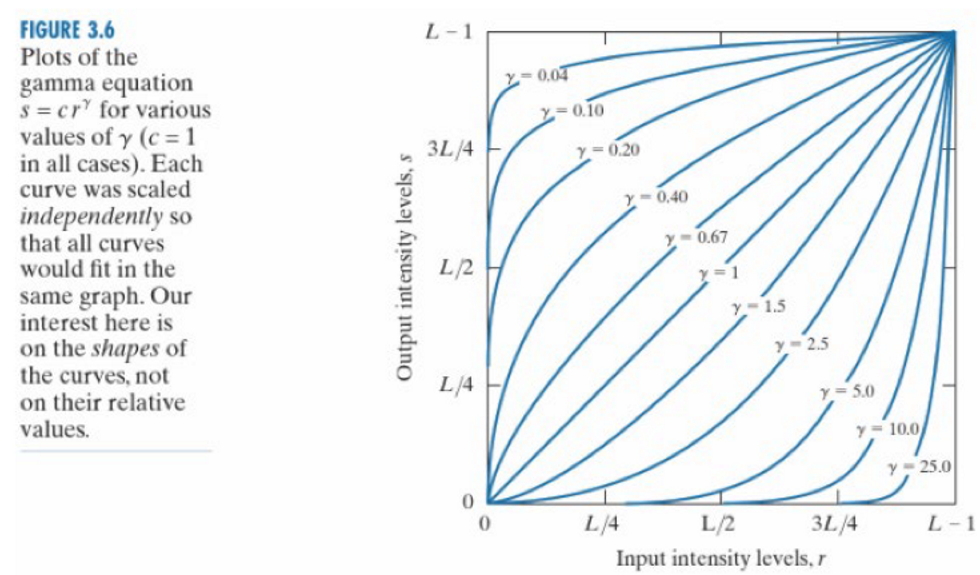
• 幂变换 \[s=cr^γ\] \(γ\)是幂指数，显示器中的伽玛校正(Gamma Correction)即调整该值使得显示器整体偏亮或偏暗。 当\(0<γ<1\)时，显示器偏暗，\(γ<1\)时，显示器偏亮。
  
  

• 线性分段处理(linear piecewise)
  线性分段处理(linear piecewise)可以分区域对不同的灰度区域实现不同的映射，进而选择性地增强图像的细节。如下图例子中只有处于中等灰度值的像素被加强。
  

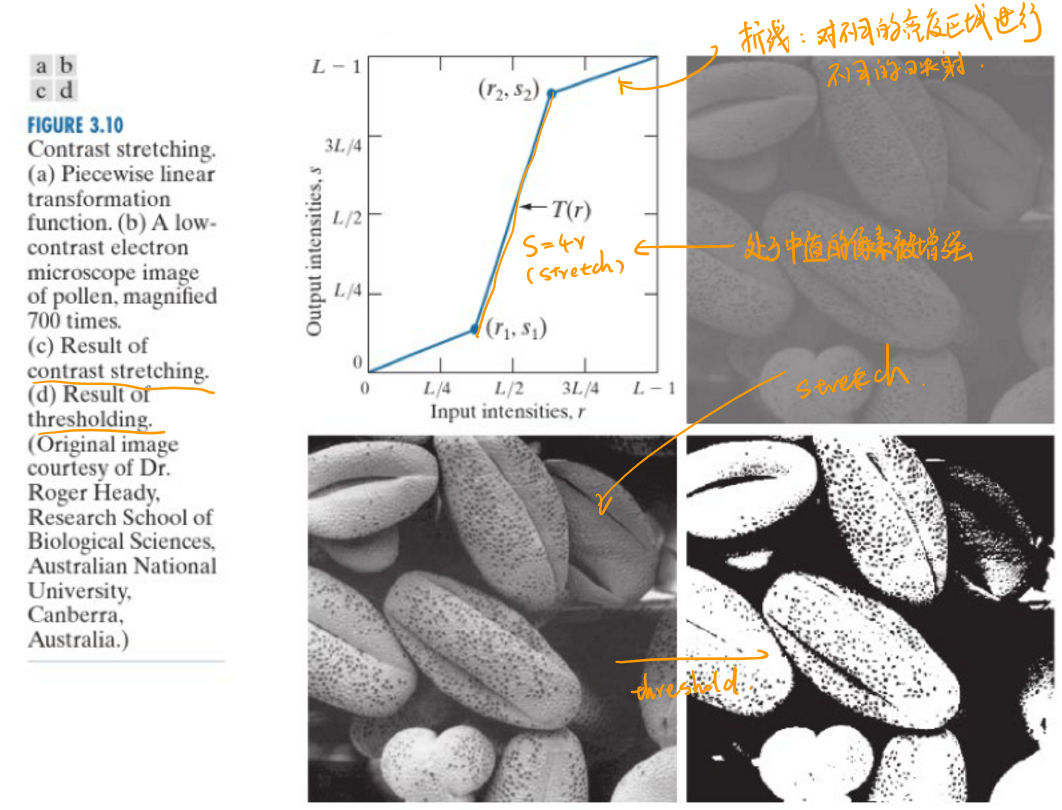
局部增强可以选择在增强目标灰度区域的同时减弱其他灰度区域的像素值，也可以选择让其他灰度区域的像素值保持不变。

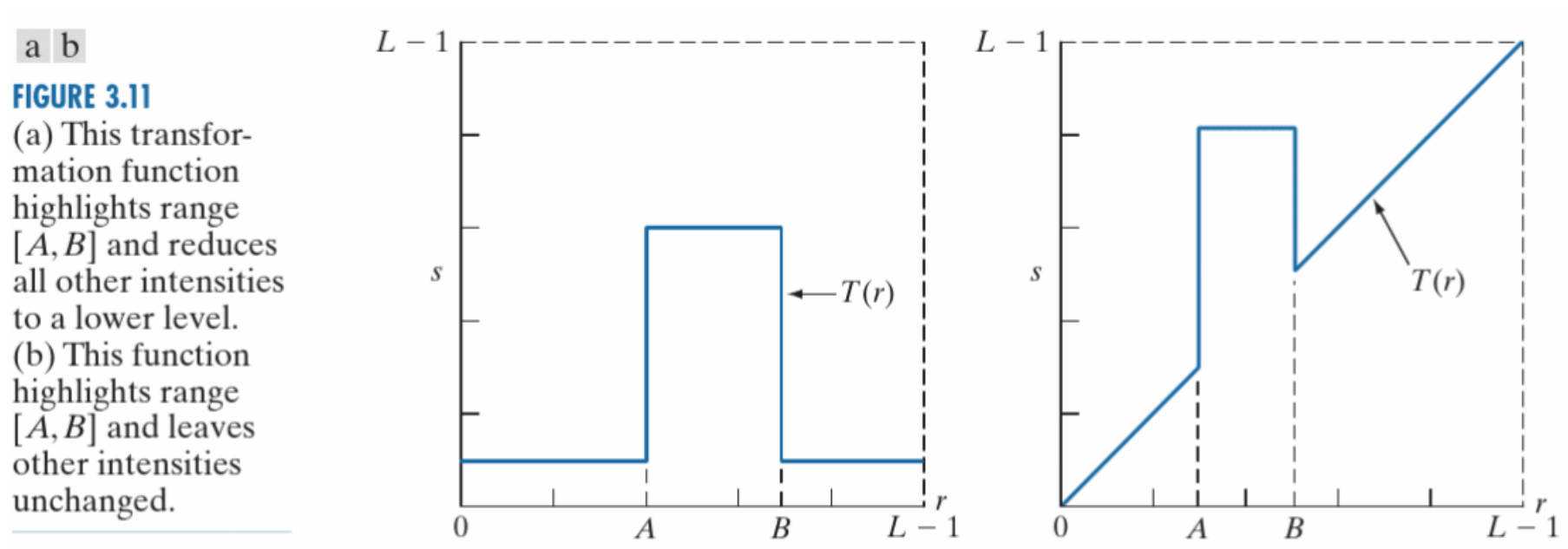
亮度直方图(Historgram)

亮度直方图的横轴是像素值，纵轴是该像素值内的像素点个数，它反映了黑白图像整体的像素分布情况。
如果直方图在白色区域内比较集中，图像偏亮，直方图窄黑色区域内比较集中，图像偏暗。

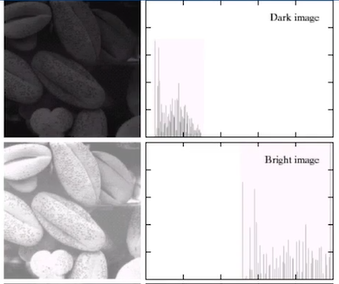
图像在直方图上的最大分布范围（即横轴的宽度）称为对比度(Contrast)，直方图窄的图像对比度低。通常情况下，对比度越高图像越清晰。

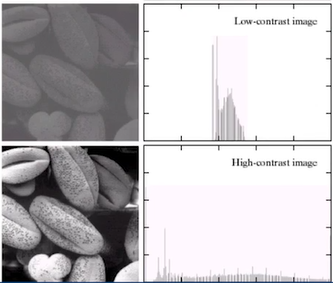
• 直方图均衡(Historgram equalization)
  直方图均衡是一种用于增强图像对比度的同时均衡图像亮度的方法（即拉宽和拖平直方图）。
  直方图可以视为反映了每一个像素值在整个图像的占比关系（\(\frac{n_w}{n}\)，n表示图像像素点总数，\(n_w\)表示像素值为w的像素点数量），因此整个直方图可以被概率分布函数化：
  \[p_r(w)=p(r=w)=\frac{n_w}{n},w=0,1,...,255\]
  应用变换：
  \[s=T(r)=(L-1)\int_0^rp_r(w)dw\] 使得:
  \[P_s(s)=P_r(r)|\frac{dr}{ds}|=\frac{1}{L-1}\]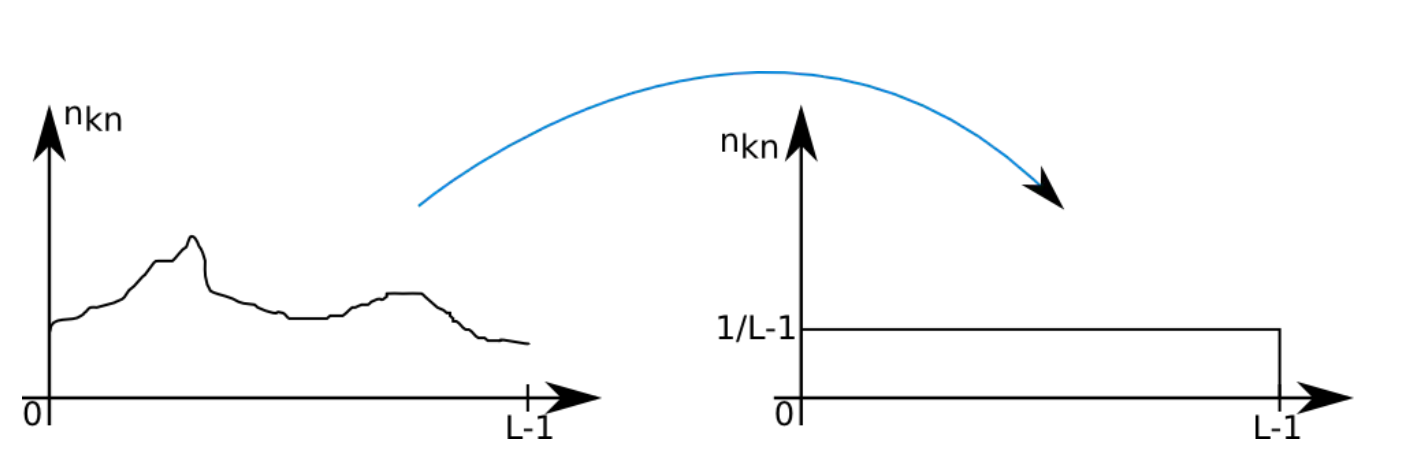
  由于w并不是连续的，因此最终的直方图并非是完全扁平的矩形。
  
• 局部增强(Local enhancement)
  对局部的一些像素群（例如以某个像素为中心\(9 × 9\)或\(3 × 3\)的像素）应用直方图均衡的方法称为局部增强。
  

相邻处理（Neighborhood Processing）

与点处理比较，虽然相邻处理的输入值仍然是一个像素值，但是输出值确实一个围绕输入像素值的像素集。（如下图所示）

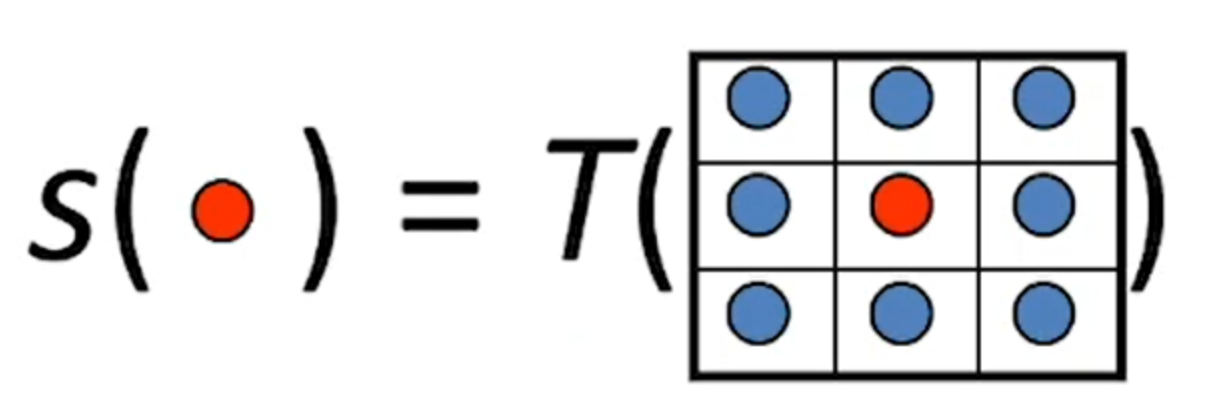
常见的一些相邻处理的方法：
- 均值滤波
- 最值滤波
- 中值滤波（像素值按大小排列，取排序位于中间位置的像素值作为中值滤波后的像素值）

▲上面的三张图依次是：原图（有一些细小噪点）、求平均、求中位数后的输出。

滤波（Filtering）

滤波是一种应用于相邻处理的常见方法。
设以某个像素为中心的像素方阵称为核矩阵(Kernel/Mask matrix),以\(W\)记，核矩阵中的每一个像素值以\(w(u,v)\)表示。 将核矩阵照射至图像的某一区域\(r\)，使被照射区域中的像素值与对应的核矩阵中同位置的像素值一一相乘后全部相加，最后用一常数\(C\)调整，该过程被称为滤波。
\[s(x,y)=C∑_{(u,v)∈W}w(u,v)r(x+u,y+v)\]
整个过程可以用下图来表示：

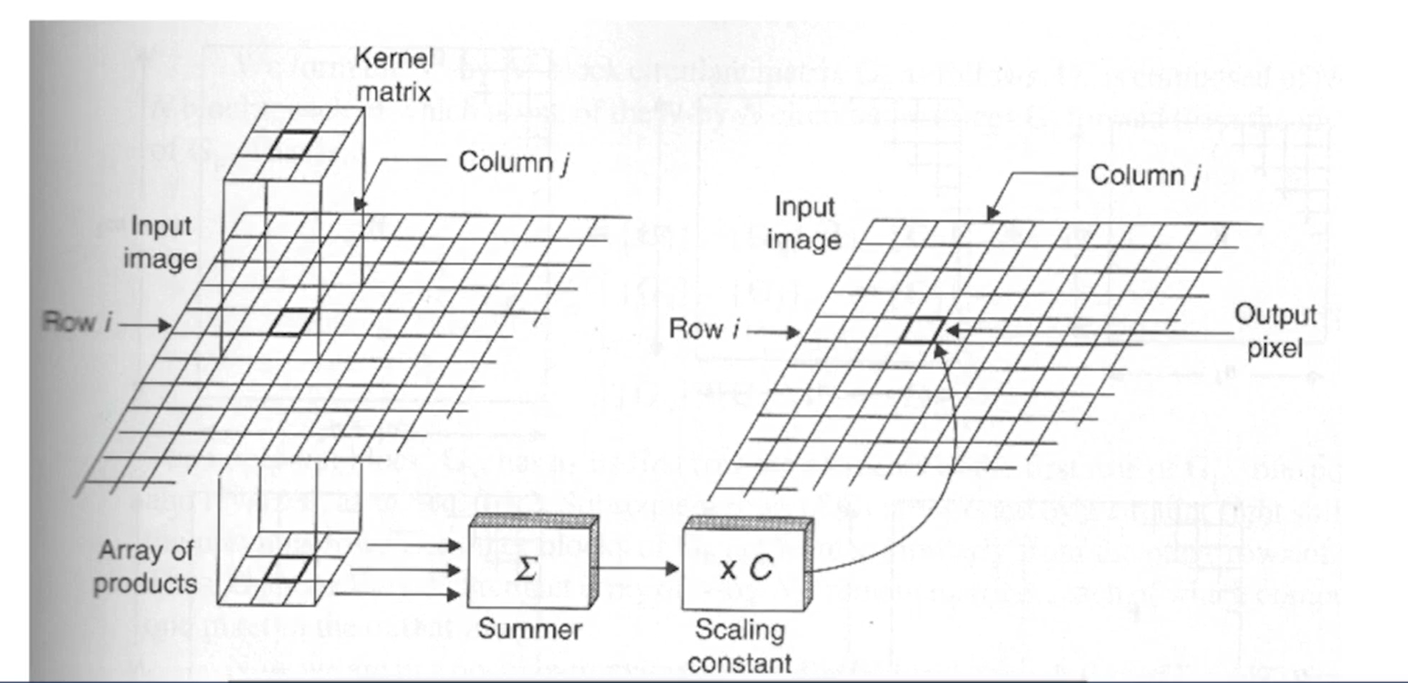
一次滤波结束后，核矩阵平移\(α\)个像素单位（称为步长(Padding)），照射图像的另一个区域，重复上述过程。

• 均值滤波
  其核矩阵如下：
  \[\frac{1}{n}×\begin{bmatrix} 1&1&...&1\\...&...&...&...\\ 1&1&...&1 \\ 1&1&...&1\end{bmatrix}\]
  n表示方阵元素的数量。
  这样最终的输出结果是取像素点周围领域的平均值作为响应输出，最终的图像会被模糊化。

• 高斯滤波(Gaussian Filtering)
  高斯滤波的核矩阵内的元素在三维上符合标准高斯/标准正态分布，且最高点在核矩阵中心处，如下图所示。
  
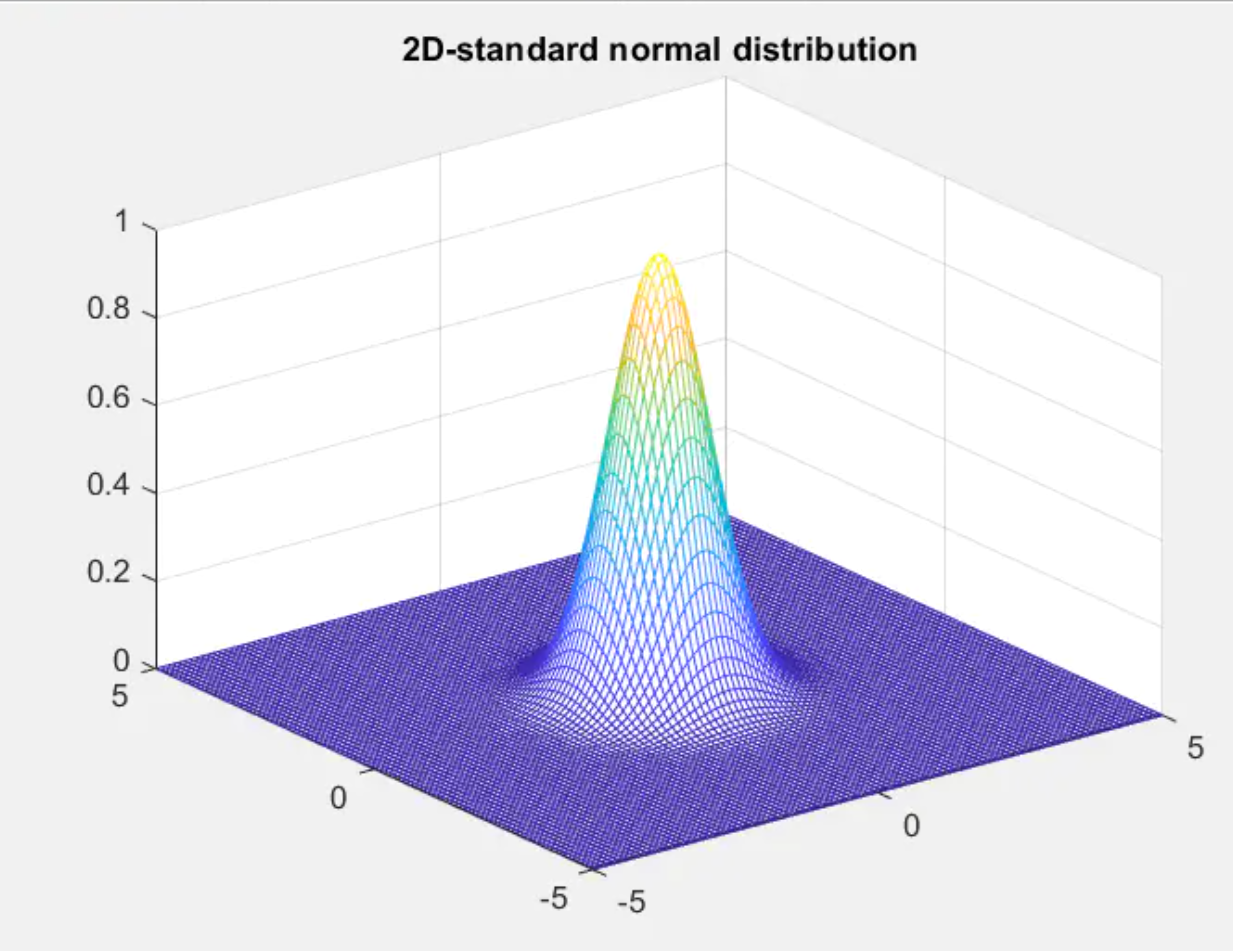
  其具体的计算公式为：
  \[G(x,y)=\frac{1}{2πσ^2}e^{-\frac{x^2+y^2}{2σ^2}}\]
  \(σ\)是标准高斯分布中的方差，\(σ\)较小时，图像的峰值窄且高。
  例如当\(σ=1.4\)时，其核矩阵可以取：
  
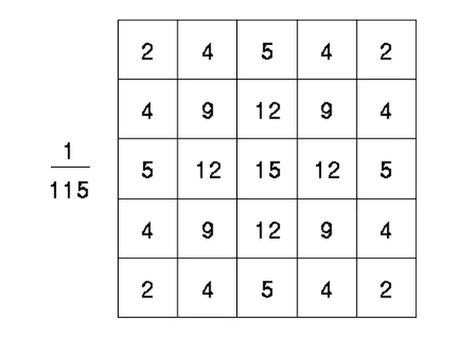
  高斯滤波的作用是将图像模糊化，使图像呈现一种毛玻璃的质感。运用高斯滤波处理图像的方法又被称为高斯模糊(Gaussian Blurring)。
  
  高斯模糊的重要作用是将图像中的噪点通过模糊化图像的方法移除。

卷积

卷积(Convolution)是一种常用于图像处理的方法。 设核矩阵(又被称为卷积核)的像素分布可以表示为\(h\),原图的像素分布表示为\(f\)，卷积有如下公式： \[g(x)=\int_{-∞}^∞f(τ)h(x-τ)dτ\]

• 卷积核的正则化
  如果要使得图像的整体亮度在卷积前后不发生改变，卷积核必须被正则化，即卷积核内所有元素的和必须是1。

边缘检测

边缘（Edges）是图像中像素值变化急剧(Sharply)的部分，常见的边缘有如下图所示的四大类。

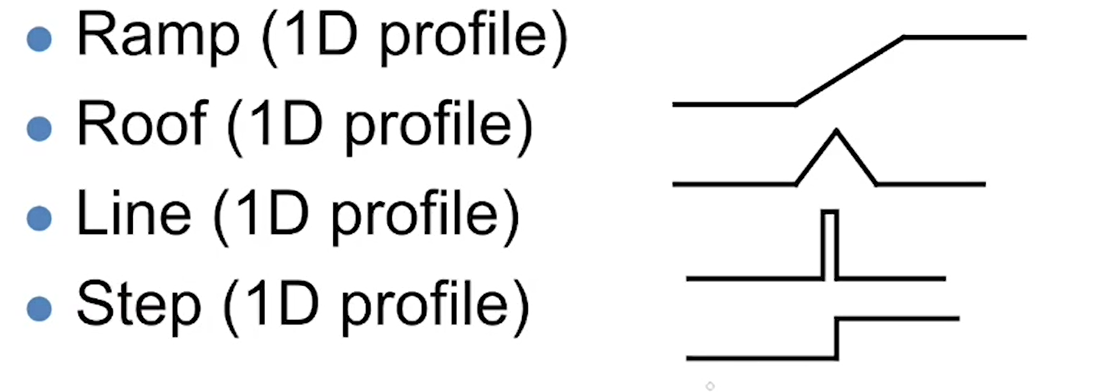
边缘检测是以特殊的卷积核（称为算子（Operator））对图像进行处理。
常见的算子有如下几种：
- Roberts算子
Roberts算子是两个能够强化图像的边缘部分的核矩阵： \[G_x=\begin{bmatrix} +1&0\\0&-1 \end{bmatrix}\] \[G_y=\begin{bmatrix} 0&+1\\-1&0 \end{bmatrix}\]

• 索伯算子(Sobel's Operator)
  Sobel算子的两个卷积核形式：
  \[\begin{bmatrix} -1&0&+1\\-2&0&+2\\-1&0&+1 \end{bmatrix}\] \[\begin{bmatrix}+1&+2&+1\\0&0&0\\-1&-2&-1\end{bmatrix}\] 两个卷积核的特征是卷积核正中的纵列或行列为0，用于检测图像的纵向/横向边缘。
  PIL或者是OpenCV中有对应的库可以执行Sobel边缘检测。
  

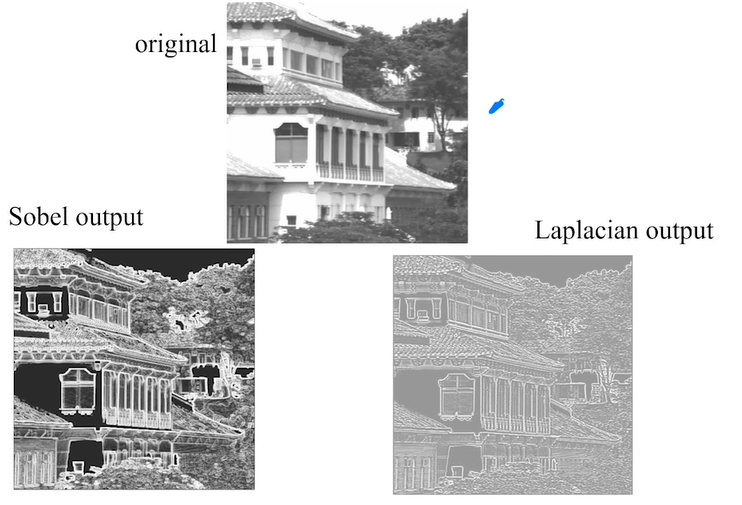
• 拉普拉斯算子(Laplacian operator)
  函数\(F(x,y)\)的梯度可由梯度公式得到：
  \[G(x,y)=\frac{∂F(x,y)}{∂x}cos(σ)+\frac{∂F(x,y)}{∂y}sin(σ)\]
  定义拉普拉斯算子（一阶）\(▿f|(x_0,y_0)=(f_x(x_0,y_0),f_y(x_0,y_0))\)，其二阶形式： \[▿^2f(x,y)=\frac{∂^2f(x,y)}{∂x^2}+\frac{∂^2f(x,y)}{∂y^2}\]
  在x方向上可以近似由差分表示：
  \[\frac{∂^2f(x,y)}{∂x^2}=f(x+1,y)+f(x-1,y)-2f(x,y)\] 在y方向上同理，最终得到二阶拉普拉斯算子的表达式： \[▿^2f(x,y)=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)\] 得到拉普拉斯算子的卷积核形式：
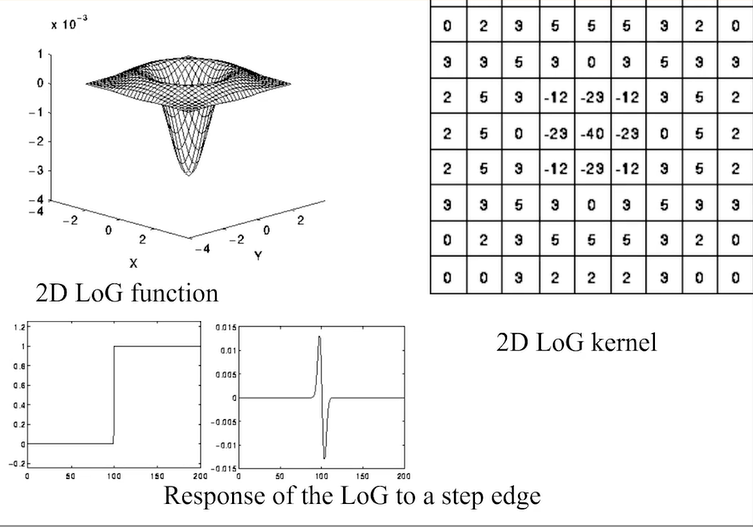
  \[\begin{bmatrix} 0&1&0\\1&-4&1\\0&1&0 \end{bmatrix}\]

• 拉普拉斯-高斯算子（LoG operator）
  由表达式：
  \[▽^2g(x,y)=-\frac{1}{2πσ^4}(2-\frac{x^2+y^2}{σ^2})e^{-\frac{x^2+y^2}{2σ^2}}\] 所得到的算子的卷积核形式：