4. 分类器

分类器

分类器概述

设\(S=\{ω_1,ω_2,..,ω_c\}\)是表示所有特征标签ω的集合，x表示数据集空间\(R^n\)中的特征向量，定义：分类器（Classifier）是一种能够使\(R^n→S\)的函数\(f\)。分类器能够将特征标签（labels）指定到特征向量。
- 图像识别的基本流程
输入图像—>预处理->获取特征->分类 ## 特征 特征(Features)是不同类别的数据具有的用于识别其自身的属性。在机器学习中，要想对数据集进行识别和分类就必须要提取数据集的特征。
特征的提取并不是越多越好，不相关的特征（称为噪声（Noise features））会降低识别的准确度；具有高相关性的特征（比如：长发和女性）会让模型出现过拟合（Generalization）和模型冗余之类的其他问题。
- 决策边界
决策边界（Decision boundary）是二元分类中能够依据特征的分布来分出两类的边界。

• 过拟合问题（Generalization）
  如果一个模型虽然可以穿过所有的数据点，但是其图像波动很大，其同样也不能描述数据的分布，（其数据的分布是无法被泛化处理），称为过拟合，或者说这个算法具有高方差的特性。
  

贝叶斯分类器

贝叶斯分类器(Bayes' classifier)被理论证明是目前最好的分类器。贝叶斯分类器依赖于模式识别(Pattern recognition)
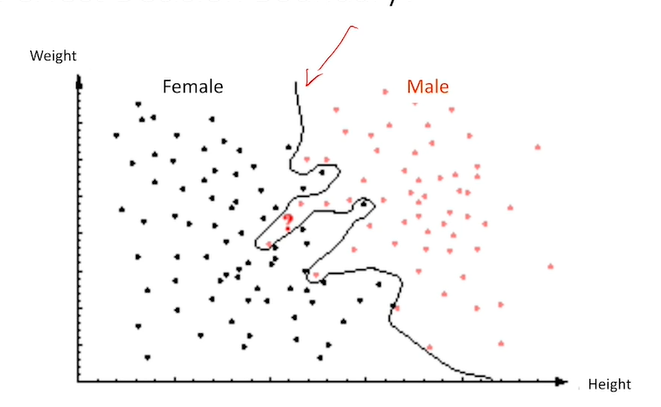
想象如下的情形：我们已经测量了用于识别男女性别的特征，现在要根据这些特征来对一个未知的人判断其性别。如果你对其不做任何的测量，那么你是否还能进行分类？
₋答案是：如果我们知道男女性别的比例，比如男性/总的人群:\(P{ω_1}=58.8%\)。将频率视为概率，那么这个概率被称为先验概率（Prior probability），由于是男性的概率大于是女性的概率，因此我们将这个识别目标总是判断为概率最高的标签——即男性，那么我们判断其为男性的正确率为58.8%。
如何去优化这个正确率？——对识别目标进行观测：
假设已经观测到目标的特征\(X\)，对标签集\(Ω\),计算所有的如果具有特性\(x\),识别目标为标签\(ω_i\)的概率，并从中找到最大的条件概率，目标特征的标签\(ω^*\)即为最大的条件概率。用数学公式表达为：
\[ω^*=arg_{ω_i}~maxP(ω_i|x)\] 由计算得出的概率\(P(ω_i|x)\)称为后验概率(Posteriori)。
由贝叶斯公式：
\[P(A|B)=\frac{P(B|A)×P(A)}{P(B)}\]
那么后验概率可以转化为： \[P(ω_i|x)=\frac{P(x|ω_i)·P(ω_i)}{P(x)}\]
带入分类器公式：
\[ω^*=arg_{ω_i}~max\frac{P(x|ω_i)·P(ω_i)}{P(x)}\] 由于\(P(x)\)是一个常数，那么最大值函数可以被简化为求\(P(x|ω_i)·P(ω_i)\)的最大值：
\[ω^*=arg_{ω_i}~maxP(x|ω_i)·P(ω_i)\] 这就是贝叶斯分类器公式。

• 特殊情况
  如果先验概率是均等的： \[P(ω_i)=P(ω_1)=...=P(ω_n)=C\] 那么分类器公式还能被简化为：
  \[ω^*=arg_{ω_i}~maxP(x|ω_i)\] 称为最大可能公式（Maximunm Likelihood）。

  如果分类器中只有两个标签\(ω_1,ω_2\):
  那么设定：
  \[g(x)=P(ω_1|x)-P(ω_2|x)\] 如果\(g(x)>0\)则判断为\(ω_1\),反之判断为另一类。\(g(x)\)称为判别函数（Discriminant function）。

• 代价/损失（Cost）
  设对于标签集\(\{ω_1,ω_2,...,ω_c\}∈C\),\(λ_{ij}\)是分类器判断为\(ω_i\)但实际上的标签是\(ω_j\)所作出的代价（Cost）。
  规定在\(λ\)中，当\(i=j\)时，\(λ_{ij}=0\)。
  那么二元的贝叶斯分类器的代价函数为：
  \[\frac{P(x|ω_1)}{P(x|ω_2)}>\frac{λ_{12}-λ_{22}}{λ_{21}-λ_{11}}·\frac{P(ω_2)}{P(ω_1)}.......ω_1\] \[\frac{P(x|ω_1)}{P(x|ω_2)}<\frac{λ_{12}-λ_{22}}{λ_{21}-λ_{11}}·\frac{P(ω_2)}{P(ω_1)}.......ω_2\] 如果\(λ_{12}=λ_{21}=1\)且\(λ_{11}=λ_{22}=0\),称\(P(x|ω_i)P(ω_i)\)为MAP方程。

贝叶斯分类器被证明是理论上误差最小的分类器。

运用贝叶斯分类器需要知道在有特征\(x\)的条件下是分类标签\(ω_i\)的概率——\(P(ω_i|x)\)，称为可能性（Likelyhood）。在实际运用当中，一般是从数据集中估计这个概率（采用抽样检测等方法），这个估计出的概率通常是不准确的。
这个抽样检测的原则是：如果要创建一个D维（D是特征向量X的维度，即特征的数量）的直方图，一般而言至少需要\(10^D\)的训练样本。

朴素贝叶斯分类器

解决贝叶斯分类器需要的训练样本数量大的问题的其中一个办法是假设所有的特征之间是独立的，根据概率论，有： \[P(XY)=P(X)P(Y)\]
假设特征向量\(x=[x_1,x_2,...,x_D]^T\)，有： \[ω^*=arg_{ω_j}~maxP(x|ω_j)P(ω_j)\] \[ω^*=arg_{ω_j}~maxP(ω_j)Π_{i=1}^DP(x_i|ω_j)\]
> 在实际中，由于\(P(x_i|ω_j)∈[0,1]\)，因此\(Π_{i=1}^DP(x_i|ω_j)\)的乘积可能会下溢（非常趋近0）。因此对两边取log函数将乘法项目转为加法项防止下溢。

\[ω^*=arg_{ω_j}~max~log[P(ω_j)]+∑_{i=1}^Dlog[P(x_i|ω_j)]\]
这种分类器公式称为朴素贝叶斯分类器（Naive Bayes）

K邻近算法

K邻近算法（K-Nearest Neighbor,KNN）是一种不依赖概率而直接求得决策边界的办法。

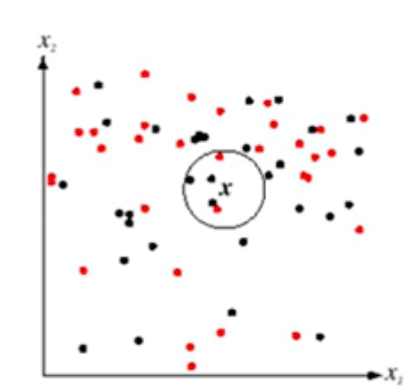
如上图，设想现在样本空间内有两类样本，新加入一个x到样本空间内，设定\(k=5\),计算x到样本空间内所有点的距离，最终取5个距离x最近的样本点，这五个样本点中哪一种类别的样本点多x就是哪一种类别。
通常情况下，标签数和K是都是奇数。
有数学证明在训练样本足够多的条件下， KNN的错误概率相比于贝叶斯更小。
\[P(error_{KNN})⪙P(error_{Bayes})\] - 距离度量（Distance Metrics）
设定距离度量函数\(D(x,y)\),具有非负性、唯一性、和三角矢量性。
\[D_p(x,y)=(∑_{i=1}^n|x_i-y_i|^p)^{1/p}\] x,y为向量。p称为范数（Norm）。
为了避免x，y的数值过于悬殊，人为地添加权重\(w_i\)，有：
\[D_p(x,y)=(∑_{i=1}^nw_i|x_i-y_i|^p)^{1/p}\]

其他分类器

• 神经网络 神经网络是目前最热门的分类器方法，它模拟了神经元的传递过程，即输入信号——处理信号——接收信号。
• 向量机（Support vector machine,SVM）
  向量机的目的是为了找到一个线性的决策边界。
  

性能评估

现在要对一个分类器的效果进行评估，方法是用另一组数据集去测试分类器的性能。在实际运用中，通常把训练集划分为两部分：训练集和测试集。 测试集不会被训练。 将测试集放入分类器后，分类器得出的标签和测试集中的标签进行对比。
### 混淆矩阵
有如下将测试结果可视化的方法，称为混淆矩阵(Confusion matrix)方法：
将横轴作为实际的标签，纵轴作为预测的标签，每一格表示“实际为标签i/但是预测为标签j”的频率，做出矩阵，如下图所示：

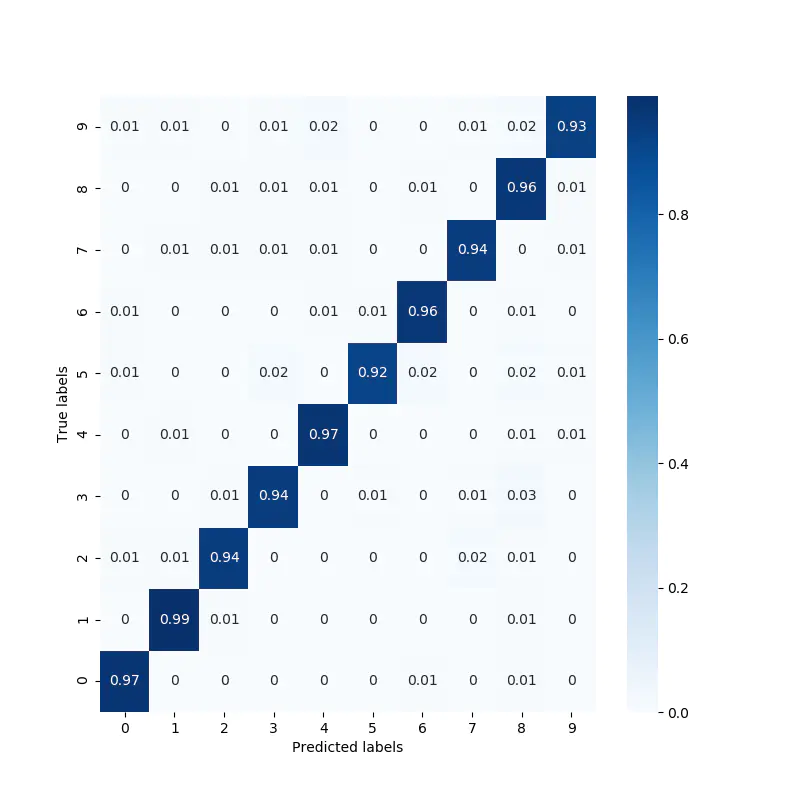
对角线上频率的总和即为训练集的正确率。
混淆矩阵能够容易的表现出分类器错误的分类情况。

交叉验证

交叉验证（K-fold cross validation）能够最大程度的避免测试集发生的“偶然正确（称为福禄克测试，Fluke test）”，具体的做法是：
将数据集平均分为k份，取其中一份为测试集，剩下的为训练集。重复上述步骤直到每一份都被做过训练集。 最终分类器的准确率为所有测试的准确率的平均值。

错误类型与ROC曲线

• FRR
  False Reject Rate， 表示目标正确却识别为错误的概率。

• FAR
  False Accept Rate， 表示目标错误却识别为正确的概率。

• FTE
  Failure to Enroll Rate, 无法识别的概率。

理想条件下，FRR和FAR都应该等于0。不断地改变分类器的阈值，将横轴为FAR,纵轴为1-FRR，作出ROC曲线(受试者工作特征曲线, Receiver operating characteristic curve)。这条曲线始终在y=x以上。

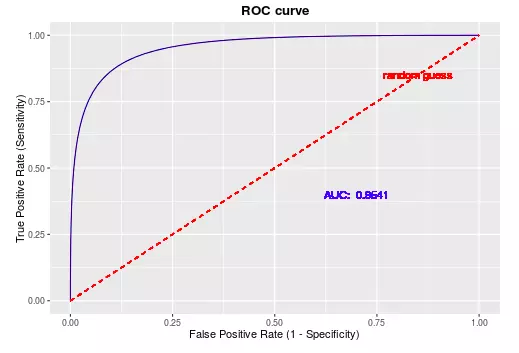
理想条件下，ROC曲线应该是一个倒L形状，即FAR=FRR=0，如下图所示：

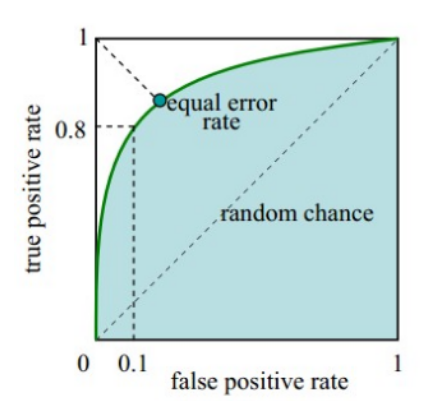
ROC曲线围成的下夹面积，即AUC表示了系统的强壮性(robust)，AUC越大越好。
EER(Equal error rate)，也就是FPR=FNR的值，由于FNR=1-TPR，可以画一条从（0,1）到（1,0）的直线，找到直线与ROC曲线的交点。 交点越靠近(1,1)越好。