5. 特征

特征

特征的选择

曾在第四讲中提到过特征的选择，特征的选取可以从颜色、形状、直方图等等来提取。
好的特征应该具有如下的性质：
- 计算简便 - 鲁棒性 - 储存小 - 好的区分度 - 更优的距离度量
### NP hard！ 尝试试所有的特征组合是一种在直觉上认为的简便方案，它是一种非确定性多项式(Non-Deterministic polynomial Hard，NP hard)问题，该问题在理论上能够用一种称为贪心算法(Greedy approach)的方法尝试解决：
- 对于F 个可能的特征，选择其中能给出最高准确率的一个特征X - 对于剩下的 F-1个可能的特征，选择与特征X组合能够给出最高准确率的一个特征。 - 重复上述过程，直到选择出所有的特征。

PCA

主成分分析（Principal Component Analysis，PCA）是另一种选择出更好的一组特征的方法。
设\(y ∈ R^k\)是图像(或者上一级的特征向量)\(x ∈ R^d\)的特征向量，\(k<<d\)，有：
\[y=W^Tx\]

• \(W\)
  \(W\)是一个\(d × k\)的正交矩阵，由x计算得到。
  设均值矩阵\(E[x]=0\),协方差矩阵\(E[xx^T]=C_x\),如下是计算\(W\)的方法：
  设回复向量（recovered vector）\(x_r=Wy\),误差\(ε =x-x_r=x-WW^Tx\), \[\begin{aligned} |ϵ|^2 & = ϵ^Tϵ \\ & =(x-WW^TX)^T(X-WW^Tx) \\ & =x^Tx-x^TWW^Tx-x^TWW^Tx+x^TWW^TWW^Tx \\ & =x^Tx-x^TWW^Tx \end{aligned}\] 令\(k=1\),此时\(W\)是一个向量: \[\begin{aligned} E[ ϵ^Tϵ] & =E[x^Tx-x^Tww^Tx]\\ & =E[x^Tx]-W^TC_xW \end{aligned}\] 那么需要找到使得\(E[ ϵ^Tϵ]\)最小的\(w\)，这一步与求\(max_w w^TC_xw\)等价。
  设\(J=\frac{w^TC_xw}{W^TW}\)以正规化W：
  令\(\frac{dJ}{dw}=0\)，得到： \[\frac{2C_xw}{w^Tw}-[\frac{w^TC_xw}{w^Tw}]·\frac{2w}{w^Tw}=0\] \[C_xw=Jw\] 这个公式正好是协方差矩阵\(C_x\)的特征值方程公式，即:\(w\)为协方差矩阵\(C_x\)的特征向量，\(J\)是它的特征值。

  如果对\(C_x\)进行特征分解(Eigen composition),得到一组特征值，将特征值从大到小排序，从中选取k个最大的特征值所对应的特征向量，组成矩阵\(W\)。
  \[W=[w_1 |w_2 |...|w_k]\]
  w称为主成分，所有的主成分两两正交。
  最终得到的PCA是：
  \[y=W^T(x-E[x])\] PCA将依据数据的分布，改变样本空间的坐标原点和坐标轴（表示原来的特征），并将所有的坐标轴变更为主成分，如图所示：
  
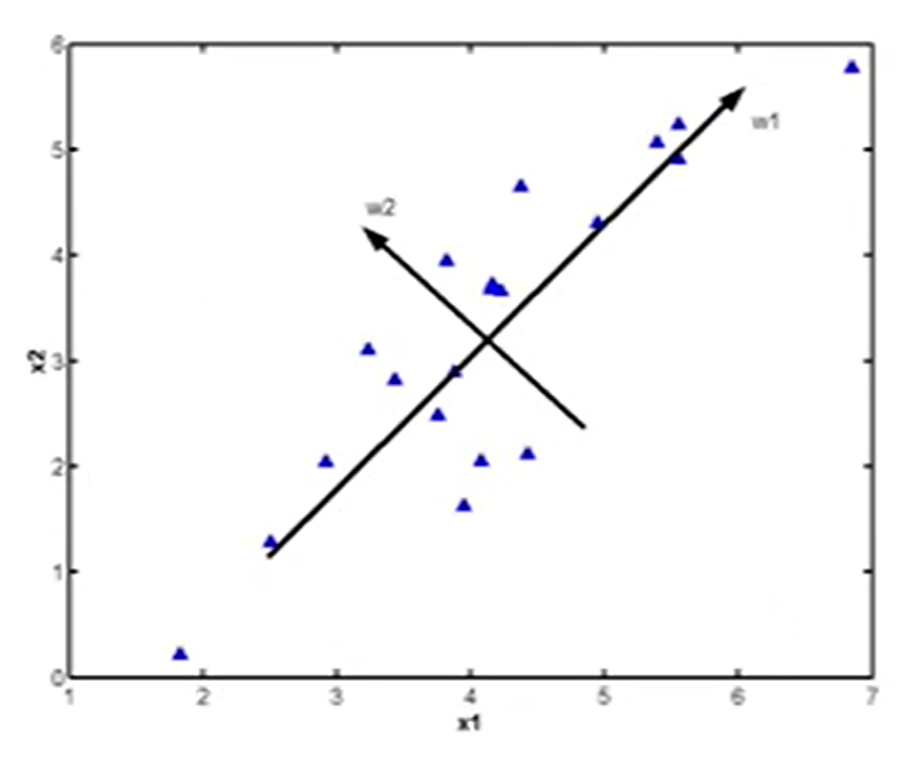
  y事实上是x的压缩集，改变后的y中的元素都是不相关的。

整个PCA过程中，k的选取十分的重要，通常k的选取遵循如下的规则：
记 \(λ\)是\(C_x\)特征分解后得到的从大到小特征值，有:
\[\frac{∑^kλ_i}{∑^dλ_i}≈90\%\] 即前k个特征值的和大约是总的特征值和的0.9左右。

• 案例
  1990年 Turk 和 Pentland应用PCA算法对人脸图像进行处理，称为特征子脸技术。特征子脸技术的基本思想是：从统计的观点，寻找人脸图像分布的基本元素，即人脸图像样本集协方差矩阵的特征向量，以此近似地表征人脸图像。这些特征向量称为特征脸(Eigenface)。