1.4. 优化和调试方法

优化和调试方法

特征缩放

对于某些不具有比较性的样本特征\(x_i\) （比如对其他的x来说\(x_i\) 相当大或者相当小），梯度下降的过程可能会非常漫长，并且可能来回波动才能最后收敛到全局的最小值。

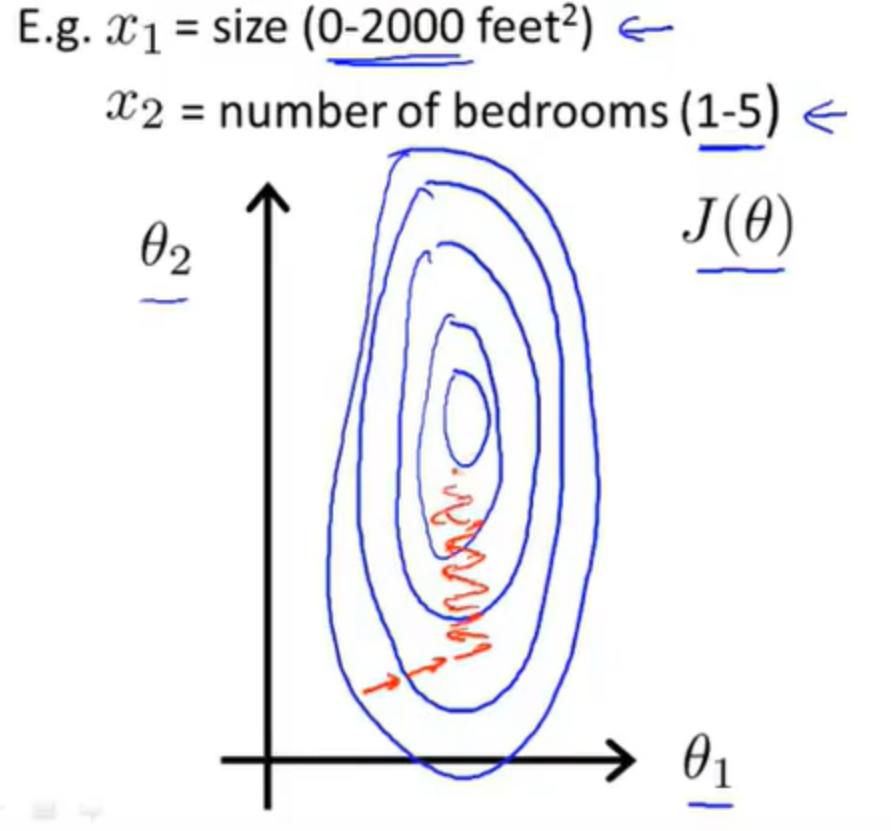
在这样的情况下，可以对\(x_i\) 进行缩放（如 \(x_i≔αx_i\) 或者 \(x_i=x_i/α\)），使得\(x_i\) 与其他的\(x\)具有可比性，以增加梯度下降的效率。
通常将\(x\)缩放至[-1,1] 的区间内。（只表示一个大致的范围，这不是绝对的。）

均值归一化

将\(x_i\) 替换为\(x_i−μ_i\) 使得特征值具有为0的平均值（对\(x_0\) 不适用） \[x_i:=(x_i−μ_i)/s_i\] 定义\(μ_i\) 为训练集\(X\) 的平均值，\(s_i=|x_imax−x_imin |\), 表示\(x_i\) 的取值范围（近似值），或者直接设置为\(s_i\) 的标准差。

学习率(Learning rate)

有如下的两种方法可以判断梯度下降算法是否已经处于收敛： 1. 绘制\(min_θJ(θ)-batch\)的图像
以迭代次数为横轴，以此时使得\(J(θ)\)局部最小时\(θ\)的值（即\(min_θJ(θ)\)）为纵轴绘制图像。

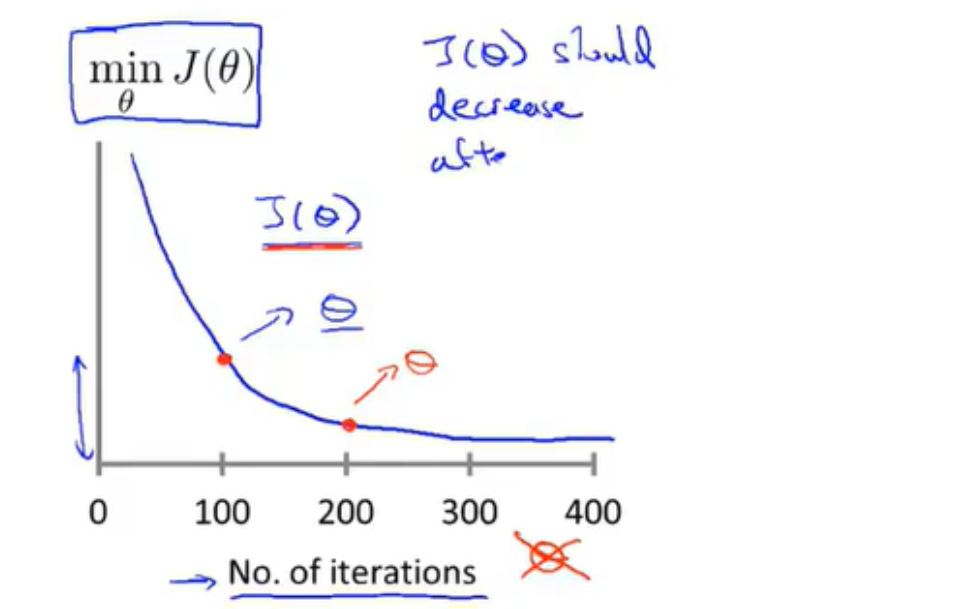
这样的做法需要在固定的迭代周期（比如每迭代100次穿插）时暂停学习，并求得此时的\(θ\)，然后绘制图像。
原则：在固定的迭代周期之后\(θ\)的值都应该减小，这样的图像能够通过直观地表现变化率来表现梯度下降是否收敛（变化率为0）。

2. 自动收敛测试
   如果\(J(θ)\)在某一次迭代之后的下降值小于某个设定好的阈值\(ε\)后，就能够判断算法已经达到了收敛。
   \(ε\)的设定具有技巧性，所以通常采取1.中的方法进行观测。

常见问题

常见的α过大的\(min_θJ(θ)-batch\)的图像：
- α过大，训练过程出现不稳定的振荡，甚至导致代价函数无法收敛。

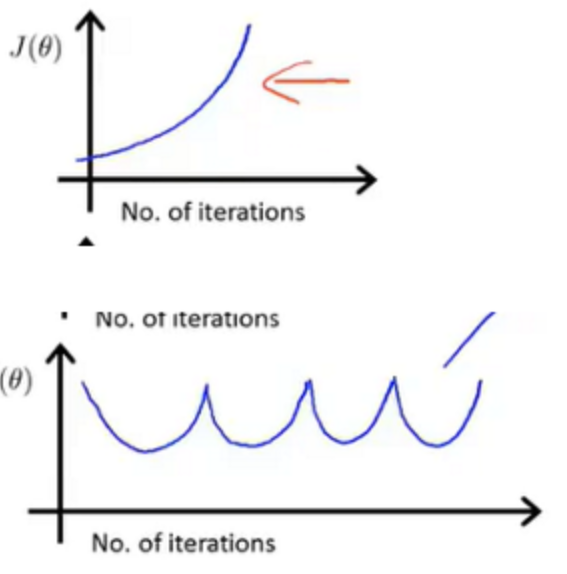
• α过小，导致代价函数收敛速度过慢。