6.2. 方差与偏差

方差和偏差

判断方法

运行一个学习算法时，如果模型表现不理想，有高可能性是发生了欠拟合（高偏差（Bias））或者过拟合（高方差（Variance））问题。 那么如何判断算法究竟出现了哪一种问题？
上一讲中已经定义过训练，测试和验证误差。 通常情况下，假设多项式模型中多项式的次数与训练和测试、验证误差的关系如下图所示：

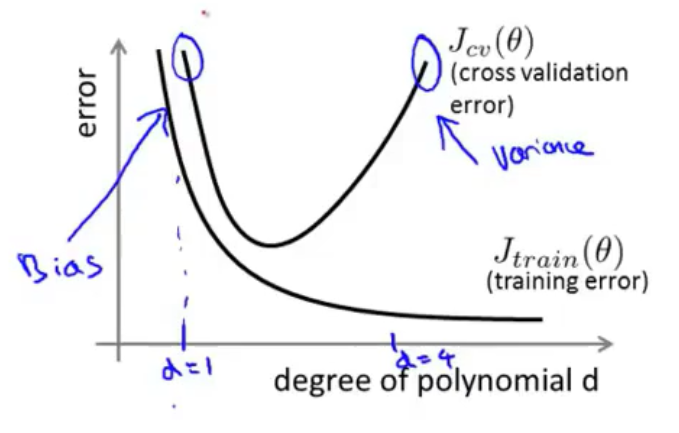
通过上图能够判断模型到底出现了欠拟合还是过拟合： 如果训练和测试误差都很高，那么有高概率是发生了欠拟合问题。 如果训练误差低，测试误差高（远大于训练误差），那么有高概率发生了过拟合问题。

偏差和方差与正则化算法

假设已经得到了一个\(d=4\)的多项式模型： \[h_θ(x)=θ_0+θ_1x+θ_2x^2+θ_3x^3+θ_4x^4\] 对其代价函数增加一个正则化项使得参数尽量缩小:
\[ J_{\theta}=\frac{1}{2m}[\Sigma_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})^2+λ\Sigma_{j=1}^{m}\theta_j^2]\]

下图表示了正则化系数\(λ\)的大小与拟合情况的关系：

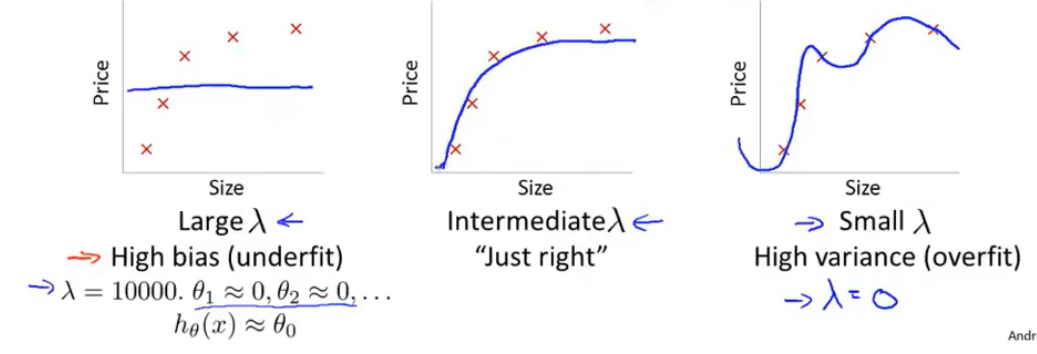
过大的\(λ\)容易发生欠拟合问题，而过小的\(λ\)（近似于\(λ=0\)）则无法起到规避过拟合的作用。
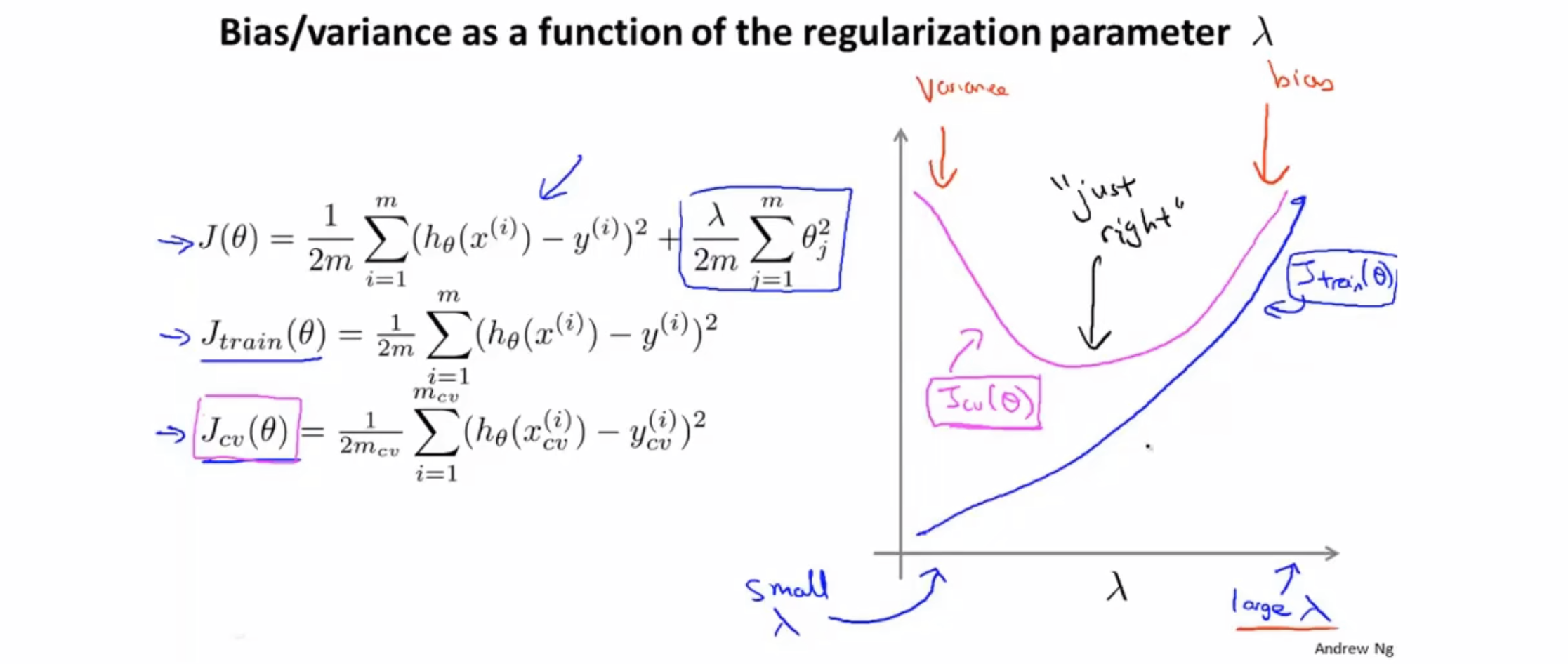
如何设置合适的\(λ\)呢？ 通过正则化的代价函数\(J(θ)\)求出最合适的一组\(θ\)，此时模型的训练误差\(J_{train}(θ)\)应当不包含正则化项，也就是： \[J_{train}(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_θ(x^{(i)})-y^{(i)})^2\]
在加入正则化算法后，测试一系列的\(λ\)的值，并得到一系列最优化的代价函数，并求到一系列的\(Θ\),再用验证集计算验证集误差\(J_{cv}(θ)\),最终选择验证集误差最小的那一组\(θ\),使用测试集计算出测试误差\(J_{test}\)。
下图表示了\(λ\)的大小与训练误差和验证误差的关系：