6.3. 学习曲线

学习曲线

学习曲线是一种检查算法是否正常运行的方法。 具体方法如下：
改变训练样本的总数\(m\), 分别计算一系列的训练误差\(J_{train}(\theta)\)和交叉验证误差\(J_{cv}(\theta)\)。得到结论：如果训练样本的总数很小，模型往往能够很好的拟合，随着样本数的增大，假设模型的平均训练误差会逐渐增大。对于验证集，由于验证集当中的样本都是未被训练过的，在训练样本数很低时，模型的泛化程度不高，因此如果训练样本的总数很小时，假设模型的平均验证误差会很高，随着样本数的增大，平均验证误差会逐渐减小。如下图所示：

高偏差和高方差学习曲线

高偏差学习曲线

如果模型不能很好的拟合数据，即出现了高偏差。 在训练集总数\(m\)非常小时，训练误差非常大，随着随着训练集总数\(m\)的增大，验证误差会逐渐的减小，最终停留在一个较高的水平。 对于训练误差，随着训练集总数\(m\)的增大，训练误差误差会越来越大，最终趋近于验证误差。 因为模型的参数过少，因此最终验证误差和训练误差会非常的接近。

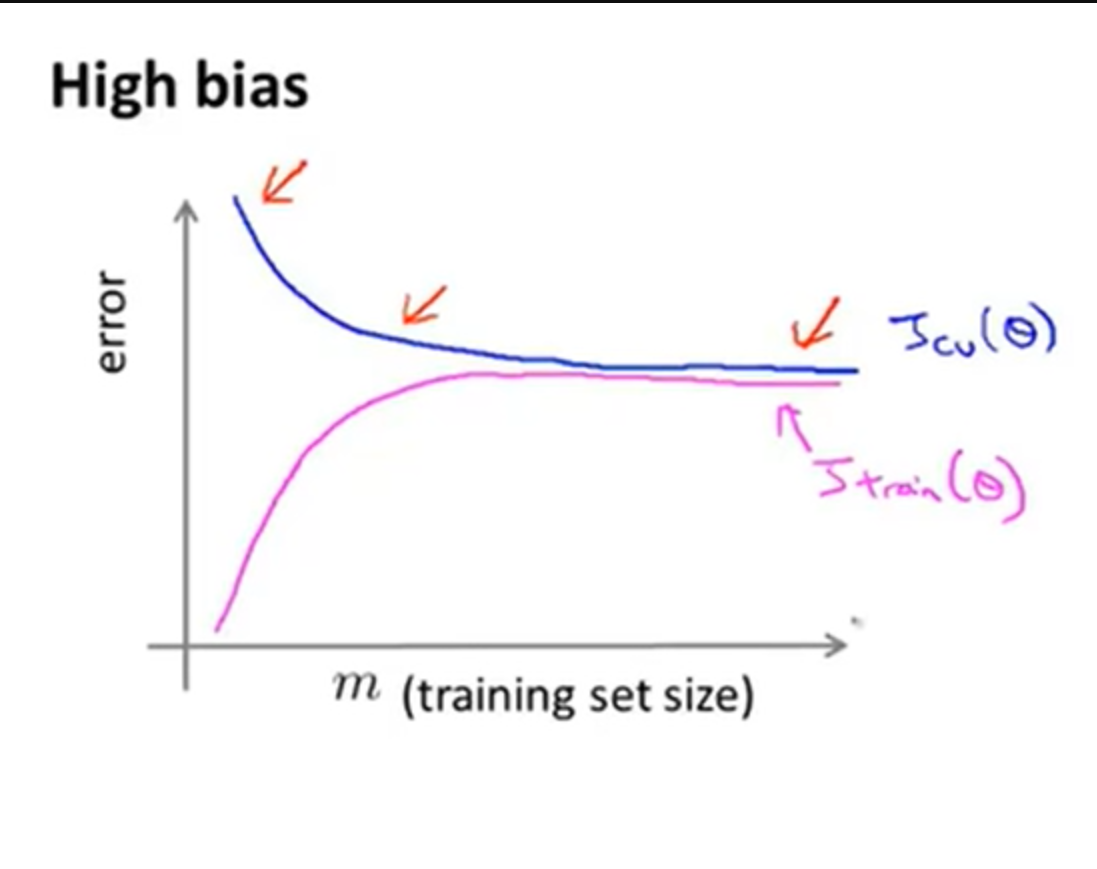
从上图可以看出：如果一个模型具有高偏差的特性，选用更多的训练集数据并不能改善准确度。
### 高方差学习曲线 模型在过拟合下，随着训练集总数\(m\)的增大，由于模型的泛化程度底下，因此训练误差会越来越高，并最终保持在一定水平。 同高偏差学习曲线一样，高方差模型的验证误差很大，并最终保持在一定水平。

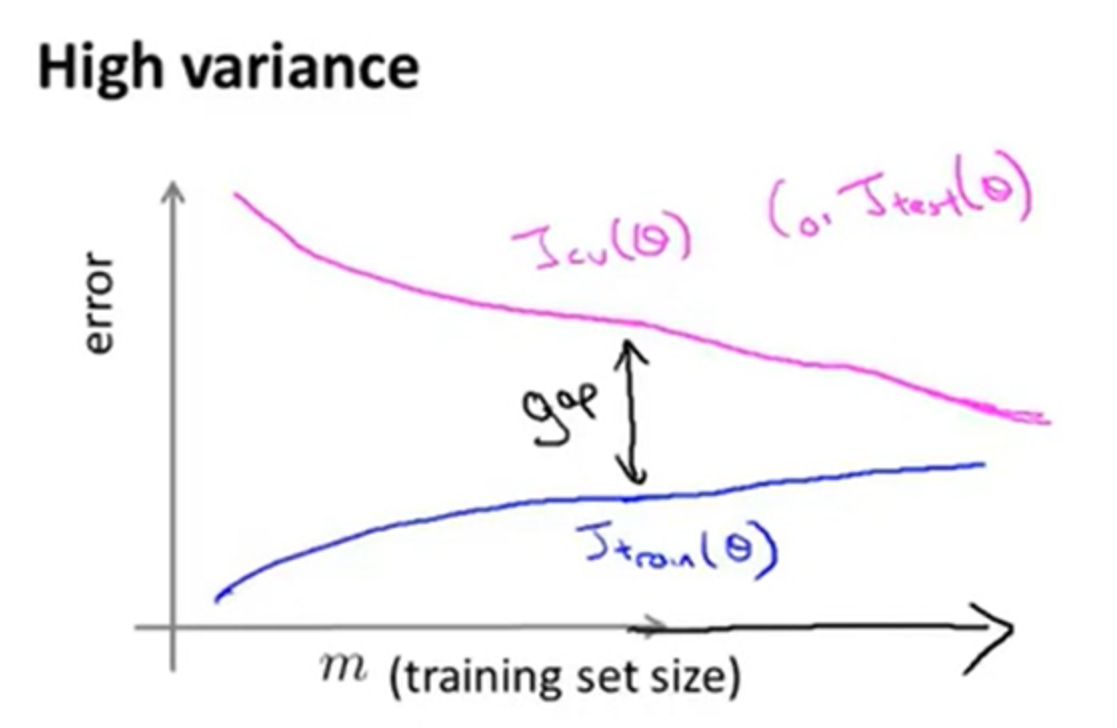
从上图可以看出：如果一个模型具有高方差的特性，选用更多的训练集数据能够改善准确度。