7.2. 查准率和召回率

查准率和召回率

偏斜类问题

在上一讲中提到了用一些数学指标来评估算法是非常有效的一种方法，但是如果错误地选用了某些指标就会导致偏斜类问题（Skewed Classification）的出现。
具体而言，对于癌症分类问题，如果训练了一个模型并用测试集检测出错误率为1%，但实际上测试集中只有0.5%的患者真正得了癌症。
这是因为在测试集中相比于正样本（不患癌症），负样本的比例太低，这就是偏斜类问题：即数据集中某一类样本的数量比其他类多很多，在这种情况下，机器学习算法甚至比“总是认为结果是该类”的算法准确度更低。在偏斜类的情况下，实验者无法判断高正确率（比如改动后的算法的准确度(Accurancy)只发生了非常细微的改动：从99.2%提升到了99.5%）究竟是由于类别不均衡还是算法本身造成的。
解决偏斜类问题的方法是引入新的数学指标：查准率(Precision)和召回率(Recall)。

查准率和召回率的定义

有如下将测试结果可视化的方法，称为混淆矩阵(Confusion matrix)方法：
将横轴作为实际的标签，纵轴作为预测的标签，每一格表示“实际为标签i/但是预测为标签j”的频率，做出矩阵，如下图所示：

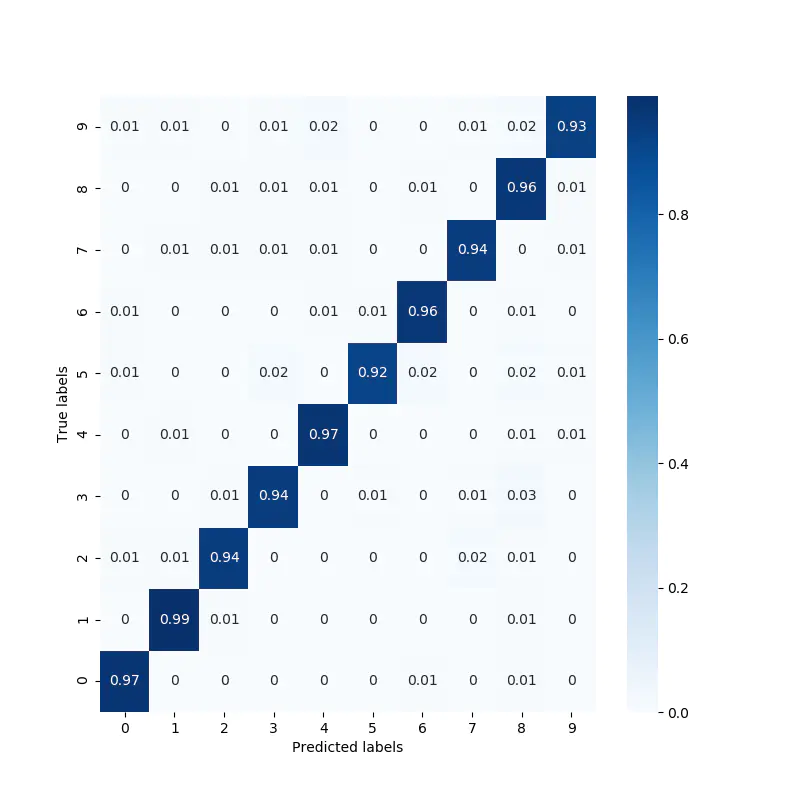
对角线上频率的总和即为训练集的正确率。
混淆矩阵能够容易的表现出分类器错误的分类情况。

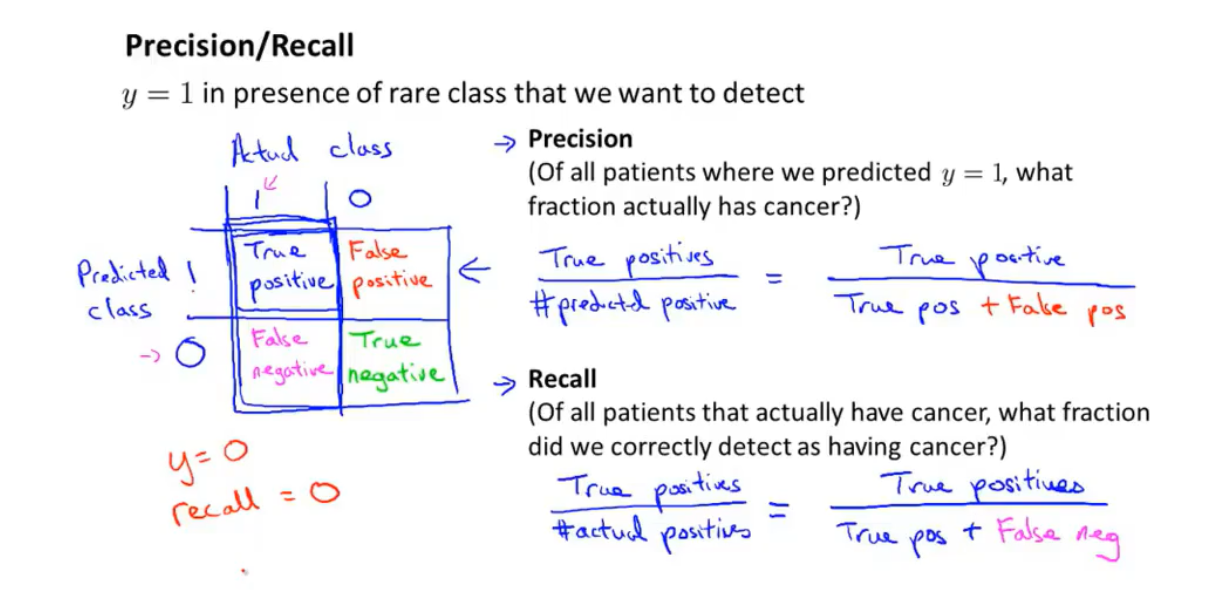
混淆矩阵可以得到查准率（P）和召回率(R)，具体定义为：
查准率=是阳性，预测为阳性的数目（真阳性）/预测为阳性=真阳性总数/（真阳性总数+假阳性总数）
召回率=是阳性，预测为阳性的数目（真阳性）/阳性总数=真阳性总数/（真阳性总数+假阴性总数）
用查准率和召回率检验“总是认为结果是该类”的算法，其召回率为0。

阈值、准确率与查准率和召回率

如果要想在非常确定的情况下才判断确证癌症，就需要对逻辑回归的阈值进行修改（比如\(h(x)\)大于0.9才判断为癌症），那么模型将具有高查准率，低召回率的特性，且模型的准确率很高。
相反，如果下降阈值（比如\(h(x)\)只要大于0.1就判断为癌症），那么模型将具有低查准率，高召回率的特性，且模型的准确率很低。
由此观之，以上的几个指标均与阈值的设定有关，那么如何通过准确率与查准率评价算法在不同阈值下的性能，从而决定阈值的取值？
基本的思路是将这两个指标转化为一个指标，从而更方便地对算法进行选择。 基本想法是用两者的均值替代这两者，但是极端情况（比如：极高召回率和极低的查准率）会让均值不能很好的反应算法的性能。 在这里介绍F值（或\(F_1\)值）:
\[F=2\frac{PR}{P+R}\]
F值能够给予两者中较低的值较大权重，因此F值越大，查准率和召回率越接近于1，算法性能越好。