8.1. 激活函数、代价函数和决策边界

激活函数、代价函数和决策边界

逻辑回归的代价函数的线性拟合

逻辑回归的激活函数：\(h(x)=\frac{1}{1+e^{-θ^Tx}}\)。
对于单个样本\((x,y)\)，逻辑回归的代价函数是：\(-ylog(h_θ (x))−((1−y)log⁡(1−h_θ (x)))\)，将\(y=1\)与\(y=0\)时的代价函数作出，并用线性进行拟合得到\(Cost_1(z)\)与\(Cost_0(z)\)（\(z=θ^Tx\)）两个线性的代价函数，两者的函数图像大致如此。

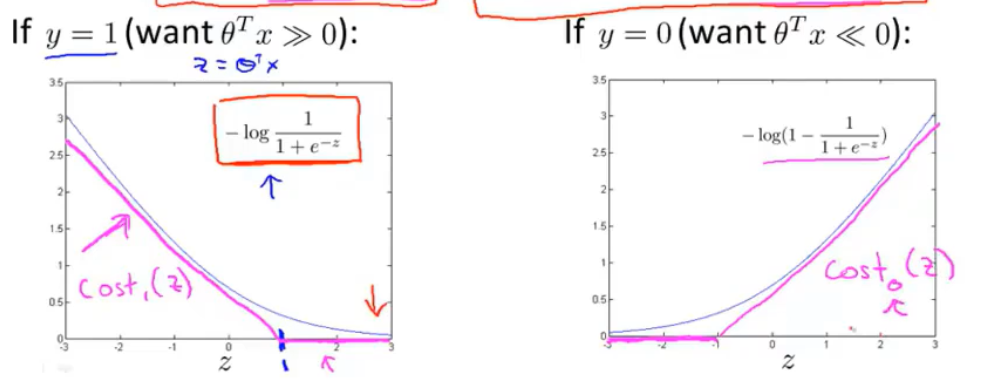
支持向量机是线性化的逻辑回归。

支持向量机的代价函数

逻辑回归的代价函数：
\[J(θ)=min\frac{1}{m}[∑_{i=1}^m y^{(i)} -log⁡(h_θ(x^{(i)} ))+(1−y^{(i)}) -log(1−h_θ (x^{(i)}))]+\frac{λ}{2m}∑θ^2\]
将\(-log\)项替换为如上图所示的两个线性函数：\(Cost_1(z)\)和\(Cost_0(z)\)，并去除\(\frac{1}{m}\)项（并不会改变最终结果） 得到支持向量机的代价函数：
\[J(θ)=min[∑_{i=1}^m y^{(i)} Cost_1(z))+(1−y^{(i)})Cost_0(z))]\]
在支持向量机中，通常通过给前项附加权重\(C\)而非给正则化项附加权重\(λ\)的方法来防止过拟合，得到正则化的支持向量机的代价函数：
\[J(θ)=minC[∑_{i=1}^m y^{(i)} Cost_1(z))+(1−y^{(i)})Cost_0(z))]+\frac{1}{2}∑θ^2\]

支持向量机的激活函数

与逻辑回归不同的是，逻辑回归的\(h(x)\)输出的是概率，而支持向量机的激活函数直接给出了预测的结果：
\[h_θ(x)=\begin{cases} 1, z>=0 \\ 0, otherwise \end{cases}\]

支持向量机的决策边界

> 原本只需要0作为阈值，但是为了保证SVM的精确度，因此将阈值选定为-1和1，这两个阈值间的距离称为安全间距。

如上图所示，如果\(y=1\)，需要\(z>=1\),反之如果\(y=1\)，需要\(z≦-1\)。
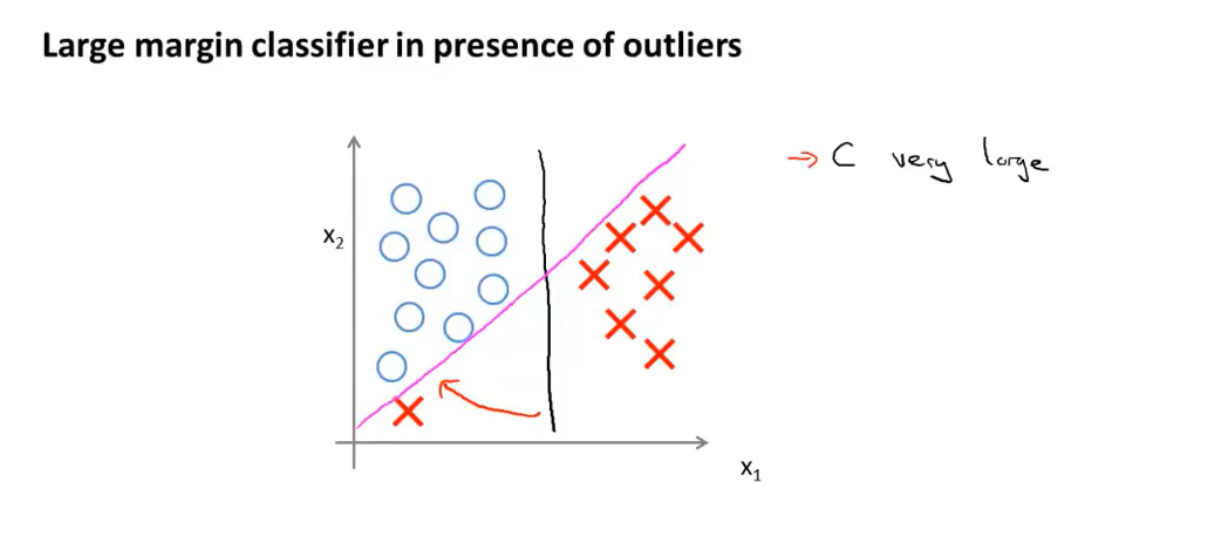
当SVM的代价函数前的权重值\(C\)非常大时：

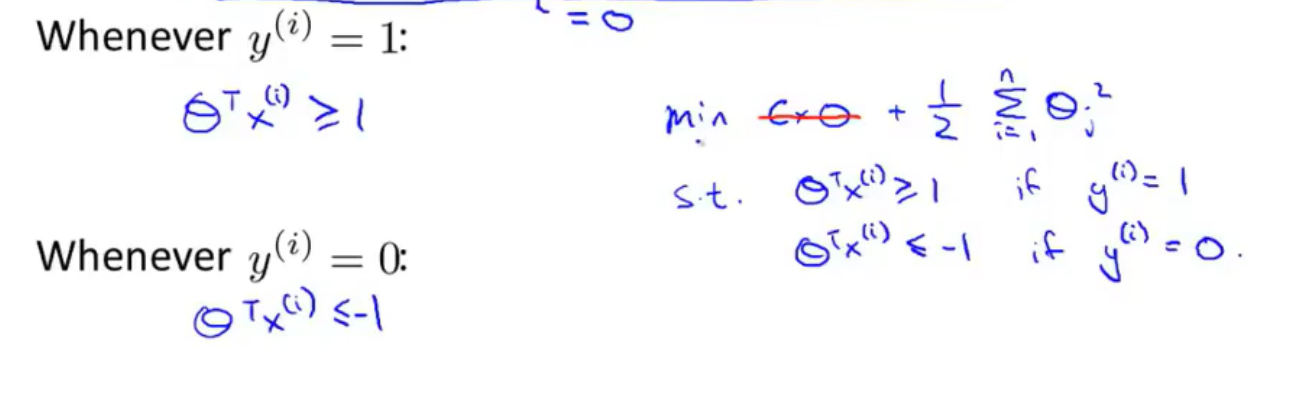
这为SVM创造了一个相当特殊的决策边界： 即在样本线性可分的条件下，SVM的决策边界是一条拥有与训练样本的最小距离的直线（图中黑线）。

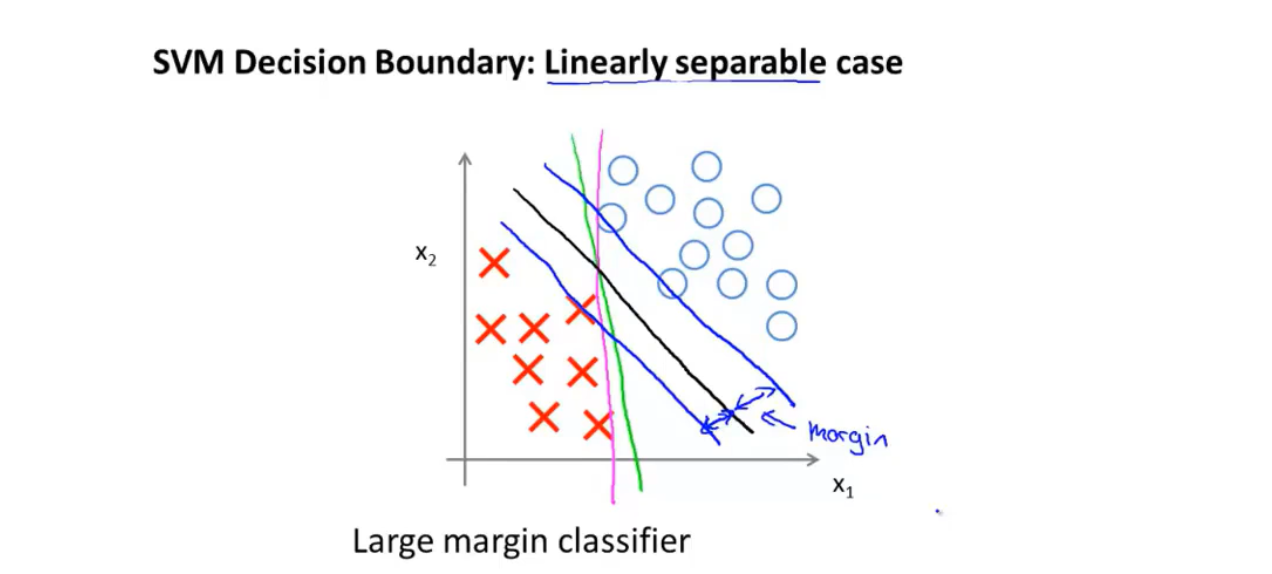
图中的蓝线表示了SVM决策边界与训练样本的间距。
因此支持向量机又被称为大间距分类器。
但是当正则化系数\(C\)被设置的非常大时，支持向量机的决策边界对异常数据非常的敏感，如下图的例子中所示。