8.2. 数学原理

数学原理

回顾：向量的点乘

对于向量\(u=[\begin{smallmatrix} u_1 \\ u_2 \end{smallmatrix}]\),\(v=[\begin{smallmatrix} v_1 \\ v_2 \end{smallmatrix}]\),定义向量的点乘为：\(u^Tv=||v||cosθ||u||\)。
其中\(||u||\)称为\(u\)的模长：\(||u||=√{u_1^2+u_2^2}\)；定义\(||v||cosθ=p\)，它是v在u上的投影。

优化函数的几何意义

对于svm的目标优化函数： 即存在\(min_θ\frac{1}{2}∑θ^2\),使得满足如果\(y^{(i)}=1,θ^Tx^{(i)}≥1\)，\(y^{(i)}=0,θ^Tx^{(i)}≤-1\)。
现在为了简化运算，假定\(θ_0=0\)，有且仅有两个参数，此时\(\frac{1}{2}∑θ^2=\frac{1}{2}(√{θ_1^2+θ_2^2})^2\)。
\(√{θ_1^2+θ_2^2}\)可以看做是向量\(Θ\)的模长，因此目标优化函数可以看做是0.5倍参数向量\(Θ\)长度的平方：
\[\frac{1}{2}∑θ^2=\frac{1}{2}||Θ||^2\]
现在来分析\(,θ^Tx^{(i)}\)的几何意义，按照向量的点乘法则，可以看做是向量\(x^{(i)}\)在\(Θ\)上的投影\(p^{(i)}\)与\(||Θ||\)相乘。
现在优化函数就可以表示成:
存在\(min_θ\frac{1}{2}||Θ||^2\)，使得：
如果\(y^{(i)}=1,p^{(i)}||Θ||≥1\)，
如果\(y^{(i)}=0,p^{(i)}||Θ||≤-1\)

现在来考虑svm对线性可分样本的分类：
如果决策边界与样本边界的间距很小，由于参数向量与决策边界是始终正交的，那么每一个样本到参数向量的投影\(p^{(i)}\)都很小，想要使得\(p^{(i)}||Θ||≥1\)或者\(p^{(i)}||Θ||≤-1\)就需要\(||Θ||\)非常的大。（下图左）
反之如果决策边界与样本边界的间距很大，那么\(||Θ||\)就可以小一些。(下图右)
因此决策向量机总是使得决策边界具有大间距的特性。

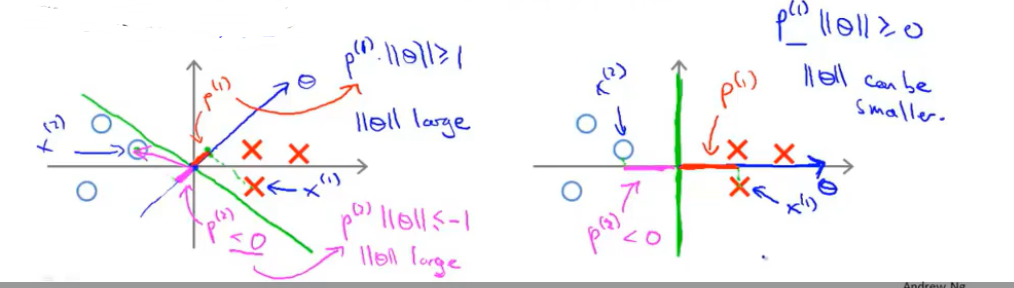
> 由于决策边界的上方有\({x^{(i)}}^T||Θ||>0\)，下方有\({x^{(i)}}^TΘ<0\),因此直线上必定有\({x^{(i)}}^T||Θ||=0\)。
> 因此参数向量与决策边界是始终正交的。