8.3. 核函数

核函数

非线性分类的SVM

本节将使用核函数对支持向量机进行改造，使其成为复杂的非线性分类器。

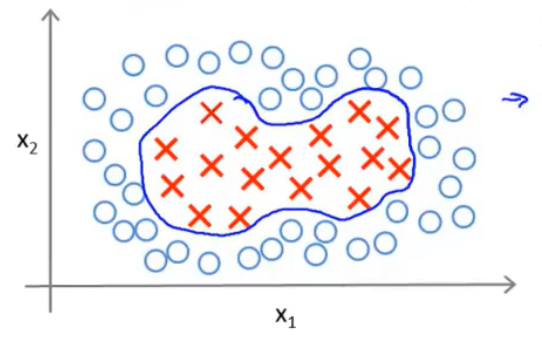
比如对于如上图所示的分类，决策边界是非线性的。 此时一种对其拟合的方法是用多项式对其进行拟合。
比如： 当\(θ_0+θ_1x_1+θ_2x_2+θ_3x_1x_2+θ_4x_1^2+θ_5x_2^2+..≥0\)时,预测\(y=1\)。
就能够得到一个假设函数：
\[h_θ(x)=\begin{cases} 1  \text{if} θ_0+θ_1x_1+..≥0 \\ 0  \text{otherwise} \\ \end{cases}\] 这种方法的问题是假设中的某些高阶项可能是冗余的，并且对于计算机视觉而言，用高阶多项式处理矩阵的计算量非常的大。
改进方法是用一些新的特征\(F=\{f_i\}\)来替换原特征\(X=\{x_i\}\)。
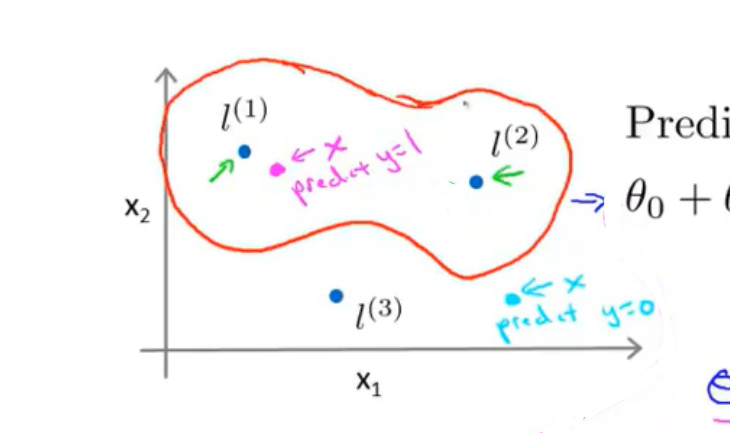
具体而言，比如现在只选取三个特征\(x_0\)（截距项，如下推导中将被忽略）,\(x_1\),\(x_2\),在这三个维度上手动选取三个点（称为标记（Landmarks））：\(l^{(1)}\),\(l^{(2)}\),\(l^{(3)}\)。
将新特征i \(f_i\)表示为训练样本\(x\)与\(l^{(i)}\)的相似度，相似度度量可以用如下公式表示：
\[Similarity(x,l^{(i)})=e^{-\frac{||x-l^{(i)}||^2}{2σ^2}}\] > 欧氏距离：空间中两点的连线距离，表示为\(d=√{∑x_i^2}\)。
> \(||x-l^{(i)}||\)表示空间中\(x\)与\(l^{(i)}\)的（欧式）距离。

这个相似度函数称为高斯核函数（Gaussian Kernel Function）。
\[k(x,l^{(i)})=e^{-\frac{||x-l^{(i)}||^2}{2σ^2}}\] 此外还有其他用于度量相似度的函数，这些函数统称为核函数（Kernel Function）。

核函数的意义

将高斯核函数利用欧氏距离公式展开：
\[\begin{aligned} k(x,l^{(i)})&=e^{-\frac{||x-l^{(i)}||^2}{2σ^2}}\\ &=e^{-\frac{∑_{j=1}^n(x_j-l^{(i)}_j)^2}{2σ^2}} \end{aligned}\] 对于某个特定的\(i\):
如果\(x≈l^{(i)}\)（两者的欧氏距离非常近）,\(f_i≈e^{-\frac{0}{2σ}}≈1\)。
如果\(x\)和\(l^{(i)}\)的欧氏距离非常远,\(f_i≈e^{-\frac{∞}{2σ}}≈0\)。
对于任何一个样本\(x\),都可以计算\(f_1\),\(f_2\),\(f_3\)三个特征。 在图像上反映相似度与两者距离之间的关系即为高维空间中的高斯分布，且σ越大，图像梯度越小。

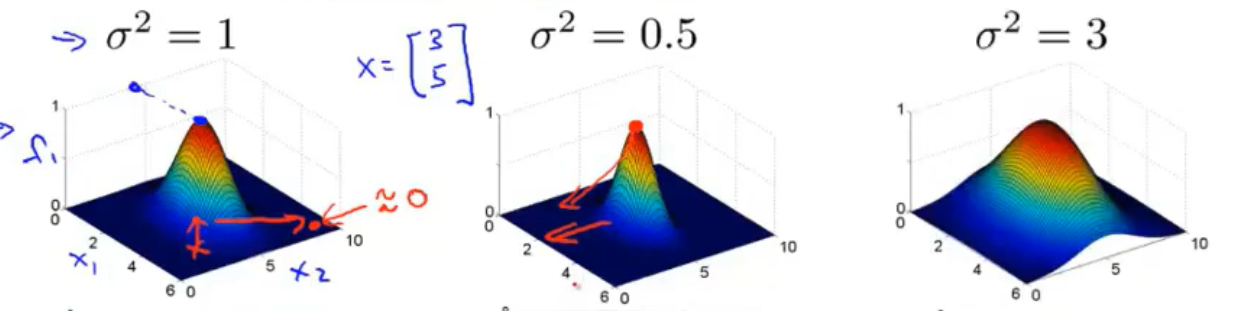
△当\(l^{(1)}=[3,5]^T\)时x的坐标\([x_1,x_2]^T\)与相似度的关系。

决策边界

再回到之前样本在特征上的分布：

如果样本距离某个\(l^{(i)}\)非常近（洋红色），那么边界函数输出的结果大于0，预测\(y=1\)。
如果样本距离三个\(l^{(i)}\)非常远（蓝色），那么边界函数输出的结果小于0，预测\(y=0\)。
当样本足够多的时候，所有\(y=1\)的点的边界即为决策边界，此时的决策边界是非线性的。