《机器学习》 周志华 1-5章笔记

作者为博主的同事 黄欣迪

第一章 绪论

• 1.1 引言

  什么是机器学习？ 机器学习是致力于研究如何通过计算的手段，利用经验来改善系统自身的性能
  经验——数据 模型——算法 通过相应的算法分析数据——得出结论
  一些文献用“模型”指全局性结果（决策树） 用“模式”指局部性结果（一条规则）

• 1.2 基本术语

  进行机器学习的前提是要有数据，例如给细胞的数据，并对给定细胞的大小，形态等进行记录
  这组记录的集合称为一个“数据集”，其中每一条记录是关于一个事件或对象的描述，称为一个“示例”或“样本”
  对于细胞的描述，如大小、形状，称为“属性”或“特征”
  属性上的取值例如圆形、椭圆形，称为“属性值” 属性张成的空间称为“属性空间”、“样本空间”或“输入空间”
  例如大小、形状、颜色张成的三维空间对于每一个样本都能找到对应的坐标向量，称为“特征向量” 从数据中学得模型的过程称为“学习”或“训练” 对于潜在规律自身，称为“真相”或“真实” 本书有时将模型称为“学习器” 拥有了标记信息的示例，称为“样例”
  如果预测的是离散值，称为“分类” 若为二分类，则是正类和反类 预测的是连续值，称为“回归”
  监督学习和无监督学习 前者是分类和回归是前者的代表 聚类是后者的代表
  泛化模型是我们所想要找到的，强泛化模型可以更好适用于整个样本空间

• 1.3 假设空间

  泛化学习：通过对训练集中瓜的学习已获得对没有见过的瓜进行判断的能力
  假设空间：对所有假设组成的空间进行搜索，搜索目标是找到与训练集fit的假设

• 1.4 归纳偏好

  偏好：对于不同的模型，它的偏好是不一样的，例如有一个模型更偏好某一特征，它会根据将该特征进行结果的认定
  任何一个有效的机器学习模型必有其归纳偏好，否则会被假设空间中看似在训练集中“等效”的假设所迷惑
  算法A优于算法B P9 具体论证 算法A和算法B的期望相同 与算法无关

• 1.5 发展历程
  

• 1.6 应用现状

• 1.7 阅读材料
  ## 第二章 模型评估与选择

• 2.1 经验误差与过拟合

  分类错误的样本占样本总数的比例称为“错误率”
  m个样本中a个错误
  \[E=\frac{a}{m}\]
  相对的精度=1-错误率
  过拟合的定义为学习器将训练集的自身特点当作了所有潜在样本的性质，这样会导致泛化性下降
  难以在机器学习的过程中避免过拟合

• 2.2 评估方法

  测试集尽量不要出现在训练集当中

• 2.2.1 留出法

  将数据集D划分为两个互斥的集合 一个为训练集S 另一个为测试集T
  划分尽量保持数据分布的一致性 分层采样
  一般而言测试集至少含30个样例
  \(\frac{2}{3}\)到\(\frac{4}{5}\)的样本用于训练 其余样本用于测试

• 2.2.2 交叉验证法

  数据集D划分为k个大小相似的互斥子集 每个子集都尽可能保持数据分布的一致性 P26 D——D1 D2 D3…. D10 D1 D2….D9 训练集 D10 测试集 D1 D2….D8 D10 训练集 D9 测试集 10次10折交叉验证
  留一法：交叉验证法的特例——只留下一个样本作为测试集

• 2.2.3 自助法

  给定包含m个样本的数据集D 对它进行采样产生数据集D’ 每次随机从D中挑选一个样本 将其拷贝到D’中 重复执行m次
  得到了包含m个样本的数据集D’ m次采样中始终不被采集到的概率是 \[ (1-\frac{1}{m})^m \]
  极限值约为0.368 即D中约有36.8%的样本没有在D’中出现
  用D/D’作为测试集（/表示集合减法) 这样的测试结果叫做“包外估计”
  自助法适用于数据量较小的数据集 留出法和交叉验证法适用于数据量足够的数据集

• 2.2.4 调参与最终模型

  调参往往需要设定一个步长 在对应步长内取值 因为无法在实数范围内取完所有值
  测试数据：模型在实际使用中遇到的数据

• 2.3 性能度量

  定义：衡量模型泛化能力的评价标准
  性能度量反映了任务需求——不同的性能度量导致不同的评判结果——模型的好坏是相对的
  回归任务最常用的性能度量是“均方误差” \[E(f;D)=\frac{1}{m}\sum_{m=1}^{m}(f(x_i)-y_i)^2\]
  对于数据分布D和概率密度p(’) 均方误差为
  \[E(f;D)=\int_{x\sim D} (f(x)-y)^2p(x)dx\]
  以下主要是分类任务中常用的性能度量

• 2.3.1 错误率与精度

  错误率和精度是分类任务中最常用的两种性能度量 既可以适用于二分类任务 也能适用于多分类任务
  对样例集D 分类错误率定义为
  \[E(f;D)=\frac{1}{m}\sum_{i=1}^{m}\prod_{}(f(x_i)\neq{y_i})^2\]
  精度定义为
  \[acc(f;D)=\frac{1}{m}\sum_{i=1}^{m}\prod_{}(f(x_i)\neq{y_i})^2=1-E(f;D)\]

• 2.3.2 查准率、查全率与F1

  实例：在信息检索中，经常关心的是“检索出的信息中有多少比例是用户感兴趣的”“用户感兴趣的信息中有多少被检索了出来”
  “查准率”(precision)和“查全率”(recall)是更为适用于此类需求的性能变量
  对于二分类问题 可将样例根据真实类别与学习器预测类别的组合划分为四种情形
  真正例 假正例 真反例 假反例 令其为 TP、FP、TN、FN TP+FP+TN+FN=样例总数
  查准率P与查全率R分别定义为
  \[P=\frac{TP}{TP+FP}\]
  \[R=\frac{TP}{TP+FN}\]
  查全率和查准率除了在一些简单任务中都比较高以外 一般一个高另一个低
  画出模型实时的P-R图可以判断该模型的性能 如果P-R曲线被另一个模型包裹 那么可以认为被包裹的模型性能差
  最终可以根据比较P-R曲线围成面积的大小来确定模型性能的好坏(该值不容易估算)
  平衡点(Break-Event Point, 简称BEP)：查准率=查全率时的取值(平衡点大 学习性能优)
  但更常用的是F1度量
  \[F1=\frac{2*P*R}{P+R}=\frac{2*TP}{样例总数+TP-TN}\]
  如果在实际问题中对查准率和查全率的偏重不同的话 引入Fβ
  \[\frac{1}{F1}=\frac{1}{2}(\frac{1}{P}+\frac{1}{R})\]
  \[\frac{1}{F_\beta}=\frac{1}{1+\beta^2}(\frac{1}{P}+\frac{\beta^2}{R})（\beta>1 查全率影响大）（\beta<1 查准率影响大）\] 以上公式可以看出F1是基于查准率和查全率的调和平均定义的
  Fβ则是基于加权调和平均定义的 与算术平均和集合平均相比 调和平均更重视较小值
  考虑实际情况中需要在n个二分类混淆矩阵上综合考察查全率和查准率
  做法一：在各个混淆矩阵中分别计算P和R 计算平均值 代入F1
  做法二：计算TP、FP、TN、FN的平均值 代入P和R 再代入F1

• 2.3.3 ROC与AUC

  学习器一般是为测试样本产生一个实值或概率预测 使用该预测值与分类阈值进行比较 若大于阈值则为正类 反之为反类
  预测结果的好坏决定了学习器的泛化能力
  该分类过程相当于在排序中以某个截断点将样本分为两个部分 前一部分判做正例 后一部分判做反例
  ROC曲线则是以排序本身的好坏来判定学习器泛化性能的
  ROC曲线全称是“受试者工作特征”(Receiver Operating Characteristic)
  ROC曲线的定义
  纵轴：“真正例率”
  \[TPR=\frac{TP}{TP+FN}\]
  横轴：“假正例率”
  \[FPR=\frac{FP}{TN+FP}\]
  真正问题中对于有限个测试样例
  设给定m+个正例 m-个反例进行排序
  首先将分类阈值设为最大——所有样例均预测为反例 初始的真正例率和假正例率均为0 初始坐标(0,0)
  现在预测一个样本 如果为真正例 标记点的坐标为
  \[(x,y+\frac{1}{m^+})\]
  如果为假正例 标记点的坐标为
  \[(x+\frac{1}{m^-},y)\]
  进行学习器比较时 若一个学习器的ROC曲线被另一个学习器的曲线完全包住 则可断言后者的性能优于前者 若两个学习器的ROC曲线发生交叉 则不能断言
  同样 如果要比较两个学习器 较为合理的判据是比较ROC曲线下的面积 即AUC
  AUC可以估算为
  \[AUC=\frac{1}{2}\sum_{i=1}^{m-1}(x_{i+1}-x_i)*(y_i+y_{i+1})\] 但在实际问题中如何考虑排序的误差
  \[l_{rank}=\frac{1}{m^+m^-}\sum_{x^+\in{D^+}}\sum_{x^+\in{D^+}}(\prod_{}(f(x^+)<f(x^-))+\frac{1}{2}\prod_{}(f(x^+)=f(x^-)))\] \[AUC=1-l_{rank}\] 理解：如果正例的预测值小于反例 则记一个罚分 如果正例的预测值等于反例 则记0.5个罚分

• 2.3.4 代价敏感错误率与代价曲线

  实际问题中 对于不同类型的错误所造成的后果不同
  例如在医疗诊断中，错误地把患者诊断为健康人与错误地把健康人诊断为患者的结果不同
  对于这类问题可以将预测错误的cost设为cost1和cost2
  代入之前的公式可以计算出总体代价最小时的错误率
  在非均等代价下 ROC曲线不能直接反映出学习器的期望总体代价 这时需要使用代价曲线
  具体可见P36

• 2.4 比较检验（以下为各种概率论中的假设检验）

• 2.5 偏差和方差

  泛化误差可以分解为偏差、方差与噪声之和 P45

第三章 线性模型

• 3.1 基本形式

  给定由d个属性描述的示例
  \[x=(x_1;x_2...;x_d)\]
  其中xi是x在第i个属性上的取值
  线性模型学习的是通过属性的线性组合来进行预测的函数 即
  \[f(x)=w_1x_1+w_2x_2+w_3x_3+.....+w_dx_d+b\]
  一般用向量写成
  \[f(x)=w^Tx+b\]
  w和b学得后 模型就得以确定

• 3.2 线性回归

  给定数据集
  \[D={(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}\]
  其中
  \[x_i=(x_{i1};x_{i2};...;x_{id}), y_i\in{R}\]
  线性回归试图学得一个线性模型以尽可能准确的预测实值输出标记
  首先可以将离散型属性通过连续化将其转化为连续值
  例如二值属性“身高” 高=1 矮=0
  线性回归试图学得
  \[f(x_i)=wx_i+b, 使得f(x_i)\approx{y_i}\]
  均方误差是回归任务中最常用的性能度量 所以试图让均方误差最小化
  具体推导过程 P54
  一个属性只有一个权重 d个属性就会有d个权重
  可以考虑广义的情况 比如lny

• 3.3 对数几率回归

  对数几率函数
  \[y=\frac{1}{1+e^{-z}}\]
  也就称为sigmoid函数
  预测值z 通过z来找y y是逼近0或者1 由此判断预测为正或反

• 3.4 线性判别分析

  线性判别分析(Linear Discriminant Analysis LDA)是一种经典的线性学习方法，主要用于二分类问题
  目标 同类别的方差最小 不同类别的方差最大
  (该方法应用比较少)

• 3.5 多分类学习

• 3.6 类别不平衡问题

  过采样：不能重复采样 会造成过拟合
  欠采样：去除一些样本 让正反例数量接近 然后再进行学习

• 3.7梯度下降法(补充)

第四章 决策树

• 4.1 基本流程

  决策树的生成是一个递归过程 学习目的是为了产生一棵泛化能力强 即处理未见示例能力强的决策树

• 4.2 划分选择

  最关键的是如何选择最优化分属性 希望随着划分过程的进行 决策树的分支结点所包含的样本尽可能属于同一类别
  即结点的“纯度”越来越高

• 4.2.1 信息增益

  “信息熵”(information entropy)是度量样本集合纯度最常用的一种指标
  假定当前样本集合D中第K类样本所占比例为\(P_k(k=1,2,...,|y|)\)，则D的信息熵定义为
  \[Ent(D)=-\sum_{K=1}^{|y|}p_klog_2P_k\]
  Ent(D)的值越小 D的纯度越高
  什么是熵：对一种事物的不确定性就叫熵 比如买西瓜 不知道买哪一个是好瓜 这就是熵
  信息：消除这种不确定性的事物（调整概率、排除干扰、确定情况）
  噪音：不能消除某人对某件事情不确定性的事物
  数据：信息+噪音
  假设一件事情有八种等可能的结果 相当于抛三枚硬币 熵为3bit
  若每种情况概率分布不相等(一般分布)
  \[A=\frac{1}{2}|B=\frac{1}{3}|C=\frac{1}{6}\]
  \[P(A)=\frac{1}{2}(log_26-log_23)\]
  \[P(B)=\frac{1}{3}(log_26-log_22)\]
  \[P(C)=\frac{1}{6}(log_26-log_21)\]
  \[Ent(D)=P(A)+P(B)+P(C)\]
  得知信息的前后 不确定性的变化——熵的差额 就是信息的量
  例如ABCD四道选择题 等可能的话熵为2bit
  如果知道C有一半可能是正确的 那么
  \[P(A)=P(B)=P(D)=\frac{1}{6}|P(C)=\frac{1}{2}\]
  现在的熵为
  \[\frac{1}{6}log_26+\frac{1}{6}log_26+\frac{1}{2}log_22+\frac{1}{6}log_26=1.79\]
  所以 知道C有一半可能正确的条件后 现在的不确定性是1.79 那么信息量就是0.21
  西瓜数据集2.0 P76
  17个样例 8个好瓜 9个坏瓜 一般分布
  先算出信息熵 根节点
  \[Ent(D)=\frac{8}{17}log_2\frac{17}{8}+\frac{9}{17}log_2\frac{17}{9}=0.998\]
  然后计算每一个特征不同的信息增益
  三种色泽 先算每一种的Ent 然后分权 相加 与根结点的熵作差 得到有关色泽的信息增益
  \[Ent(D_1)=\frac{3}{6}log_2\frac{6}{3}+\frac{3}{6}log_2\frac{6}{3}=1.000\]
  \[Ent(D_2)=\frac{4}{6}log_2\frac{6}{4}+\frac{2}{6}log_2\frac{6}{2}=0.918\] \[Ent(D_3)=\frac{1}{5}log_2\frac{5}{1}+\frac{4}{5}log_2\frac{5}{4}=0.722\]
  \[Gain(D,色泽)=Ent(D)-\sum_{v=1}^3\frac{|D^v|}{D}Ent(D^v)=0.998-(\frac{6}{17}*1.000+\frac{6}{17}*0.918+\frac{5}{17}*0.722)=0.109\] 根据计算的结果信息增益越高 作为第一轮选择
  以此类推

• 4.2.2 增益率(C4.5算法)

  信息增益准则对可取值数目较多的属性有所偏好
  所以C4.5决策树算法 是先计算Gain 也就是分权后相加的熵 再用该改值除以IV(a)
  \[Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}=\frac{0.109}{\frac{6}{17}log_2\frac{17}{6}+\frac{6}{17}log_2\frac{17}{6}+\frac{5}{17}log_2{17}{5}}\]
  使用增益率方法时 先选出信息增益前五位的信息 随后利用该方法进行进一步筛选

• 4.2.3 基尼指数(CART算法)

  Classification and Regression 该方法既可以进行分类也可以进行回归
  例子：首先先进行统计 西瓜2.0数据集
  第一个特征色泽 分别统计在青绿这一信息中 是好瓜的个数和不是好瓜的个数
  乌黑中 是好瓜的个数和不是好瓜的个数 以此类推
  如果统计中有缺失值例如？？？ 直接跳过
  CART都是二叉树的模型 衡量纯度的方法
  Gini index 抽两次 抽得样本中不同的概率来衡量纯度
  例如B站 P59
  \[Gini index=1-(\frac{105}{105+39})^2-(\frac{39}{105+39})^2\]
  基尼指数越大 表示这两个大概率是不同的 所以纯度就下降
  希望基尼指数越大越好
  补充：基尼指数的计算代码
  

  def gini_index_single(a,b):  
      single_gini=1-((a/(a+b))**2)-((b/(a+b))**2)  
      return round(single_gini,2)  
  def gini_index(a,b,c,d):  
      zuo = gini_index_single(a,b)  
      you = gini_index_single(c,d)  
      gini_index = zuo*((a+b)/(a+b+c+d))
                     +you*((c+d)/(a+b+c+d))  
      return round (gini_index,2)  

  补充回归问题
  SKlearn 计算每一个阈值所对应均方值的最小值

• 4.3 剪枝处理

• 4.3.1 预剪枝

  目的是防止过拟合
  首先将之前的西瓜数据集2.0分为5/5的训练集以及3/4的测试集
  根据5/5的训练集先生成一颗决策树 采用的是信息增益准则
  引入验证集之后 对于一个结点 先计算不划分该结点时的准确率
  对于这个例子 5/5的训练集我们认为第一个结点脐部全为好瓜 对于测试集 准确率为42.9%
  划分后 我们获得的标记和测试集进行比较 准确率为71.4%
  所以我们决定对脐部进行划分 之后的特征也由此类推
  这样的方法确实可以防止过拟合的产生 但也带来了欠拟合的风险

• 4.3.2 后剪枝

  后剪枝主要是在生成决策树之后 自下而上的进行判断
  这样的方法能够有效的防范欠拟合的的风险
  但因为是在生成决策树之后进行 所以训练时间的开销会比未剪枝和预剪枝要大得多

• 4.4 连续与缺失值

  连续值处理
  C4.5算法采用二分法 例子：西瓜数据集3.0
  对于该方法主要计算两个取值 1、信息增益 2、划分点
  对于每一个划分点进行计算 找到信息增益最大的点 以及最大的信息增益即可
  缺失值处理
  对于有缺失值的数据来说 计算信息增益时我们只需要计算该特征下无缺失值所获得的信息增益 再用它来乘以无缺失值数据所占比例即可
  例如有在色泽特征下 有14个无缺失值的数据 一共有17个数据
  \[Gain=\frac{14}{17}*Gain(14)\]
  其他方法
  离散值
  1、众数填充 2、相关性最高的列填充
  连续值
  1、中位数 2、相关性最高的列做线性回归进行估计

• 4.5 多变量决策树

  单变量决策树生成的函数图像的分割线总是与函数轴垂直或平行
  多变量决策树生成的函数图像的分割线相对复杂 一般是曲线
  多变量的分界点主要是对于特征的线性组合进行分割

第五章 神经网络

• 5.1 神经元模型

  这本书主要讲的是神经网络和机器学习两个学科领域的交叉部分
  M-P神经元模型 神经元接收到来自n个其他神经元传递过来的输入信号 这些输入信号通过带权重的链接进行传递
  神经元接收到的总输入值将与神经元的阈值进行比较 然后通过激活函数处理以产生神经元的输出
  常用sigmoid函数作为激活函数 把这样的多个神经元进行链接 就得到了神经网络

• 5.2 感知机与多层网络

  感知机(perceptron)由两层神经元组成 输入层接收外界输入信号后传递给输出层 输出层是M-P神经元 亦称“阈值逻辑单元”
  感知机能容易地实现逻辑与、或、非运算 假设
  \[y=f(\sum_iw_ix_i-\theta)\]
  激活函数为阶跃函数 可以很容易地实现三种运算
  例：与运算 令\(w_1=w_2=1\), \(\theta\)=2 仅当\(x_1=x_2=1\)时候 y=1
  一般情况下 给定训练数据集 权重wi以及阈值theta可以通过学习得到
  我们也可以设定阈值\(\theta\) 为一个固定的输入-1,0的“哑结点”(dummy node)所对应的连接权重\(w_n+1\)
  那么就只用对权重进行学习 对于权重的调整 对训练样例(x,y) 若当前的感知机的输出为y’那么权重调整为
  \[w_i\gets{w_i}+\Delta{w_i}\]
  \[\Delta{w_i}=\eta(y-y')x_i\]
  其中\(\eta\)为学习率 是一个0-1之间的数 从调整方程可以看出 若感知机对于样本的预测是正确的 那么w不发生变化
  反之进行权重调整
  感知机的学习能力非常有限 因为它只拥有一层功能神经元 因为上述问题都是线性可分的(linearly separable) 所以存在一个线性超平面能将它们分开 这样感知机的学习过程一定会收敛(converge) 以求得适当的权向量w
  反之 若问题不是线性可分的 感知器的权重将无法收敛 发生震荡 这时就需要多层神经元来解决问题
  若引入两层的感知机 则可以解决亦或问题
  输出层与输入层之间的一层神经元被称为隐层或隐含层(hidden layer) 隐含层和输出层神经元都是拥有激活函数的功能神经元
  对于“多层前馈神经网络”来说 每层神经元与下一层神经元全互连 神经元之间不存在同层连接 也不存在跨层连接
  输入层：仅接收输入，不进行函数处理
  隐层和输出层包含功能神经元 单隐层指只含有一层隐层的网络 单隐层网络也被称为两层网络
  神经网络的学习过程 就是根据训练数据来调整神经元之间的“连接权”(connection weight)以及每个功能神经元的阈值

• 5.3 误差逆传播算法(反向传播算法)

  误差逆传播(BackPropagation, 简称BP)算法就是其中的代表 BP算法不仅可用于多层前馈神经网络 还可以用于其他神经网络
  BP算法是什么样的
  给定训练集
  \[D={(x_1,y_1),(x_2,y_2),...,(x_m,y_m)}, x_i\in{R^d},y_i\in{R^d}\]
  即输入示例有d个属性描述 输出l维实质向量(如图所示)
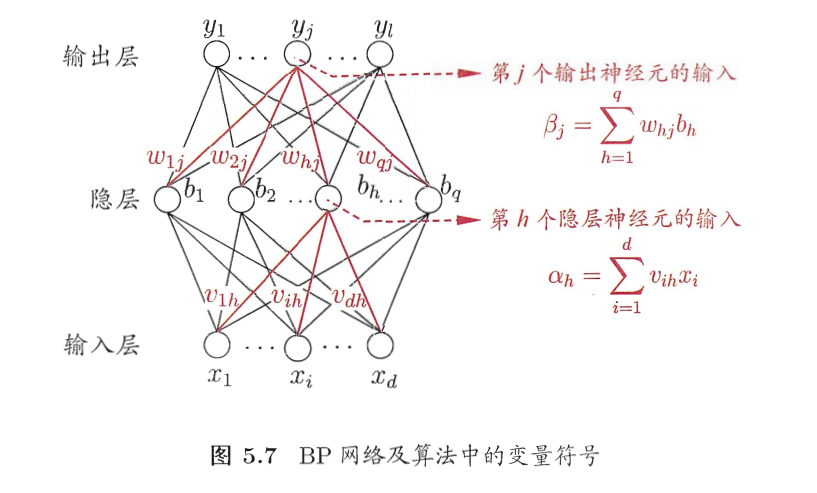  假设隐层和输出层神经元都是用sigmoid函数
  对于训练例\((x_k,y_k)\) 假定神经网络的输出为\(y'_k=(y'_{1k},y'_{2k},...,y'_{lk})\) 即
  \[y'_{jk}=f(\beta_j-\theta_j)\]
  则网络在\((x_k,y_k)\)上的均方误差为
  \[E_k=\frac{1}{2}\sum_{j=1}^l(y'_{jk}-y_{jk})^2\]
  图中的网络有(d+l+1)q+l个参数需确定：输入层到隐层的dq个权值、隐层到输出层的ql个权值、q个隐层神经元的阈值、l个输出层神经元的阈值
  BP是一个迭代学习算法 对于参数进行更新的规则与之前类似 任意参数v的更新估计式为
  \[v\gets{v}+\Delta{v}\]
  推导隐层到输出层的连接权\(w_{hj}\)