9.3. K均值算法的优化

K均值算法的优化

多次随机初始化

初始化的状态不同，可能最后得到的结果是不一样的。
随机初始化聚类中心的其中一种方法为：
随机选择K个样本\(μ_1...μ_k\)作为\(K\)个聚类中心。
但是按如上的随机初始化方式可能导致最后的分类的结果不同，并且有可能使得代价函数\(J\)落入局部最优解而不是最小值。

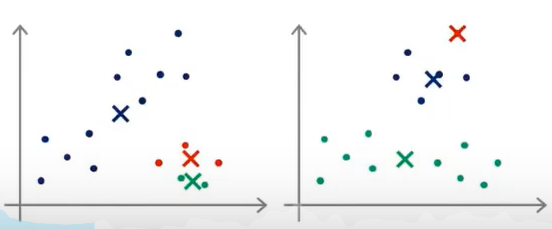
解决这个问题的方法是多次（比如50-100次）随机初始化聚类中心并运行K-Means算法，每运行一次都会得到代价函数的值 \(J\)，最后从这些代价函数的值中挑选最小的一个。
实验说明，当\(K\)的取值比较小（2-10）时，多次随机初始化能够有效改善出现局部最优解的情况，而\(K\)的取值很大时，这种方法不会起到比较好的改善。

正确选取\(K\)的数量

肘部法则

通常在数据集中有多少个类是不清楚的，因此用一个自动化的算法内选择聚类的数量是困难的。但是仍然有一些法则能够帮助设置聚类数量，其中一个法则称为肘部法则（Elbow method），具体方法如下：
通过不断改变K的值运行K-Means算法，计算出不同的代价函数值\(J\)，如图所示：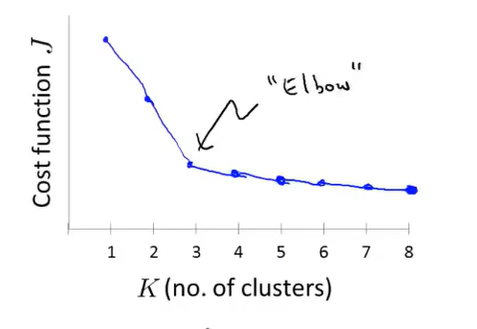
图示的拐点常常被用于设置聚类数据。
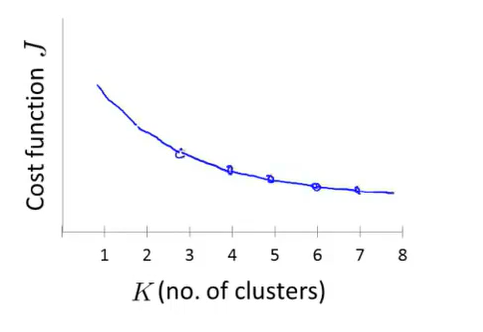
但是在实际中，往往曲线的拐点并不明确，比如如下所示，因此通过肘部法则来选取聚类数量的方法具有局限性。

根据后续目的选择\(K\)

很多时候运行K-Means算法是为了一些后续的目的，比如市场划分等等。如果后续的目的能够给出一个评估标准，那么决定聚类数量的最好方法是看那个聚类数量更适合这个评估标准。
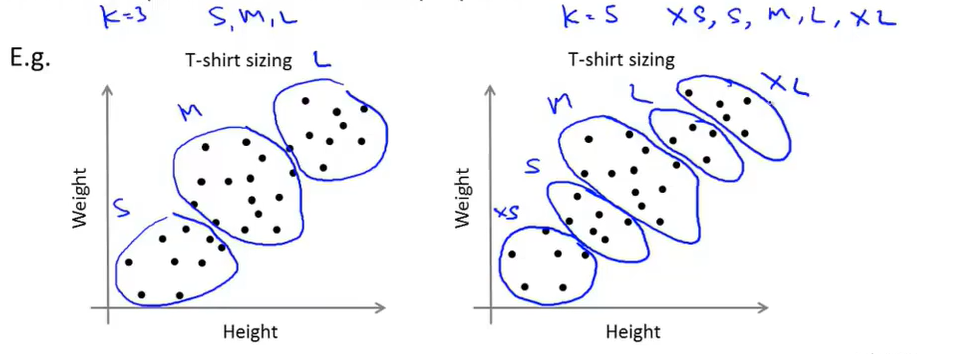
比如要分出衣服的尺寸，可以根据衣服的尺寸：S，M，L，将K设置为3；或者根据XS,S,M,L,XL将K设置为5，如下图所示。