10.2. 算法思路和流程

主成分分析算法的思路和流程

主成分分析,PCA,是最流行的降维方法之一。

主成分分析问题

PCA会找一个低维平面，将所有的数据投影到这个平面内，并使得的所有数据点到这个地维平面的距离（称为投影误差）之和最短。
在应用PCA之前，通常会将数据归一化和特征缩放，使得所有的数据在可比的范围之内。
具体而言，PCA会在\(n\)维的数据空间中寻找到\(K\)个能够代表这个低维平面的方向向量\(u^{(1)},...,u^{(K)}\)，使得这\(K\)个向量所定义的低维平面，即线性代数中这些向量的张成空间\(Span[u^{(1)},...,u^{(K)}]\)。
根据线性代数的相关知识，这\(K\)个向量应当是线性不相关且两两正交的。

PCA与线性回归的区别

需要注意的是，尽管看上去比较相似，但是PCA并不是线性回归。在线性拟合中需要寻找的是数据点到直线的垂直距离，而在PCA需要找到的是数据点到直线的最短距离，如图所示。

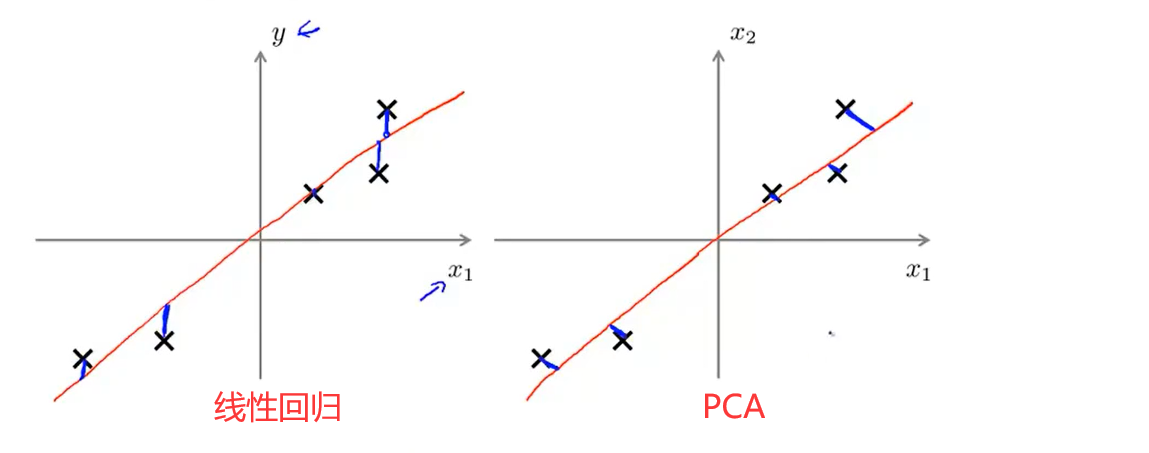
而且线性回归的目的是寻找给定某个\(x\)的预测值\(y\)，而PCA只是单纯的在\(x_1,..x_n\)的\(n\)维特征空间中寻找一个低维平面。但是PCA和线性拟合运用的思想是相似的。

主成分分析流程

新加坡国立大学讲义中关于PCA的部分：NUS-Machine Learning:5.特征-PCA

对于训练集：\(x^{(1)},..,x^{(m)} ∈ \mathbb{R}^n\)，首先对其进行归一化处理或者是特征缩放，使得所有的特征都具有可比性。
然后计算训练集的协方差矩阵\(\Sigma\)：
\[Σ=\frac{1}{m}∑_{i=1}^{n}(x^{(i)})(x^{(i)})^T\]
Σ是一个\(n × n\)的矩阵。
对协方差矩阵应用奇异值分解，得到协方差矩阵的所有特征向量所组成的矩阵\(U\)。
\[U=[u^{(1)}|u^{(2)}…|u^{(k)}…|u^{(n)}]\] \(U\)是一个\(n × n\)的矩阵。
现在将这些特征向量按照分别所对应的特征值从大到小的顺序排列，选择其中\(k\)的最大的特征向量构成主成分矩阵\(U_{reduce}\)。
新的降维后的数据集\(z^{(1)},..,z^{(m)}∈ \mathbb{R}^k\)可以通过投影（即乘上转置矩阵）：
\[z^{(i)}=U_{reduce}^Tx^{(i)}\] 这样每一个\(z\)都是一个\(k\)维的向量。