11.3. 异常检测算法的评价·关键变量

异常检测算法的评价·关键变量

异常检测算法的实数评价

实数评价

评估学习算法的重要方法是实数评价，即对评价的指标返回一个实数，通过实数的大小来直观表示学习算法在这一指标上的优劣性。
假设有一系列带标签（标记正常或者异常）的数据集用于异常检测算法，从数据集中分离出一个无标签的训练集（其中绝大部分的数据都应该是正常/异常的），使用训练集来建立数据集的概率密度模型\(p(x)\)。
接着建立有标签的交叉验证集和测试集来评估这个算法。
> 在实际训练中，数据集中正常样本的数量应该比异常样本数量要多得多。推荐的数据划分比例：训练集：测试集：交叉验证集=60:20:20

将测试集和验证集的数据放入模型\(p(x)\)，模型给出预测的结果。
由于该数据集是一个偏斜类数据集，因此单纯的使用算法准确率指标对其评估并不是一个好的选择。在偏斜类问题中，常采用的指标有：
- 真阳性/真阴性/假阳性/假阴性率 - 查准率和召回率 - F值

偏斜类问题/查准率、召回率/F值的知识见：7.2. 查准率和召回率

关键变量的选取

阈值（\(ɛ\)）的选取

阈值\(ɛ\)很大程度上会影响算法的性能：
\[y=\begin{cases} 1,p(x_{test})<ɛ \\ 0,p(x_{test})≥ɛ \end{cases}\] 通常设定一系列的\(ɛ\)值，取能够使得F值最大的\(ɛ\)作为最终阈值。也可以使用交叉验证集来选择\(ɛ\)。

特征的选取

特征变换

由于异常检测的关键在于利用高斯分布的概率密度函数进行计算，因此在将数据输入进算法前有必要绘制数据在某些特征上的分布以检验是否符合高斯分布的特性。
虽然数据不符合高斯分布，算法也能够正常运行，但是算法性能会有所损失。常见的做法是使用一些变换将这类数据变为类似于高斯分布的形式，比如下图对数据进行的对数变换。

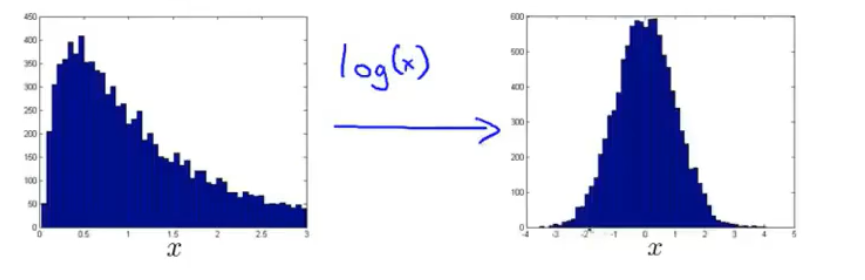
常用的特征变换：
- 对数变换：\(x→log(x+c)\)
- 分数幂指数变换：\(x→x^{\frac{1}{c}}\)

寻找特征

基本思路是用误差分析：观察测试集和验证集中识别错误的数据，再想出另外的特征加入到原来的算法中。
如果异常的样本和正常的样本给出的\(p(x)\)值差异不大，则应当观察数据在其他新特征上的分布规律，这些新特征应该能够明显的区分异常样本和正常样本。
通常可以通过将一些线性相关的特征进行非线性组合，来打破线性相关性。从而获得一些新的更好的特征（异常数据的该特征值异常地大或小从而能够更明显地被区分开）。
例如，在检测数据中心的计算机状况的例子中，一般情况下网络通信量\(x_1\)越高，CPU负载\(x_2\)越高，这样的两个特征有可能不容易区分异常的服务器（网络通信量正常，但CPU负载高）。此时可以用CPU负载与网络通信量的比: \[\frac{x_2}{x_1}\] 作为一个新的特征，以放大CPU负载在网络通信量正常时的效果。新的特征能够很好的凸显上述问题：如果该值异常地大，有可能意味着该服务器是陷入了一些问题中。