11.5. 多元异常检测算法

多元异常检测算法

问题动机

实际问题中的有些异常并不能直接通过一个变量指标观测出来，这时候就需要引入多个变量综合进行分析，比如如下的这个例子。
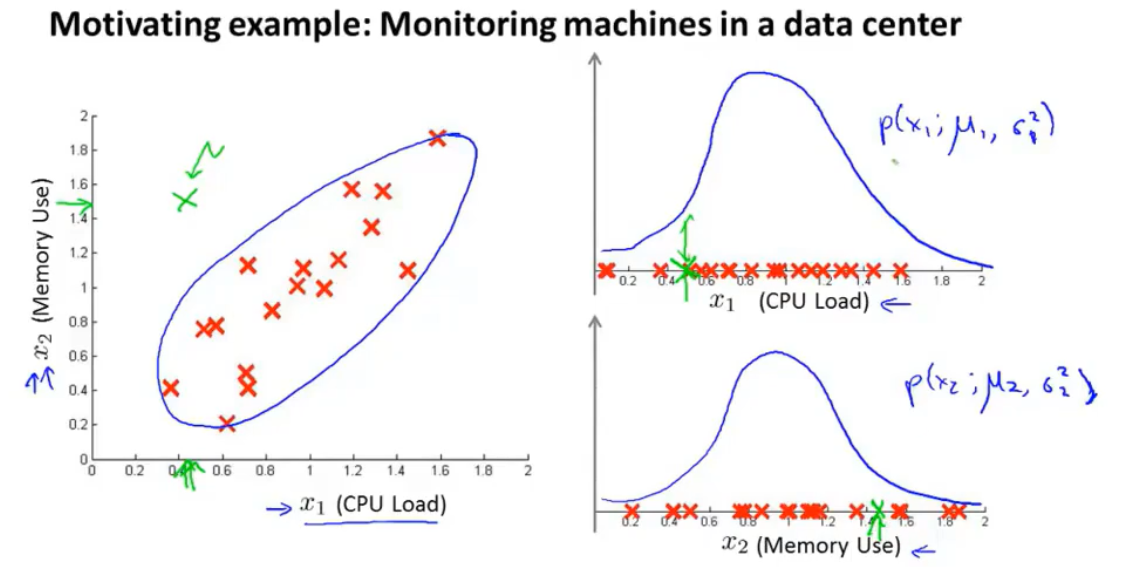
如图所示，在计算机状态监测中，考虑CPU负载和内存使用两个变量，正常数据在这两个变量上的分布记为红色标记，现在引入一个绿色的异常数据：如果观察绿色的异常数据在分别的两个变量指标上的分布（图右部分），发现这个异常数据很难在整个数据集中被发现，而通过综合两个变量指标，观察二维分布，则比较容易发现这个异常的数据。

多元高斯分布

为了进一步改进异常检测算法，需要用到多元高斯分布的相关知识。
假设特征变量\(x∈R^n\)，现在不通过为每一个特征分别建模\(p(x_i)\)的方法，转而对整体直接建立模型\(p(x)\)。
根据多元高斯分布的公式：
\[p(x;μ,Σ)=\frac{1}{(2π)^{\frac{n}{2}}|Σ|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-μ)^TΣ^{-1}(x-μ))\] 其中\(Σ∈R^{n×n}\)，是\(x\)的协方差矩阵。\(|Σ|\)表示\(Σ\)的行列式。
\(μ∈R^n\)是一个均值向量。
\(p(x)\)在高维空间中呈现出高斯分布。
类比与二维高斯分布，\(Σ\)内的元素值控制极值点的大小，同时控制从极值点到零点各方向的变化率（同时非对角线上的元素控制着各维度之间的相关性）。\(μ\)控制极值点的位置。

多元高斯分布的参数估计问题

假设随机变量\(x∈R^n\)的\(m\)个样本\(\{x^{(1)},x^{(2)},...,x^{(m)}\}\)，可以利用如下的公式对\(μ\)和\(Σ\)进行参数估计:
\[μ=\frac{1}{m}∑_{i=1}^mx^{(i)}\] \[Σ=\frac{1}{m}∑_{i=1}^m(x^{(i)}-μ)(x^{(i)}-μ)^T\]

使用多元高斯分布的多元异常检测算法

假设数据集有\(m\)个样本\(\{x^{(1)},x^{(2)},...,x^{(m)}\}\)，首先假设数据集的分布服从多元高斯分布，算法流程如下：
1. 使用样本数据建立\(p(x)\)的模型：
\[μ=\frac{1}{m}∑_{i=1}^mx^{(i)}\] \[Σ=\frac{1}{m}∑_{i=1}^m(x^{(i)}-μ)(x^{(i)}-μ)^T\] 2. 建立\(p(x)\)的模型：
\[p(x;μ,Σ)=\frac{1}{(2π)^{\frac{n}{2}}|Σ|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-μ)^TΣ^{-1}(x-μ))\] 3. 对于给定的新样本\(x_{new}\)，带入\(p(x)\)的模型中进行计算得到\(p(x_{new})\) 4. 设定阈值\(ɛ\),如果\(p(x_{new})<ɛ\)则表明\(x_{new}\)为异常数据。

多元异常检测算法与原始异常检测算法的关系

原始模型：
\[p(x)=Π_{i=1}^np(x_i,μ_i,σ^2_i)\]
多元高斯模型：
\[p(x;μ,Σ)=\frac{1}{(2π)^{\frac{n}{2}}|Σ|^{\frac{1}{2}}}exp(-\frac{1}{2}(x-μ)^TΣ^{-1}(x-μ))\] 其实原始模型是多元高斯模型的一种特殊情况：所有的特征之间都独立不相关，而多元高斯分布模型考虑到了特征之间的相关性。
特征不相关时，协方差矩阵\(Σ\)是一个对角矩阵：
\[Σ=\begin{bmatrix} σ^2_1 & ... &...\\ ... & σ^2_2 & ... \\ ... & ... & ... \\ ... & ... & σ^2_n \\ \end{bmatrix}\] 带入多元高斯模型中即可推导出原始模型。

模型对比

	原始模型	多元高斯模型
探测关联特征的方式	手动创建一个新特征	自动捕捉特征之间的关系
计算性能	计算成本低，能够适应数量巨大的特征	由于需要计算协方差矩阵，计算成本高，仅能对特征数少的情况适用
数据要求	可以适用于数据少，特征多（\(m<n\)）的情况	由于协方差矩阵必须可逆，因此要求\(m>n\)甚至是\(m>>n\)

手动创建特征的方式见9.9. 异常检测算法的评价·关键变量
原则上使用多元高斯分布时要求\(m≥10n\)

奇异的协方差矩阵

如果在实际应用过程中协方差矩阵\(Σ\)不可逆，有如下两种常见的可能：
1. 数据的量小于特征的数量 2. 冗余的特征：存在相同的特征，或者存在某个特征是其他若干个特征的线性组合（高度线性相关）的情况。