12.4. 协同过滤算法的优化

协同过滤算法的优化

向量化

设计一个大小为\(n_m × n_u\)的矩阵\(Y\)，其每一个元素表示用户\(j\)对电影\(i\)的评分\(y(i,j)\)。 由于预测的评分由\(θ^Tx\)给出，因此预测评分的矩阵能够表示为：
\[Y_{pre}=Θ^TX\] 其中\(X\)是所有电影的特征向量组成\(x\)的电影的特征矩阵，其每一行都是一部电影的特征向量。 \(Θ\)是所有用户倾向的特征向量\(θ\)组成的用户的特征矩阵，其每一行都是一个用户的特征向量。
协同过滤算法的向量化后的算法又称为低秩矩阵分解。

寻找相关内容

协同过滤算法能对每一个目标（比如电影、商品等等）都生成一个特征向量\(x^{(i)}∈R^n\)，两个目标\(i\)和\(j\)的类型相似在线性代数上的直观反映是两个目标的特征向量的欧氏距离很小： \[||x^{(i)}-x^{(j)}||\]
因此找到和目标\(i\)比较近的其他目标就能实现推荐与\(i\)内容相近的内容。

均值归一化

假设现在有一个用户没有对任何的电影评分，观察代价函数对其的影响：
\[J(θ^{(i)},x^{(j)})=\frac{1}{2}∑_{(i,j):r(i,j)=1}((θ^{(i)})^Tx^{(i)}-y^{(i,j)})^2+\frac{λ}{2}∑_{j=1}^{n_u}∑_{k=1}^n(θ_k^{(j)})^2+\frac{λ}{2}∑_{j=1}^{n_m}∑_{k=1}^n(x_k^{(i)})^2\]
可以发现，由于\(x\)是一个零向量，代价函数中只有\(θ\):的正则化项\(\frac{λ}{2}∑_{j=1}^{n_u}∑_{k=1}^n(θ_k^{(j)})^2\)对其有影响。
最小化这个代价函数，最终会得到这个用户的特征向量也是一个零向量，故预测对所有电影评分的结果全是0。或者如果一个用户给所有的电影评分都为0，推荐算法将不会很好地推荐内容。
均值归一化能够解决上述问题，
现在除了生成评分矩阵\(Y\)之外，另外设计一个均值向量\(μ\)用于储存每一部电影的平均得分。
现在将评分矩阵\(Y\)的每一行（也就是每个用户对同一部电影的评分）都减去平均得分。未评分的项（以\(?\)记）不做处理。

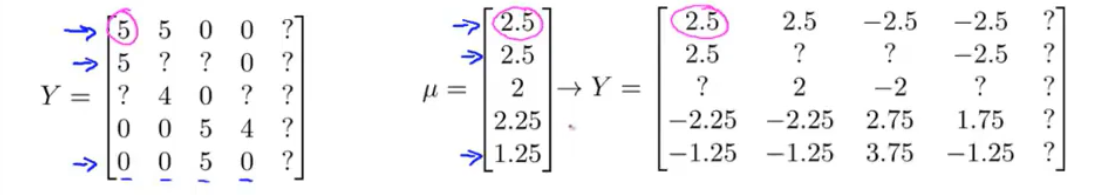
对新的评分矩阵\(Y_{norm}\)使用协同过滤算法：
现在用户\(j\)对电影\(i\)的评分需要补上之前减去的均值：
\[y_{pre}^{(i,j)}=(θ^{(j)})^T(x^{(i)})+μ_i\]
那么没有对任何电影评分的用户得到的预测评分将不再为0，而是反映所有人打分均值的\(μ_i\)。

同样的思路，假设有一部新上映的电影没有被任何人评价过，则可以采用列向量均值归一的方法：生成列向量的均值（同一个用户对所有电影的平均得分），用评分矩阵\(Y\)的每一列减去这个均值进行处理。
不过关心没有评分的用户比关心没有评分的电影要更为重要。因此列向量的均值归一化并不是必须的。