13.2. 随机梯度下降算法

随机梯度下降算法

在13.1. 中提到使用传统的梯度下降算法来最小化大数据集的代价函数计算量非常大，因此需要找到一种方式来改进现有的梯度下降算法。一种可行的方式是随机梯度下降算法（Stochastic gradient desent）。

回顾：线性回归的梯度下降算法

对于假设函数：\(h_θ(x)=∑_{j=0}^mθ_jx_j\)
其训练集的代价函数为：
\[J_{train}(θ)=\frac{1}{2m}(h_θ(x^{(i)})-y^{(i)})^2\]
使用梯度下降算法找到最小化\(J_{train}(θ)\)的参数\(θ\)，其内循环为：
\[θ_j:=θ_j-α\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\]
其中\(\frac{∂}{∂θ}J_{train}(θ)=\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\)
梯度下降算法通过不断地迭代求梯度找寻局部最小值，最终达到算法收敛。上述的梯度下降算法对整个数据集中的所有项求和，在一次下降迭代中需要同时考虑整个数据集中所有的数据，称为批量梯度下降算法（Batch gradient desent）。

随机梯度下降的思路

随机梯度下降算法在每一次迭代时不需要考虑所有的数据。
观察批量梯度下降算法，可以发现代价函数的本质实际上是衡量参数\(θ\)对每一个某个样本\((x^{(i)},y^{(i)})\)的拟合程度，再取平均值。因此代价函数\(J_{train}(θ)\)可以被分解为：
\[cost(θ,(x^{(i)},y^{(i)}))=\frac{1}{2}(h_θ(x^{(i)})-y^{(i)})^2\] 如之前所说，这一部分衡量的是参数\(θ\)在某个样本\((x^{(i)},y^{(i)})\)上的具体表现情况。
原来的代价函数可以改写为：
\[J_{train}(θ)=\frac{1}{m}cost(θ,(x^{(i)},y^{(i)}))\] 按照上文的理解方式，\(J_{train}(θ)\)可以看做是衡量参数\(θ\)对数据集整体的平均表现。
与批量梯度下降算法不同的是，随机梯度下降算法的每一次迭代只观察数据集中的一个样本\((x^{(i)},y^{(i)})\)，根据这一个样本的评价来缩小\(θ_j\)直到遍历完整个数据集。然后重复这一遍历数据集，分别以每个样本的评价来缩小\(θ_j\)的过程，直到\(θ_j\)达到收敛。

随机梯度下降算法的流程

1. 将整个数据集随机打乱排列
2. • 对于每一个样本，以这个样本的梯度来下降迭代\(θ_j\)：
     \[θ_j:=θ_j-α(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\] 其中\(\frac{∂}{∂θ_j}cost(θ,(x^{(i)},y^{(i)})=(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\)
     
   • 移动到下一个样本，重复上述过程，直到遍历完整个数据集。
     
3. 重复整个遍历过程，直到找到使得\(J_{train}(θ)\)取得最小值的\(θ_j\)。

注意随机梯度下降算法有两个嵌套的循环。一般来说，遍历1次数据集（最多不超过10次）能够使得算法达到收敛。

由于每次迭代只考虑一个样本而并非是整个数据集，因此随机梯度下降的计算量更小，收敛速度也更快。但是收敛的路径更为曲折。
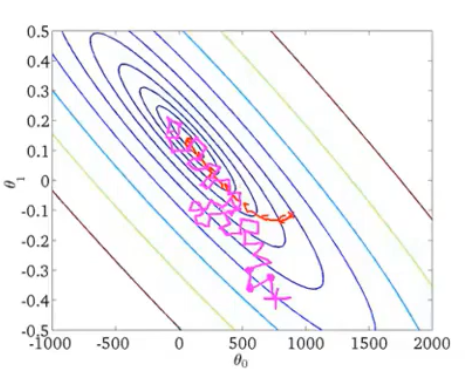
对比批量梯度下降，由于批量梯度下降每次迭代都需要找到全局（指整个数据集的求和项）极小值，因此批量梯度下降算法迭代的路线基本上始终是向着最小值收敛的（下图红线）。然而局部梯度下降算法收敛的路线更为曲折（下图洋红色线）。

调试随机梯度下降算法

绘制图像

在批量梯度下降中，可以绘制\(min_θJ(θ)-batch\)的图像1.4. 调试方法 θ:minJ(θ)-batch图像，或者是绘制\(J(θ)-batch\)的图像，根据图表来判断梯度下降是否收敛。但是，在大规模的训练集的情况下，要周期性地暂停学习并且求得此时的\(J(θ)\)或者是使得\(J(θ)\)最小化的\(θ\)的值所带来的计算量非常地大。因此需要其他的调试方法应用于大数据学习时的随机梯度下降算法。
对于随机梯度下降算法，在计算当前样本的\(cost(θ,(x^{(i)},y^{(i)})\)后,在更新\(θ\)之前，直接输出此时的\(cost\)函数值。
在固定周期的迭代次数（比如每1000次迭代）后，计算这个迭代周期内这些样本的\(cost\)函数值的平均值，通过观察绘制的图来判断梯度下降算法是否达到了收敛。
#### 观察周期的设置
迭代周期设置的越大，迭代过程中的噪声就越不明显，曲线越平滑。

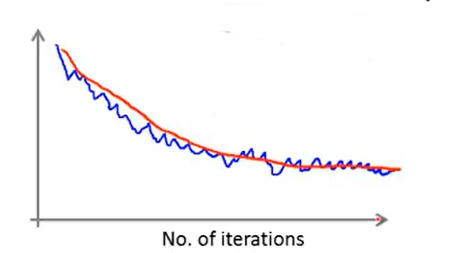
如上图，蓝色线的所观察的周期要比红色线所观察的周期更短。
如果观察的周期设置的太短，则有可能观察不出下降的趋势，如下图所示。

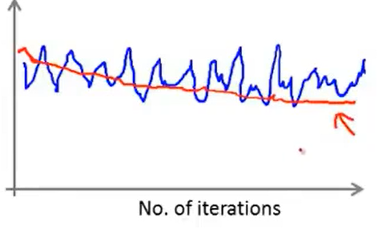
当设定比较大的周期进行观察，如果此时下降程度仍然不明显，表明算法几乎没有学习数据集，需要对算法进行进一步的调整。

学习率的影响

在这两种算法中，学习率越小，算法收敛的越慢，但是最后收敛的结果可能会更小。

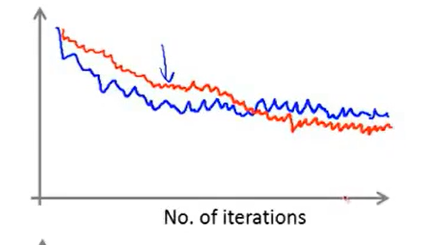
如上图，图中蓝色线的学习率比红色线的学习率更大。
如果图像呈上升趋势，那么表明算法发散，则需要设置更小的学习率。

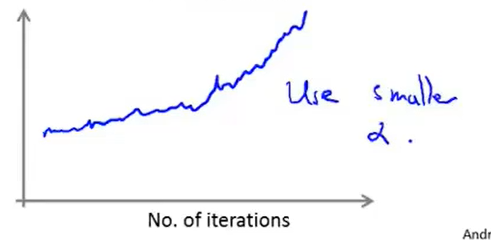
也可以令学习率随着迭代次数的增加而减小，例如令： \[\alpha=\frac{c_1}{IterationNumber + c_2}\] 其中\(c_1\)和\(c_2\)是两个常数。
随着不断地靠近全局最小值，通过减小学习率，迫使算法收敛而非在最小值附近徘徊。 但是通常不需要这样做便能有非常好的效果了——对\(α\)进行调整所耗费的计算通常不值得。