13.5. 并行计算（减少映射）

并行计算（减少映射）

减少映射（Map-reduce）是第二种能够在大规模机器学习中用于减少计算量的算法。本质上，减少映射的工作就是将机器学习算法进行并行化处理，使得多个计算机共同、同时承担梯度下降算法中的一部分计算内容以缩短计算时间和单台计算机的计算量。减少映射与随机梯度下降一样重要。
机器学习算法能够被减少映射的关键在于算法本身或者是其中的某些步骤能够以求和的方式表示。事实上，大规模机器学习的主要问题也来自于求和项的计算量过于庞大，并且大部分的机器学习算法都拥有求和项，因此可被减少映射。

梯度下降算法的并行化

减少映射的思想基础来源于批量梯度下降算法。根据批量梯度下降的更新公式：
\[θ_j:=θ_j-α\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\]
此时如果用多台计算机平均负担求和项（或者说是代价函数的偏导项）\(∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\)。比如如果有4台计算机，这四台计算机分别计算数据集中\(\frac{m}{4}\)份数据的求和项，最后再将这些计算结果放入一个中心计算机进行更新公式的计算。

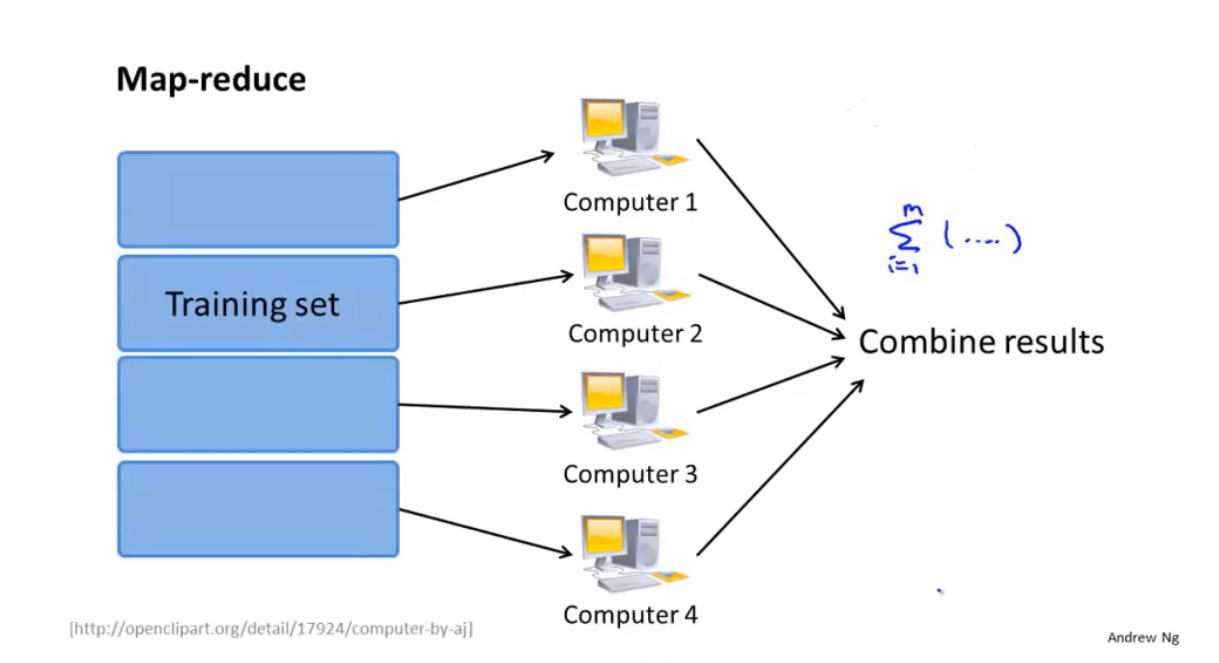
逻辑回归的并行化

逻辑回归的代价函数公式：
\[J_{train}(θ)=-\frac{1}{m}[∑_{i=1}^m y^{(i)} log⁡(h_θ(x^{(i)} ))+(1−y^{(i)}) log(1−h_θ (x^{(i)}))]\] 同样地，逻辑回归的代价函数中求和项也可以分配给多台计算机承担。
而且逻辑回归的代价函数的偏导项和线性回归一样：
\[\frac{∂}{∂θ_j}J_{train}(θ)=\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x_j^{(i)}\] 其中的求和项也可以被并行化处理，最终以便于使用梯度下降算法。
这些求和项在不同的计算机上被计算出来后，传入中央计算机，并执行求和和求和之外的其他计算。

多核计算

由于GPU或者CPU的多核计算功能，并行化计算也可以在单机上运行。类似地，训练集被划分然后送入CPU中不同的处理核心中进行计算，最后整合结果。

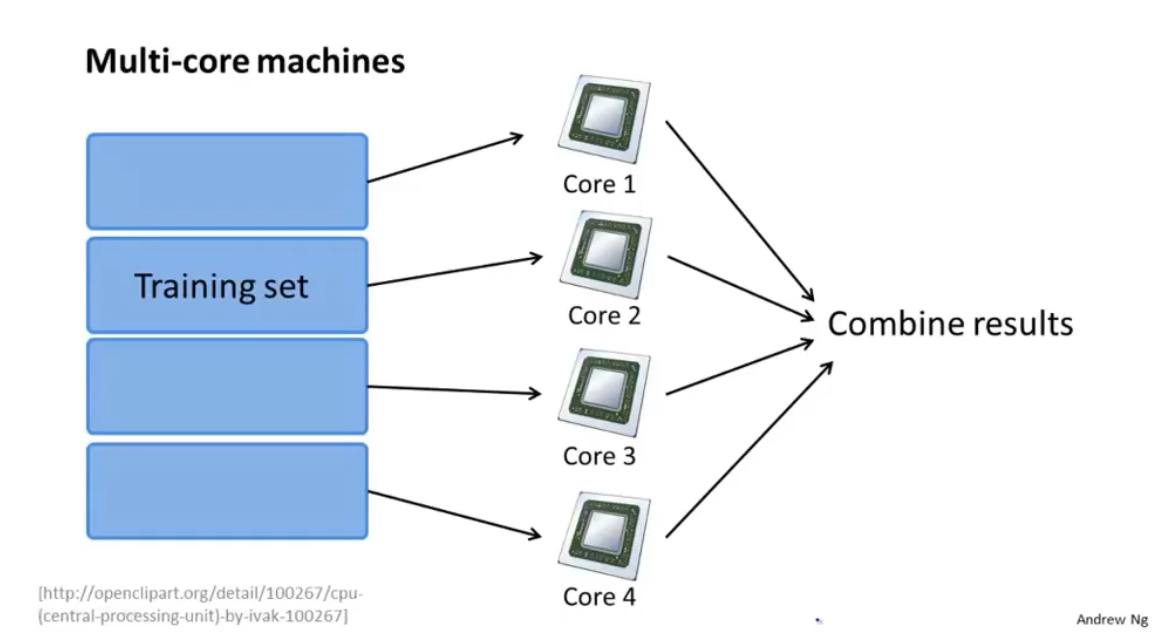
有些机器学习库或者线性代数库可以自动地将算法矩阵化后做并行化处理，因此不需要人为地设置减少映射。