可靠性工程-知识点总结

本文是BUL EE2634 Digital Systems Design and Reliability Engineering 可靠性工程部分的知识点总结。

可靠性工程的衡量指标

可靠性术语-德州仪器：https://www.ti.com.cn/zh-cn/support-quality/reliability/reliability-terminology.html

产品质量、性能和可靠性是可靠性工程的三个重要因素。此外产品的可维护性，可用性等指标也与可靠性工程有关。

质量

产品或者服务的质量（Quality）可以定义为：产品或服务满足用户给定需求的全部功能和特性的能力。
产品的质量与制造产品时所用的主要材料和工艺（craftsmanship）有关。

有如下的因素可以影响产品对目标值的实现度，即产品质量：
- 生产噪声：在制造过程中因为制造差异和缺陷而导致的产品个体差异。
- 内部噪声：在使用过程中产品某些性质的改变，比如磨损，生锈等等。
- 外部噪声：环境因素（比如温度、湿度、尘埃等等）和用户的使用方法。

性能

产品的性能(Performance)通常用产品执行其预期功能的程度来衡量。

可靠性

可靠性(Reliability)通常表征产品未来的性能，是一个随机变量。它的定义需要由性能条件，环境条件，时间范围对其限制。
某个产品或系统的可靠性可以定义为在特定时间内，在生命周期条件下能够如期表现其性能的能力。

生命周期条件指产品在整个生命周期（生产、运输、储存、使用）中能够正常运行的环境条件。

衡量产品可靠性的因素

对同一个产品，其可靠性并不是唯一的。某个产品的可靠性主要依据四个因素进行衡量和定义：
- 对“预期功能”的定义 - 对“产品期望性能”（Satisfactory performance）的定义 - 使用条件和环境条件 - 时间

可靠性与产品生命周期

整个产品的生命周期中都会涉及到有关可靠性的活动:

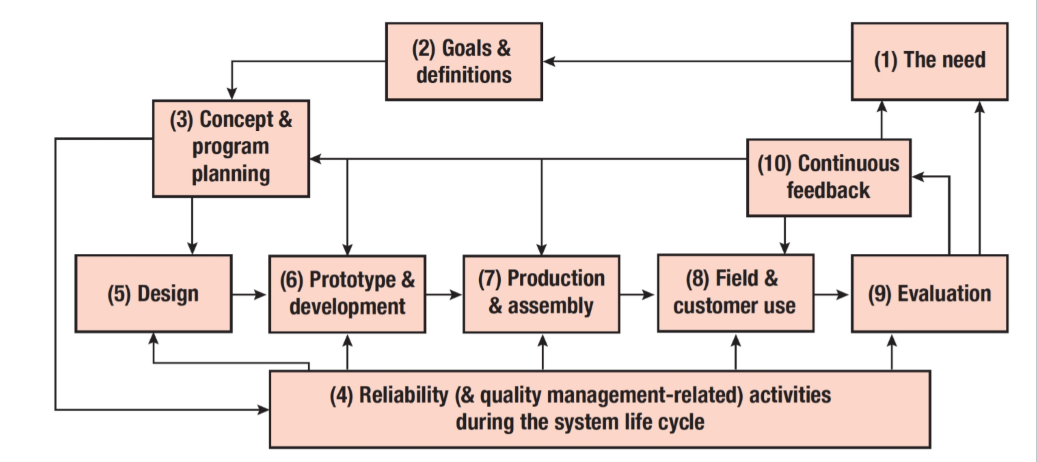
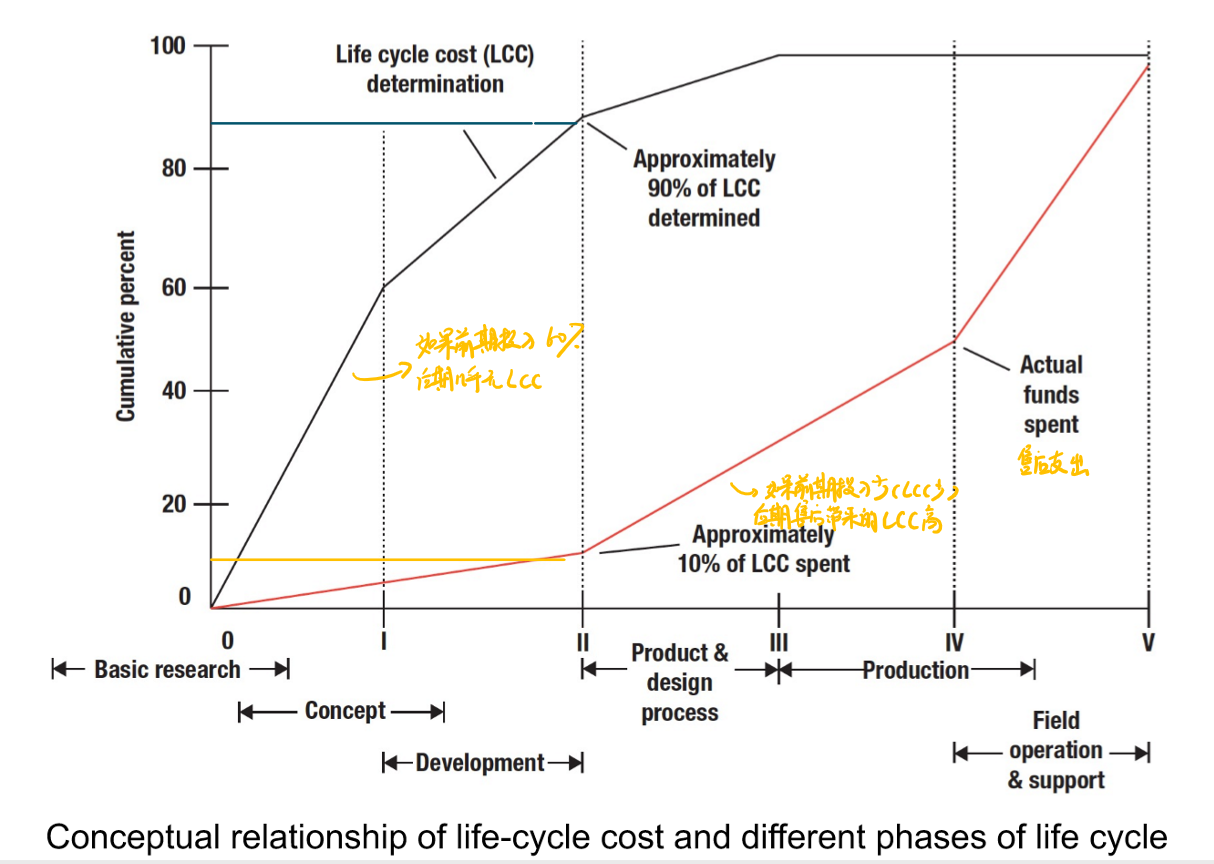
在整个产品生命周期中的投入方式有两种假设：一种是在产品周期的前期对可靠性的投入较大，那么在后期就可以对产品的可靠性投入较少。如果在产品周期的前期对对可靠性的投入较少，那么在生命周期的后期由于产品出问题的概率较大，因此在后期对可靠性的投入（比如售后和维修支出）需要较多，两种假设可以用下图表示：

可靠性失效的后果

对于不同的产品和失效方式，产品可靠性失效的后果可能影响不大，也可能导致灾难性的后果。常见的失效后果包括： - 财产损失 - 人员伤亡 - 无形成本损失 - 公信力损失 - ...

可维护性（Maintainability）

产品的可维护性定义为：在规定的使用条件下，使用规定的程序和资源进行维护时，产品能够通过维修恢复到能够履行其所需功能的状态的能力。 #### 维护的类别 - 修复性维护（Corrective Maintenance）
故障发生后对产品进行的维护，是一种事后维护。
- 预防性维护（Preventive Maintenance）
每隔一段时间或按照规定的标准进行的维护，目的是减少发生失效的概率。
- 预测性维护（Predictive Based Maintenance）
是以状态为依据(Condition Based)的维护，在机器运行时，对它的主要（或需要）部位进行定期（或连续）的状态监测和故障诊断，判定产品所处的状态，预测产品状态未来的发展趋势，依据产品的状态发展趋势和可能的故障模式，预先制定预测性维护计划，确定机器应该修理的时间、内容、方式和必需的技术和物资支持。

维护的衡量指标

可维护性通过修复所需要的时间间隔进行衡量。

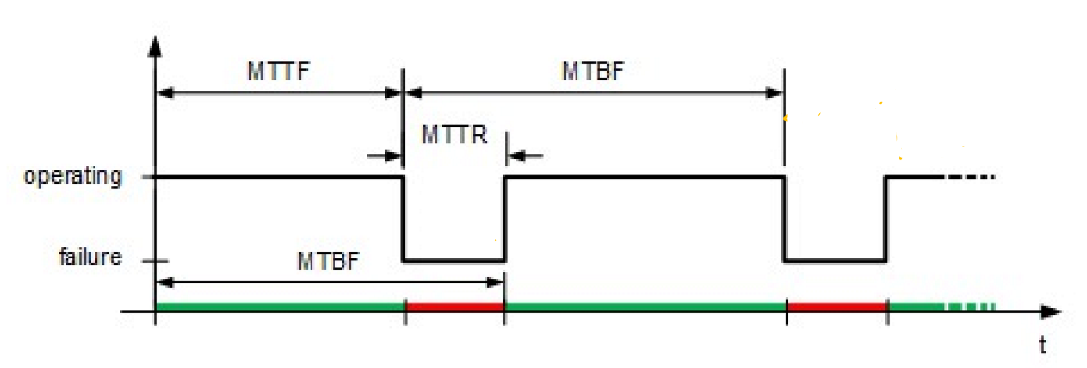
• MTTR（Mean Time To Repair）
  平均维护所需时间，是系统的宕机时间（Downtime）。
  > 宕机时间又指系统因为干扰而不能正常工作的时间。

  \[MTTR=\frac{总维护时间}{维护次数}\]

• MTTF（Mean Time To Faliure）
  平均故障时间，指系统维修好后到下一次出现故障的平均时间，是系统的正常工作/上线时间（Uptime）。
  > 上线时间又指系统正常工作的时间。

• MTBF（Mean Time Between Failures）
  平均故障间隔时间，指两次故障发生的平均间隔时间，是系统的工作时间。
  三者满足如下关系：
  \[MTBF=MTTR+MTTF\]

• 可用性
  定义可用性（Availability）为系统的上线时间与系统总工作时间之比：
  \[A=\frac{MTTF}{MTBF}=\frac{MTTF}{MTTF+MTTR}\] 对于不可修复性系统而言，系统一旦宕机，不可修复：\(A=\frac{MTTF}{MTTR}=1\)。

可靠性工程的统计分析

质量、性能和可靠性的统计定义

产品的可靠性估计量可以通过在某时刻\(t\)下采样得到，具体而言： 产品的可靠性估计量可以用某时刻\(t\)下采样中的良品数量与样品总数之比进行表示：
\[\hat{R(t)}=\frac{n_s(t)}{n_0}=1-\hat{F(t)}\] 其中\(\hat{F(t)}=\frac{n_f}{n_0}\)表示失效率(Failure rate)的估计量，定义与可靠性相反。
如果失效率的概率密度函数用\(f(t)\)表示，那么失效率的概率积累函数为：
\[F(t)=\int_0^tf(τ)dτ\] 其物理意义是在\(t\)时刻下失效产品占产品总数的比例。

失效率的概率密度函数必须满足全域积分为1(\(∫f(t)dt=1\))的条件。

\(B_α\)表示：\(F(B_α)=\frac{α}{100}\)

那么可靠性的概率积累函数表示为：
\[R(t)=1-F(t)=\int_t^∞f(τ)dτ\] 其物理意义是在\(t\)时刻下存留产品（未失效）占产品总数的比例。

已知\(t_1\)时刻下的可靠性\(R(t,t_1)\)，在\(t\)时刻（\(t>t_1\)）的可靠性\(R(t,t_1)\):
\[R(t,t_1)=\frac{R(t+t_1)}{R(t_1)}\]

风险率

风险率（Hazard Rate）是某一时刻\(t\)下，单位时间失效产品数与存留产品数之比。风险率可以理解为某一时刻下的失效率，表示为：
\[h(t)=\frac{f(t)}{R(t)}\] 风险率可以用一段时间失效产品数与存留产品数之比除以时间估计：
\[\hat{h}(t)=\frac{N_f}{N_0Δt}\] 风险率是产品失效的相对表征，因此风险率与样本数量大小无关。
可靠性和风险率的关系为：
\[R(t)=e^{-\int_0^th(τ)dτ}\]

澡盆曲线/寿命特性曲线

理想的产品风险率曲线应当如下图所示，称为澡盆曲线/寿命特性曲线。

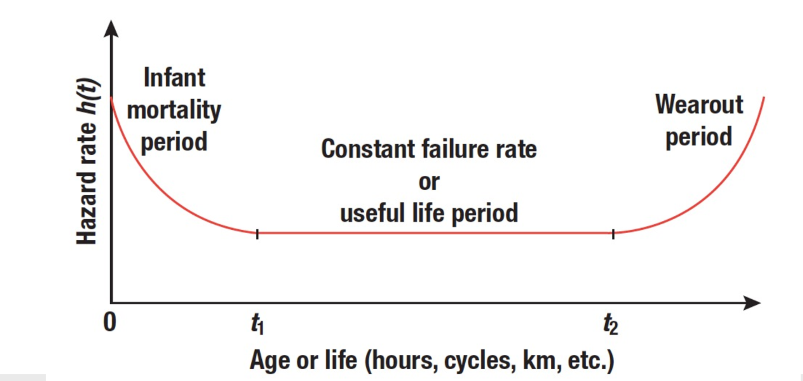
澡盆曲线对应的可靠性曲线如图所示：

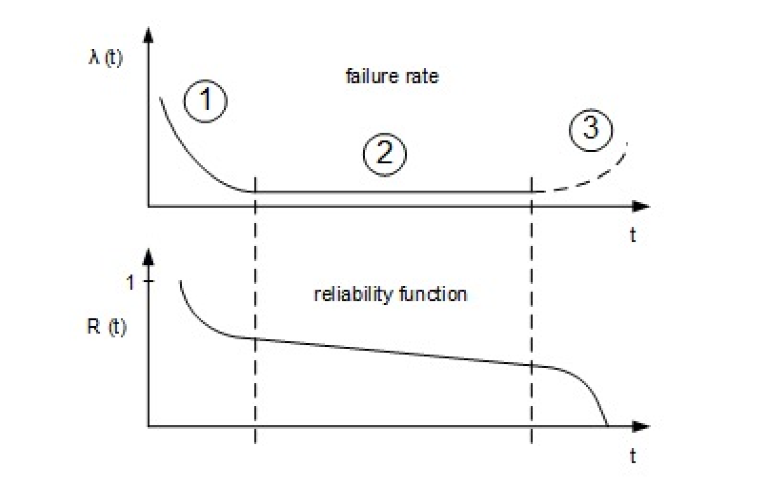
如图，一般把产品从投产起至严重磨损后的全过程划分为三个时期，即初期故障期、偶发故障期与磨损故障期。
- 初期故障期(Infant Mortality Period)
产品在投产后的一段时间内，一些可靠性较差的产品会立即失效，因此初期故障期产品总体的风险率很高，随时间逐步下降。
> 某些厂家会在出厂后增加一段“腐蚀期”以筛选出可靠性较差的产品，再投入销售。

• 偶发故障期（Useful Life Period）
  在用户使用的前期和中期，产品比较稳定，不容易出现失效，在此期间的风险率较低。

• 磨损故障期（Wear-out Period）
  在用户使用末期，产品随着时间和使用次数的增加而磨损，出现失效的概率大幅度增加。可以采取维护或者更换的方式延长产品总体的可靠性。

可修复性的统计定义

可修复性可以表示为失效率的统计均值：
\[MTTF=\int_0^∞tf(t)dt=\int_0^∞R(t)dt\]

离散分布特征

可靠性可以看做是未来的系统质量，可以用随机变量表示。
离散分布有伯努利分布、二项分布和泊松分布。

分布类型	概率密度/积累分布函数	期望	方差	备注
伯努利分布	\(f(k)=p^kq^{1-k}\)	\(μ=p\)	\(σ^2=p(1-p)\)
二项分布	\(f(k)=C_k^mp^kq^{m-k}\) \(F(k)=∑_{i=0}^kC_i^mp^iq^{(m-i)}\)	\(μ=mp\)	\(σ^2=mp(1-p)\)	\(m\)：所有可能事件数
泊松分布	\(f(k)=\frac{μ^k}{k!}e^{-μ}\)	\(μ=mp\)	\(σ^2=mp\)	\(m\)：所有可能事件数

连续分布特征

威布尔分布（Weibull Distribution）

威布尔分布是最常见的一种用于拟合风险率的曲线，其概率密度函数为：
\[f(t)=βη^{-β}(t-γ)^{β-1}e^{-(\frac{t-γ}{η})^β}\] 其中，\(β>0\)是形状参数，\(η>0\)是放大尺度，\(γ\)是时移尺度，通常等于0。
\[R(t)=∫_t^∞f(t)dt=e^{-(\frac{t-γ}{η})^β}\] 其均值为： \[ηΓ(1+\frac{1}{β})\] 其方差为：
\[η^2\left(Γ(1+\frac{2}{β})-Γ^2(1+\frac{1}{β}))\right)\]

指数分布（Exponential Distribution）

指数分布是威布尔分布在\(β=1\)，\(γ=0\) 时的特殊情况：
\[f(t)=λ_0e^{-λ_0t},λ_0=\frac{1}{η},t≥0\] 其均值为\(\frac{1}{λ_0}\)，方差为\((\frac{1}{λ_0})^2\)。
可靠性表示为：
\[R(t)=e^{-λ_0t}\] 风险率表示为：
\[h(t)=λ_0\]

正态分布（Gaussian/Normal Distribution）和对数正态分布（Log-normal Distribution）

正态分布的概率密度函数为：
\[f(t)=\frac{1}{\sqrt{2π}σ}e^{-\frac{(t-μ)^2}{2σ^2}}\] 当\(μ=0,σ^2=1\)时退化为标准正态分布：
\[ϕ(t)=\frac{1}{\sqrt{2π}}e^{-\frac{t^2}{2}}\] 任何均值为\(μ\)，方差为\(σ^2\)的正态分布都可以转化为标准正态分布，来求概率积累函数：
\[F(t)=Φ(\frac{t-μ}{σ})\] \[f(t)=\frac{ϕ(\frac{t-μ}{σ})}{σ}\] 标准正态分布是一个以1对称的函数：
\[Φ(-z)=1-Φ(z)\] 其中\(Φ(\frac{t-μ}{σ})\)可以在标准正态分布表中找到对应的值。

对数正态分布中，\(t:=lnt\)，其余性质与正态分布完全相同。
其均值为；\(MTTF=e^{μ+\frac{σ^2}{2}}\)。
风险率表示为：
\[h(t)=\frac{ϕ(\frac{lnt-μ}{σ})}{σtR(t)}\]

伽玛分布（Gamma Distribution）

伽玛分布的概率密度函数*：
\[f(t)=\frac{λ^η}{Γ(η)}t^{η-1}e^{-λt}\] 其中\(η\)是其形状参数，\(λ\)是尺度参数，\(Γ(η)\)由伽马函数通过查表得到，伽马函数满足：
\[Γ(n+1)=nΓ(n),n>0\]

可靠性分析数据和数据来源

数据类型

技术数据

数据中指定了通道、子系统、各部分的工作原理。 #### 操作数据 数据中指定了操作模式、操作环境和操作条件。

可靠性数据

数据中给出了失效率，MTTF，或者是其他能够估计可靠性的数据。
可靠性数据包括如下五类：
- 泛用性数据（Generic Data）
由各种组织收集并公开的数据。
这些数据的时效性可能较低，当新环境/功能/操作条件引入时，这些数据可能准确率不高，因此需要对未注册数据进行处理。
处理的方法是用已知的未注册数据中的失效率\(λ_B\)中根据现有所有影响因子\(δ_i\)赋权后得到当前的失效率\(λ_p\):
\[λ_P=λ_B\sum_{i=1}^kw_iσ_i\] 其中\(σ_i\)是影响失效率的影响因子（比如温度、湿度、测试时长等等），\(w_i\)是影响因子对应的权重，表示每个影响因子的对失效率的相对影响能力，并对其归一化：\(∑w_i=1\)。
- 制造商数据
由制造商提供的数据，包括实验室测试，失效或者失效率估计等等。
- 用户数据
通过特定用户收集的数据。
- 专家判断
基于专家观点和经验提出的数据，可在在刚开始运行系统/新功能时可分析数据量不多的情况下使用。

测试和维护数据

与维护和测试相关的数据，比如观察时间，平均维修时间等等。

这四类数据对于可靠性分析的作用如下图所示：

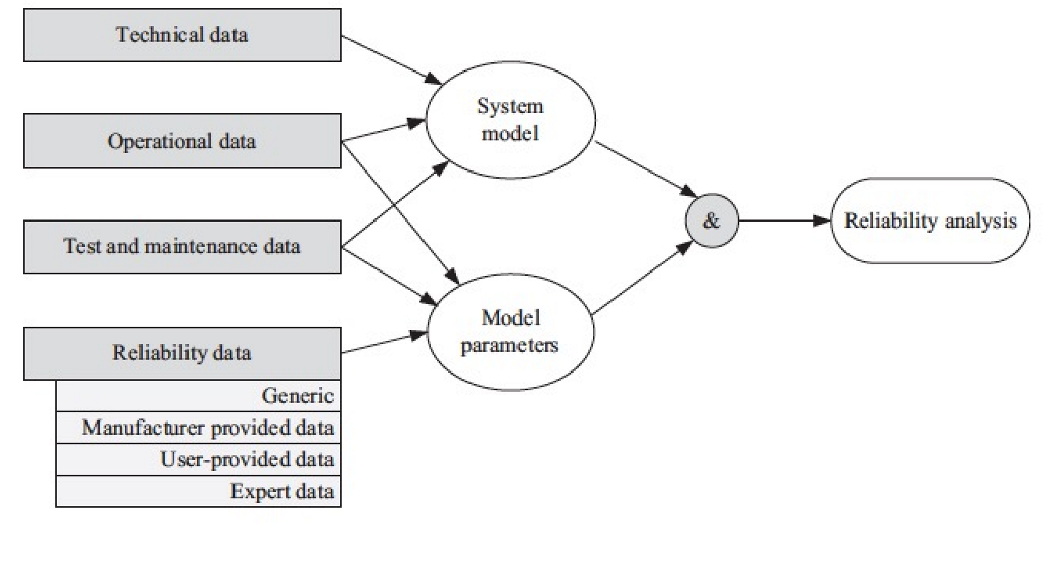
删失（Censoring）

删失数据是指在观察或试验中,由于人力或其他原因未能观察到目标事件发生，因而得到的数据。

6σ原则

6σ原则是一种经管流程，通过持续的流程改进来提高业务的最低水准。
6σ原则的目的是将零缺陷(Zero-defects)管理流程应用于组织中的每一个流程/产品当中。

生命周期档案

产品的生命周期档案（Life-cycle loads）中包括了商品在生命周期的每一个阶段中可能影响产品生命周期的因素。

产品的生命周期

产品的生命周期包括：
制造和装配、测试、修改（Rework）、仓储、运输、运行、维修（Repair）、维护（Maintenance）。
#### 生命周期负荷 生命周期负荷（Life-cycle loads）指能够影响产品生命周期的因素，通常分为五大类：
- 热学负荷（Thermal）：如温度区间、温度周期、温度梯度等。 - 力学负荷（Mechanical）：如压力、震动、声级（Acoustic level）等。 - 化学负荷（Chemical）： 如臭氧浓度（Ozone）、惰性（Inert）环境、污染（contamination）等。
- 物理学负荷（Physical）：如辐射、磁场干扰、纬度等。
- 运行负荷（Operational）：如热耗、功率、电流、电压等。

常见的生命周期负荷对产品的影响

• 温度
  1. 改变产品材料的性质。
  2. 改变化学反应（如腐蚀、生锈）的速率。
• 震动
  1. 导致产品发生线性或非线性的移动。
     
  2. 导致由于产品运动而造成的额外的机械能耗散或存储。
     
• 太阳辐射
  1. 对产品有紫外线和其他可能造成产品破坏的射线辐射。
     
  2. 使产品和环境温度上升。
     
• 电磁辐射
  
• 化学品和化学因素
  1. 使材料腐蚀（corrode）和变质（deteriorate）。
     
  2. 由于生物化学反应，产品容易发生老化和生物（比如细菌）附着。
     
• 尘埃
  1. 进入机械结构中损伤产品结构。
     
  2. 覆盖在元器件表面，影响其散热。
     > 防范措施分为主动（通风、使用风扇或者空气净化器）和被动（植树）两种。
     
• 电压
  1. 过高的电压导致产品过载、金属熔化、断路和断路。
     
  2. 长期高电压导致产品氧化（Oxide breakdown）。

量化估计生命周期负荷的方法

在可靠性分析中，生命周期负荷需要被量化估计，具体的方法包括：
1. 市场调研/查找标准数据
2. 监测生命周期负荷
3. 试验记录/失效记录/售后记录
4. 相同零部件的历史量化数据

可靠性试验

可靠性试验（Reliability Testing）的目的是：
1. 确定安全使用期限。
2. 确认产品规格是否符合预期。
3. 确定产品的失效模式。
4. 测试某一部件或系统超出标准使用范围时的运行稳定性。

完整寿命试验

完整寿命试验（Full-life Testing）将产品在其整个生命周期种对其施加预测好的正常使用下的应力（Stress），观察产品在整个寿命周期中的变化。其缺点是这样的寿命测试需要持续相当长的时间，甚至需要24小时/7天全天候持续运行测试。

加速寿命试验

加速寿命试验（Accelerated Life Testing,ALT）是一种决定产品寿命终止期限（end-of-life）和预测其失效模式的方法。其在短时间内通过增加应力来模拟产品在生命周期中受到的磨损情况，以预测在正常工作条件或储存条件下的可靠性。
加速寿命试验会增加产品在整个生命周期的风险率，但不改变受试产品在整个生命周期的失效分布。

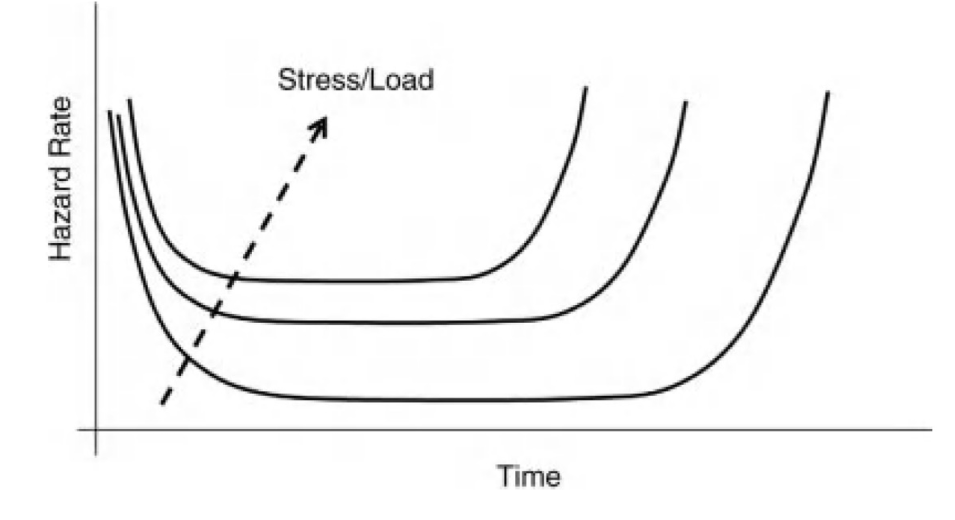
加速寿命实验的前提条件是测试前需要对产品的失效机制（Failure Mechanisms）有足够的了解，并且测试目的是明确的探究指定因素对产品寿命的影响。

失效机制

失效机制是力学、化学、电学等条件导致故障的过程。潜在的失效机制是根据失效模式和原因、载荷和材料确定的。通常，失效机制分为“磨损”（Wearout）和“过载”（Overstress）两类。
- 磨损 磨损是指应力长时间积累对产品造成的损坏。
- 过载 过载是指单一的，超出了材料承受限制的应力对产品造成的损坏。

环境应力筛选

环境应力筛选(Environmental Stress Screening,ESS)是为发现和排除不良产品和防止出现早期失效，在环境应力下所做的一系列试验。它的意义就是筛选产品，把通过不能用常规检验或试验的方法查出的缺陷，暴露出来。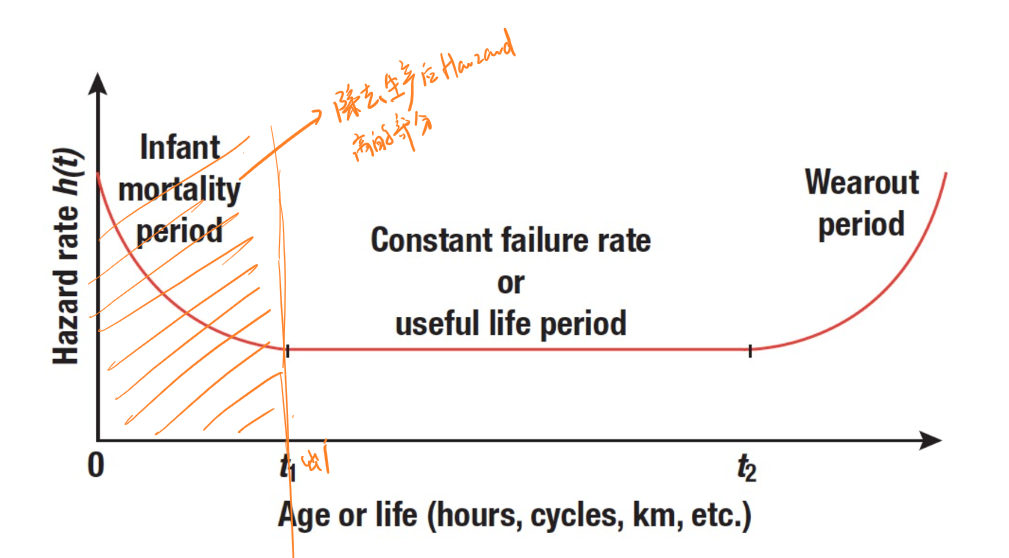

电磁兼容试验

电磁兼容性 (Electro-Magnetic Compatibility,EMC) 是指产品在它本身的电磁环境中，能够正常工作且不会产生让其它在此环境中的设备难以忍受的电磁干扰的性质。 电磁兼容试验（Electromagnetic Compatibility Screening Testing,EMC Testing）的目的是为了测试产品的这一性质。
常见的电磁兼容试验项目包括：辐射骚扰测试（Radiated Emission）和传导骚扰测试（Conducted Emission）等等。

失效分析方法

故障树

系统中的每一个部分的失效和整个系统失效之间的关系可以用布尔运算表达。故障树（Faulty tree）通过树形结构表示这一布尔运算式。基本的树形结构表达如下图所示：

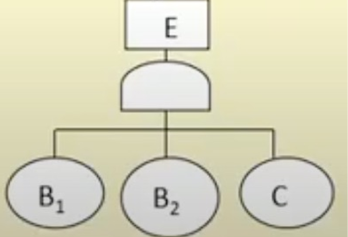
对于和事件，其发生概率为：
\[P(I)=P(A)+P(B)-P(A)P(B)\] 对于积事件，其发生概率为：
\[P(I)=P(A)P(B)\]

需要注意的是，这样的树形结构中的下层结构中所有子部分的失效率之和应当为1。

故障树的基本分析思路是：
1. 从下向上分析，从最低层级的子树分析，写出子树的布尔运算式。
2. 分析高层级的树，写出其布尔运算式，并将子树的布尔运算式带入。
3. 使用运算律化简整个系统的布尔运算式。

可靠性框图

可靠性框图是另一种表达系统中的每一个部分的失效和整个系统失效之间的关系的方法，其在系统框图中加入了每个部分的可靠性概率（即正常工作的概率）。
基本的系统结构有并联和串联两种。
对于串联系统，系统正常工作的条件是每个部分都能够正常工作，每个部分正常工作的概率为\(P_{i|R}\)，\(P_{i|R}\)表示部分\(i\)的可靠性概率，因此串联系统的可靠性概率为：
\[P_R=∏_i P_{i|R}\]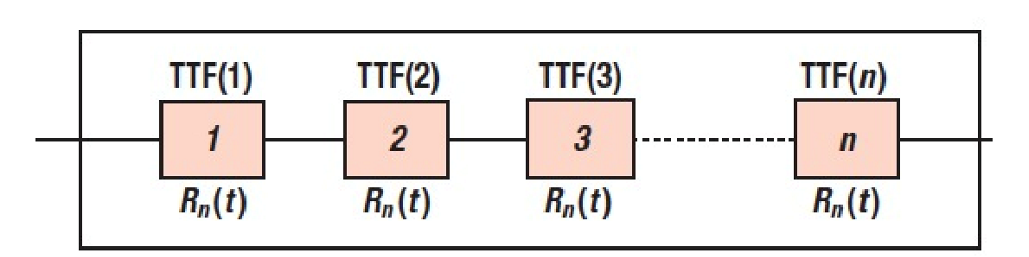

对于并联系统，系统正常工作的条件是每个部分都能够正常工作，即每个部分都不会发生失效，每个部分发生失效的概率为\(P_{i|f}=1-P_{i|R}\)，整个并联系统的失效概率为\(P_f=∏_i1-P_{i|R}\)，根据\(1-P_f=P_R\)，整个系统的可靠性概率为：
\[P_R=1-\left(∏_i1-P_{i|R}\right)\]