一种应用于细胞式生产的聚类方法

Machine-Component Group Formation in Group Technology. John R King. 1979. Effective clustering method for group thechnology problems: a short communication. Tamal Ghosh et al. e-Journal of Science and Technology, 2011.

问题动机

细胞生产方式（Cell Production/Cell Manufacturing）又名细胞式生产，单元生产方式或者单机生产方式，这是一种自律分散型生产方式，它是指多个独立的制造生产线根据生产的产品、环境和人员的不同，配置不同的顺序进行生产。在细胞式生产方式中，每条生产线就是一个独立的“细胞”，遵循周密、严格的生产计划，承担不同的生产任务。一个产品在各个“细胞”中分别进行加工，最终完成一个成品的生产。
聚类可以根据每个生产流程所需要的部件和生产机器，对生产进行细胞化，提高工厂的生产效率。

方法论

本文中提出的应用于细胞式生产的聚类方法是一种基于矩阵的聚类方法。这种聚类算法的过程如下：
在生产中，混淆矩阵的列表示某个零部件(parts)，矩阵的行表示生产该零件所需要的机器。矩阵内元素的值为二进制：如果某个元素的值为0，代表对应零件不需要这个机器。反之则代表需要这个（机器，部件）。依照这个规则建立事件矩阵。
通过重排序，最终矩阵中的“1”会聚集形成某些群落，代表形成了一个细胞(cell)。理想情况下，所有的细胞的群落形态都应该是矩形，但是有一些无法被聚类的“1”和“0”会导致细胞形态不规则。记与某个细胞相邻的使细胞形态不规整的“1”（凸出的“1”）为特例元素(EE,exceptional elements)，凹陷的“0”为空隙（void）。

首先，对于每一行（每个机器）形成的数列\(\bf{M_k}\)，使用皮尔森公式检验\(\bf{M_k}\)与其他每个机器数列\(\bf{M_m}\)的相关性：
\[r=\frac{\sum_{i=1}^n(m_{mi}-\overline{m_m})(m_{ki}-\overline{m_k})}{\sqrt{\sum_{i=1}^n(m_{mi}-\overline{m_m})^2}\sqrt{(m_{ki}-\overline{m_k})^2}}=\frac{n∑_{i=1}^nm_{mi}m_{ki}-∑_{i=1}^nm_{ki}∑_{i=1}^nm_{mi}}{\sqrt{n∑_{i=1}^nm_i^2-(∑_{i=1}^nm_i)^2}\sqrt{n∑_{i=1}^nm_k^2-(∑_{i=1}^nm_k)^2}}\] 定义两者的相似度可以表示为：
\[S=\frac{r+1}{2}\] 两者的距离定义为：
\[D=1-r\] 那么由此可以建立矩阵表示每一个机器\(\bf{M_k}\)到其他所有机器的距离。

比如对于如下的事件矩阵：

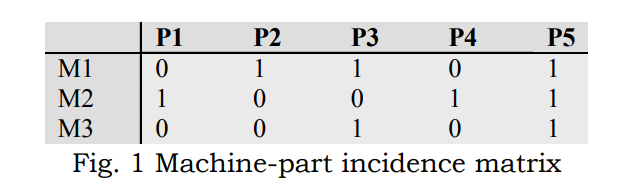
例如计算\(\bf{M_1}=[0,1,1,0,1]\)和\(\bf{M_2}=[1,0,0,1,1]\)，二者的皮尔森系数根据公式计算得到-0.667.
两者的距离为1.667.
可以得到距离矩阵：

从这个距离矩阵中可以发现\(M_1\)和\(M_3\)到\(M_2\)的距离比较接近，因此将\(\bf{M_1}\)和\(\bf{M_3}\)聚类为一个细胞，定义由群落\(p\)和\(q\)聚类后的群落\(r\)到另外某个群落\(s\)的距离为：
\[d(r,s)=\frac{d(p,s)+d(q,s)}{2}\]

那么由\(M_1\)和\(M_3\)形成的细胞到\(M_2\)的距离为：
\[d((1,3),2)=\frac{d(1,2)+d(3,2)}{2}=1.417\]

接着决定细胞中所使用的部件，定义部件\(j\)对细胞\(c\)的部件系数\(D{jc}\)为： \[D_{cj}=\frac{m_{cj}}{k_c}×\frac{m_{cj}}{n_j}×\frac{1}{v}\] 其中\(\frac{m_{cj}}{k_c}\)为使用部件\(j\)的机器在整个细胞\(c\)中的机器数量占比；
\(\frac{m_{cj}}{n_j}\)表示使用部件\(j\)的机器在所有机器中的数量占比；
\(v\)为这个细胞的空隙数。
计算上述例子中每一个部件对\((M_1,M_3)\)形成的细胞Cell1和\(M_2\)单独形成的Cell2的部件系数，得到下表：

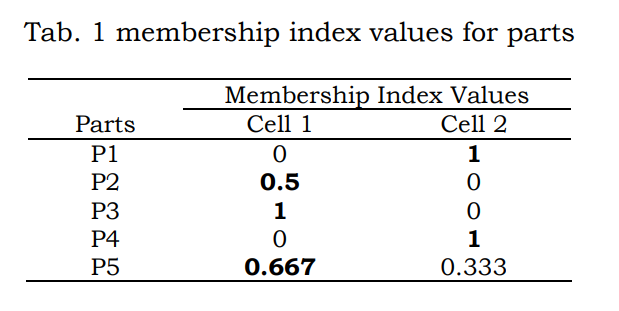
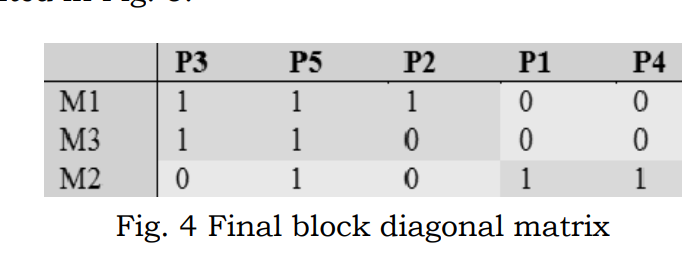
可以发现，对细胞1，部件2，3，5的部件系数较高；对细胞2，部件1，4的部件系数较高。因此聚类结果为部件2，3，5属于细胞1，部件1，4属于细胞2.

效果验证

聚类的效果验证可以由聚类效率表示：
\[τ=\frac{E-E_e}{E+E_v}\] \(E\)为整个矩阵中1的数量；\(E_e\)为整个矩阵中例外元素的数量，\(E_v\)为整个矩阵中空隙的数量。
聚类结果中例外元素和空隙的数量都要尽可能小才能表明聚类效果越好，因此\(τ\)越接近于1表明聚类效果越好。