灵敏度分析方法
本文最后更新于 2025年4月25日 晚上
灵敏度分析方法
Sensitivity analysis approaches applied to systems biology models, Zhike Zi, IET Systems Biology, 2011.
问题动机
在复杂系统分析时,一些系统的参数十分复杂甚至不能通过实验进行测量,还有一些参数在不同的实验条件下有非常大的变化。这些参数的复杂性和多变性为系统建模造成了困难。灵敏度/敏感度分析(sensitivity anlysis)可以量化来自系统输入的变化对输出变化程度的影响。具体而言,通过灵敏度分析可以知道:
- 系统输出对于每个输入变化的鲁棒性。
- 检验一个模型的预测结果是否与假设有关,并指导参数估计和实验设计。
- 通过量化模型输出和输入的相关性,去掉系数灵敏度很小的输入,重点考虑灵敏度系数较大的输入。这样就可以大大降低模型的复杂度。
另外,下述的所有系统模型都指系统的微分方程(ODE, ordinary differential equation),但是下述的这些灵敏度的分析方法也适用于其他形式的系统模型。
灵敏度的类型
系统灵敏度有两种类型:局部灵敏度(local sensitivity)和全局灵敏度(global sensitivity)。
局部灵敏度
局部灵敏度用于表示某个输入的、非常微小的变化可以导致输出变化的程度:如果某个输入非常小的变化可以引起巨大的输出端的变化,那么系统的输出对这个输入的灵敏度就高。根据这个定义,局部灵敏度可以表示为系统输出在某个基准点对某个系统输入的一阶偏导数/导数/梯度:系统在这个基准点上对某个输入的一阶偏导数的值越大,那么在这个基准点上系统的输出对这个输入的灵敏度就高。
全局灵敏度
全局灵敏度用于衡量若干个系统输入整体的、大范围的变化对系统输出造成的影响。
局部灵敏度的计算方法
假设系统的微分方程表示为: \[\frac{dy_i}{dt}=f_i(y_i,p,t)\] 其中\(p\)为某个系统参数。
根据定义,某个系统输出\(y_i\)对\(p\)的局部灵敏度\(S_i\)是计算其对\(p\)的一阶偏微分:
\[S_i=\frac{∂y_i}{∂p}\]
近似微分法
根据数学中对导数和偏导数的定义,有: \[S_i=\frac{∂y_i}{∂p}=\lim_{Δp→0}\frac{y_i(p+Δp)-y_i(p)}{Δp}\] 当\(Δp\)非常小时(比如\(Δp=1‰p\)),该式子可以近似为:
\[S_i=\frac{∂y_i}{∂p}≈\frac{y_i(p+Δp)-y_i(p)}{Δp}\] 这样近似的好处是将偏导或者极限转化为了减法,计算量相比于原本的定义式要小不少,但是\(Δp\)的选取对灵敏度分析至关重要。
直接微分法
直接微分法(direct differential method)考虑了灵敏度随着时间变化,这个变化率可以写作灵敏度对于时间的偏导数:
\[\frac{∂S_i}{∂t}=\frac{∂}{∂t}(\frac{∂y_i}{∂p})=\frac{∂f(y_i,p,t)}{∂p}\] 根据链式法则,有: \[\frac{∂S_i}{∂t}=\frac{∂f_i}{∂p}+\sum_{j=1}^n\frac{∂f_i}{∂y_j}×\frac{∂y_j}{∂p}=\frac{∂f_i}{∂p}+\sum_{j=1}^n\frac{∂f_i}{∂y_j}×S_i\] 将上式矩阵化,有:
\[\bf{\dot{S}}=\begin{bmatrix}\frac{∂S_1}{∂t}\\\frac{∂S_2}{∂t}\\...\\\frac{∂S_n}{∂t}\\\end{bmatrix}=\begin{bmatrix}\frac{∂f_1}{∂t}\\\frac{∂f_2}{∂t}\\...\\\frac{∂f_n}{∂t}\\\end{bmatrix}+\begin{bmatrix}\frac{∂f_1}{∂y_1}&\frac{∂f_1}{∂y_2}&...&\frac{∂f_1}{∂y_n}\\\frac{∂f_2}{∂y_1}&\frac{∂f_2}{∂y_2}&...&\frac{∂f_2}{∂y_n}\\...&...&...&...\\\frac{∂f_n}{∂y_1}&\frac{∂f_n}{∂y_2}&...&\frac{∂f_n}{∂y_n}\\\end{bmatrix}×\begin{bmatrix}
S_1\\S_2\\...\\S_n
\end{bmatrix}\] \[\bf{\dot{S}}=\bf{f_p}+\bf{J×S}\] 直接计算法的优点是避免了\(Δp\)的选取的问题,但是对于复杂的问题需要耗时更久,计算量也更大。
除了上述两种方法外,还有伴随灵敏度方法(adjoint sensitivity method,应用格林函数对直接微分法的计算量进行简化。)和代谢控制分析方法(metabolic control anlysis,MCA,一种主要应用于生物建模的方法,通过公式计算每个输入和输出的灵敏度:\(C_x^y=\frac{x}{y}×\frac{∂y}{∂x}\))。
全局灵敏度的计算方法
全局灵敏度分析适用于输入振荡范围较大的场合。全局灵敏度分析通常会使用采样来模拟整个输入的变化情况,常用的采样方法是拉丁超立方采样。
拉丁超立方采样
拉丁超立方采样(Latin hypercube sampling)是一种采样方法,它可以保证在每个区间都拥有均等的采样次数。
具体而言,对于\(N\)个变量\(x_1,...,x_n\),拉丁超立方采样的过程是:
- 每个变量的值域均等地划分为\(M\)个区间。
- 对于每个区间,从其中随机地选择一个值,选择过程的概率服从该区间的概率密度函数。
- 将每个变量采样到的\(M\)个采样值组合,构成\(M×N\)维的采样结果。
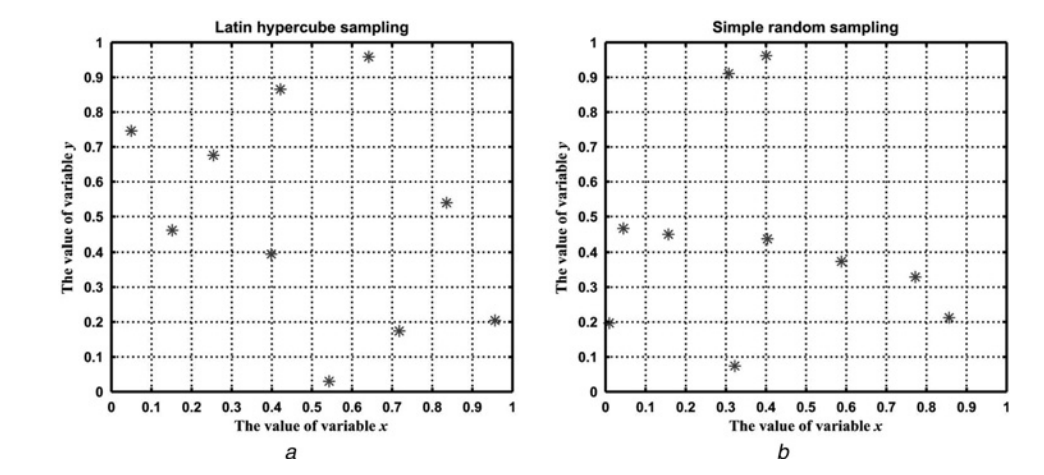
上图对比了拉丁超立方采样(a)和随机采样(b)的采样结果。可以发现,拉丁超立方采样在每个区间内都各有一次采样,保证了采样的公平性。而随机采样无法保证每个区间内被采样的次数都相同。
拉丁超立方采样的缺点是在抽样过程中实施了对样本方差的有偏估计,因此在使用基于方差的灵敏度方法时,应当避免使用拉丁超立方采样。
莫里斯灵敏度分析法
莫里斯灵敏度分析法(Morris sensitivity)的基本实现基于控制变量,即一次只改变一个变量。对于\(k\)个系统的参数/输入,其对每一个参数离散地采样\(p\)次,采样方法可以是蒙特卡罗方法,最终形成\(k×p\)的矩阵。对于第\(i\)个系统参数\(x_i\)的某次采样,其对整个系统影响的贡献(elementary effects)可以表示为:
\[d(x_i)=\frac{y(x_1,...,x_{i-1},x_i+Δ,x_{i+1},...,x_k)-y(x)}{Δ}\] 其中\(x∈[x_1,x_2,x_{k-1},x_k]\),是一个参考值。\(Δ=z\frac{1}{p-1},z∈z^*\)。
在莫里斯灵敏度分析中,\(r\)个输入变量的均值(\(μ=\frac{1}{r}\sum_{i=1}^rd_i\))和均方差(\(\sigma=\sqrt{\sum_{i=1}^r(d_i-μ_i)/q}\))称为这\(r\)个输入变量\(\bf{x_r}=[x_1,...,x_r]\)整体的灵敏度因子,可对\(\bf{x_r}\)的灵敏度进行判断:当平均值很小时,则说明\(\bf{x_r}\)对模型的影响很小,该参数不重要;当平均值较大,则说明\(\bf{x_r}\)与模型输出有线性关系;均方差比较小时,则说明该参数与其他参数的相关性弱;但当平均值和均方差都比较大时,则说明该参数与模型输出有非线性关系,并且该参数与其他参数的相关性、关联性强。
莫里斯方法的计算量比较小,但是只能在模型是单调的、且\(d(x_i)\)每次采样值均大于0时(避免采样之间相互对消而造成的干扰)效果才比较好。此外,\(p\)和\(Δ\)的选取也会对灵敏度分析产生影响。
系统的单调性:给定控制系统初始值的上下界,给定输入(也可理解为扰动)的上下界,以及控制模型,则可以得到控制系统状态的上下界。
WALS算法/有权局部灵敏度均值法
WALS算法(weighted average of local sensitivities)的想法和莫里斯方法相似,都是独立的对参数的灵敏度贡献进行计算,WALS算法的过程如下:
- 在整个参数空间中,随机地选取参数设置点,在计算该点下的每个参数的局部灵敏度。
- 按照玻尔兹曼分布:\(exp(-E/Tk_b)\)为每个参数赋予权重,其中\(E\)是该参数\(p\)下\(y(p+\Delta)\)该参数点一个参考输出\(y(p_r)\)的有权最小均方差(WLSE),\(y(p_r)\)可以通过实验进行观测;\(k_bT\)是一个尺度系数。具体而言,在参数空间中点\(\bf{x_k}\)下,参数\(p\)的有权局部灵敏度为:
\[w_p^k=exp\left(-\frac{WLSE(x_k)}{min[WLSE(x_i),i=1,2,...,N]}\right)\] 其中\(N\)表示在参数空间中的采样次数。
- 计算参数\(p\)的全局灵敏度:
\[WALS_p=\sum_{k=1}^NS_p^kw_p^k\] 其中\(S_p^k\)是参数\(p\)在点\(\bf{x_k}\)下的局部灵敏度。
WALS算法依赖于采样方法,由于存在均方差计算,其计算量相比莫里斯方法更大。
索伯灵敏度分析法
前两种灵敏度分析方法都基于采样,索伯灵敏度分析法(sobel sensitivity analysis method)基于方差,索伯方法是一种无偏的分析方法,在实施前没有假设模型的输入和输出有必然联系。索伯方法基于对系统输出的方差函数的分解:将关于系统输出的方差函数\(f(x)\)分解为多个输入变量导致的方差函数,并在这个过程中增加函数的维度。
对于整个输出函数\(f(x)\),可以分解为多个输入变量导致的输出:
\[f(x)=f_0+∑_{i=1}^kf_i(x_i)+∑_{i=1}^k∑_{j=i+1}^kf_{ij}(x_i,x_j)+...+f_{1...k}(x_1,x_2,...,x_k)\] 所有子项\(f\)都两两正交。
其中,输出函数的方差为:
\[D=∫f^2(x)dx-(∫f(x)dx)^2\]
某些输出变量导致的部分方差表示为:
\[D_{i_1,i_2,i_3,...,i_k}=∫...∫f^2(x_{i_1},...,x_{i_k})dx_{i_1}...dx_{i_s}\] 将\(f(x)\)平方后积分,可以发现总方差\(D\)和各阶方差和之间的关系:
\[D=\sum_{i=1}^kD_i+∑_{i=1}^k∑_{j=i+1}^kD_{i,j}+...+D_{1,2,...,k}\] 那么\(i_1,i_2,i_3,...,i_k\)整体的全局灵敏度可以表示为:
\[S_{i_1,i_2,i_3,...,i_k}=\frac{D_{i_1,i_2,i_3,...,i_k}}{D}\] 其中第\(i\)个输入的灵敏度表示为\(S_i=D_i/D\).
这里称\(S_i\)为变量\(x_i\)的一阶灵敏度系数,表示\(x_i\)对输出的主要影响。\(S_{i,j},i≠j\)表示二阶灵敏度系数,表示两个变量\(x_i,x_j\)之间的交叉影响。因此,\(S_{1,2,3,...,k}\)表示\(k\)阶灵敏度,表示\(k\)个变量\(x_1,..,x_k\)之间的交叉影响。
基于蒙特卡罗方法的索伯方法
索伯方法中的一个重要的问题是如何求解\(D_{i_1,i_2,i_3,...,i_k}\)。对此,索伯方法中指出对\(D\)包含的高阶积分可以通过蒙特卡洛方法求出:
\[\hat{f_0}=\frac{1}{n}\sum_{m=1}^nf(x_m)\] \[\hat{D}=\frac{1}{n}\sum_{m=1}^nf^2(x_m)-\hat{f}^2_0\] \[\hat{D_i}=\frac{1}{n}\sum_{m=1}^nf(x^{(1)}_{im},x^{(1)}_{(-i)m})f(x^{(1)}_{im},x^{(2)}_{(-i)m})-\hat{f}^2_0\] \[\hat{D_{-i}}=\frac{1}{n}\sum_{m=1}^nf(x^{(1)}_{(-i)m},x^{(1)}_{ik})f(x^{(1)}_{(-i)m},x^{(2)}_{ik})-\hat{f}^2_0\] \[\hat{D_{ij}^c}=\frac{1}{n}\sum_{m=1}^nf(x^{(1)}_{ijm},x^{(1)}_{(-ij)m})f(x^{(1)}_{ijm},x^{(2)}_{(-ij)m})-\hat{f}^2_0\] \[\hat{D_{ij}}=\hat{D_{ij}^c}-\hat{D_i}-\hat{D_j}\] 其中, \(n\)为抽样次数,\(x_{-i}\)表示去除\(x_i\)后其他的输入变量,\(x_{-ij}\)表示去除\(x_i\)和\(x_j\)后其他的输入变量,上标\((1)\)、\((2)\)为输入变量组 \((x_1.,x_2,...,x_k)\)的两个\(n × k\)维抽样数组,实质上就是对除\(x_i\)外其他参数分别进行两次抽样,而参数\(x_i\)仅抽样一次,再将两组抽样值分别代入模型进行计算,确定对应的方差。
因此,参数\(x_i\)的总灵敏度表示为:
\[\hat{S}_T(i)=1-\frac{\hat{D_{-i}}}{\hat{D}}\]
不难看出,索伯方法是一种计算量极大的算法。而且基于蒙特卡洛方法的索伯方法需要大量的样本数据来近似计算各种方差,通常需要成千上万次的采样。
傅里叶振幅分析法
另一种基于方差的全局灵敏度计算方法是傅里叶振幅分析法(FAST,Fourier amplitude sensitivity test)。傅里叶振幅分析法预先假设了所有的参数都与其他参数独立无关。傅里叶振幅分析方法的步骤是:
对每一个参数进行采样,第\(i\)个参数\(p_i\)的采样服从传递函数:
\[p_i=p_i^0e^{G_i(sinω_is)}\] 其中\(p_i^0\)是对\(p_i\)的一个参考值;\(G_i\)是\(p_i\)的概率密度函数在\(s\)域的表达;\(ω_i\)是一系列线性无关的整数角频率;\(s\)是一个尺度系数。 输出的期望为:\(\frac{1}{2π}\int_{-π}^πf(s)ds\),其中\(f(s)=f(G_1sin(ω_1s),...,G_ksin(ω_ks))\),根据帕塞瓦尔定律,有输出的方差为:
\[D≊2∑_{i=1}(A_j^2+B_j^2)\] \[A_j=\frac{1}{2π}\int_{-π}^πf(s)cos(js)ds\] \[B_j=\frac{1}{2π}\int_{-π}^πf(s)sin(js)ds\] 在这种方法下某个输入\(x_i\)的部分方差可以表示为:
\[D_i≊2∑_{p=1}(A^2_{pω_i}+B^2_{pω_i})\] \(p\)表示对\(x_i\)一共进行了\(p\)次采样。
那么,\(x_i\)的灵敏度可以表示为归一化方差:
\[S_i=\frac{D_i}{D}≊\frac{2∑_{p=1}(A^2_{pω_i}+B^2_{pω_i})}{2∑_{p=1}(A^2_{j}+B^2_{j})}\] 傅里叶振幅分析也是一种计算量非常大的方法。
评价
局部灵敏度和全局灵敏度
从整个系统的参数空间(即整个系统所有可能的参数设置的范围)上来看,局部灵敏度只能在一个基准的参数设置点上衡量小范围变化的影响程度,因此灵敏度的可靠性依赖于这个基准点的参数设置。此外,相比于全局灵敏度,单个或者几个一阶导的计算使得局部灵敏度的计算量要远远小于全局灵敏度。
而全局灵敏度不需要依赖某个点的参数设置,它更适用于输入变量在较大范围内变化的情况。
全局灵敏度分析法的选择
全局灵敏度分析法可以分为三种:基于采样的分析方法(WALS法)、基于筛选的方法(莫里斯方法)和基于方差的分析方法(索伯分析、傅里叶振幅分析)。
基于方差的分析方法计算量非常大;而对于基于筛选的莫里斯法,在输入变量数量较多的情况下,采样次数较多,计算所有输入变量的方差和均值的计算量也比较大,此外在系统模型非单调的前提下,在计算均值时,不同输入变量之间的灵敏度贡献可能被相互抵消掉;而基于采样的WALS方法所需要的计算量相比于前两者更小。莫里斯法和许多基于采样的灵敏度分析法都基于系统是单调的假设,在系统是非单调的条件下,一般采用基于方差的灵敏度分析方法。
灵敏度分析的局限性
灵敏度分析为系统建模提供了变量之间关系的衡量,但是灵敏度没有直接描述这样的关系或者机制。变量本身的描述方式决定了灵敏度分析的准确性,当变量本身描述较差时,灵敏度分析结果也可能不能完全反映变量之间的关系,因此,应当在灵敏度分析之后,使用实验(比如控制变量、施加微小干扰)对变量之间的关系进行验证。