1.2. 梯度下降算法

梯度下降算法

在开始之前规定几个符号所代表的意义：
\(m\) 训练集中训练样本的数量
\(X\) 输入变量
\(Y\) 输出变量
\((x,y)\) 训练样本
\((x^i,y^i)\)第i个训练样本（i表示一个索引）
## 监督学习算法的流程 提供训练集>学习算法得到\(h\)（假设函数：用于描绘\(x\)与\(y\)的关系）>预测\(y\) 的值

假设函数

假设函数(Hypothesis function)——\(h\)是用来表示某一个数据集可能存在的线性/非线性关系的函数。对于线性拟合，其假设函数为：
\[h_θ(x)=θ_1x+θ_0\] 其中\(θ\)是假设函数当中的参数。 如果不考虑截距项\(θ_0\)，\(h_θ(x)\)可以简化为： \[h_θ(x)=θ_1x\]

代价/损失函数

代价函数（Cost/Loss function），在统计学上称为均方差误差函数(Mean Square Error, MSE)，其用于衡量模型预测结果和真实结果之间的差值：当假设函数中的系数\(θ\)取不同的值时，\(\frac{1}{2m}\)倍假设函数预测值\(h_θ(x^{(i)})\)和真实值\(y^{(i)}\)的差的平方的和之间的函数关系表示为代价函数\(J\)。 \[J(θ_0,θ_1)= \frac{1}{2m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})^2 \] > 取1/2的原因是便于消除求导之后产生的2倍,同时也可以进一步缩小\(θ\)

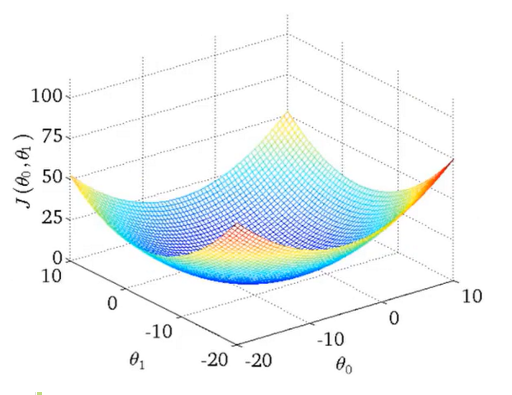
线性回归的代价函数的自变量有两个：\(θ_1\)和\(θ_0\)，因此该函数是三维的函数。线性回归的代价函数图像如下图所示：

代价函数在几何上表示为数据集空间内的各点到假设函数的欧式距离的平方的平均值的一半。
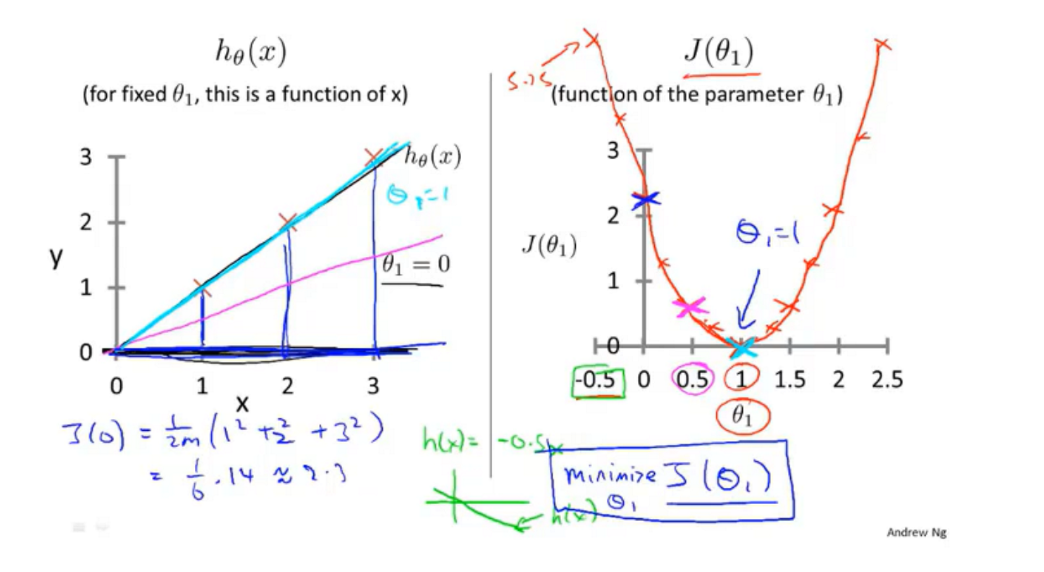
要想使得数据能够被假设函数很好地拟合，那么代价函数要尽量地小。当代价函数取到它的最小值即\(J(θ_1)_{min}\)时，此时的填入假设函数的\(θ\)对数据的拟合程度是最好的。
对于线性的代价函数，假设函数对数据集的拟合程度越高，对应的\((θ_0,θ_1)\)越接近代价函数图像等高线的中心。

## 梯度下降算法（Gradient Descent）
### 梯度 在微积分中，函数\(f(x,y)\)在\((x_0,y_0)\)处是函数值增加最快的方向是梯度(Gradient) 的方向，梯度的反方向是函数值减小最快的方向。
由微分知识可以知道，\(f(x,y)\)在\((x_0,y_0)\)处的梯度表示为：
\[▿f|_{(x_0,y_0)}=(\frac{∂}{∂x}f(x_0,y_0),\frac{∂}{∂y}f(x_0,y_0))\]

概述

梯度下降算法是一种求解代价函数最小值的方法，它可以用在多维任意的假设函数当中。
简而言之，梯度下降算法求得\(J(θ_1)_{min}\)的主要思路是：
1. 给定\(θ_0\)和\(θ_1\)的初始值，通常令\(θ_0=0\)，\(θ_1=0\)。 2. 不断改变\(θ_0\)和\(θ_1\)的值使得\(J(θ_0,θ_1)\)的值逐渐变小，直到找到\(J(θ_0,θ_1)\)的最小值或者局部最小值。
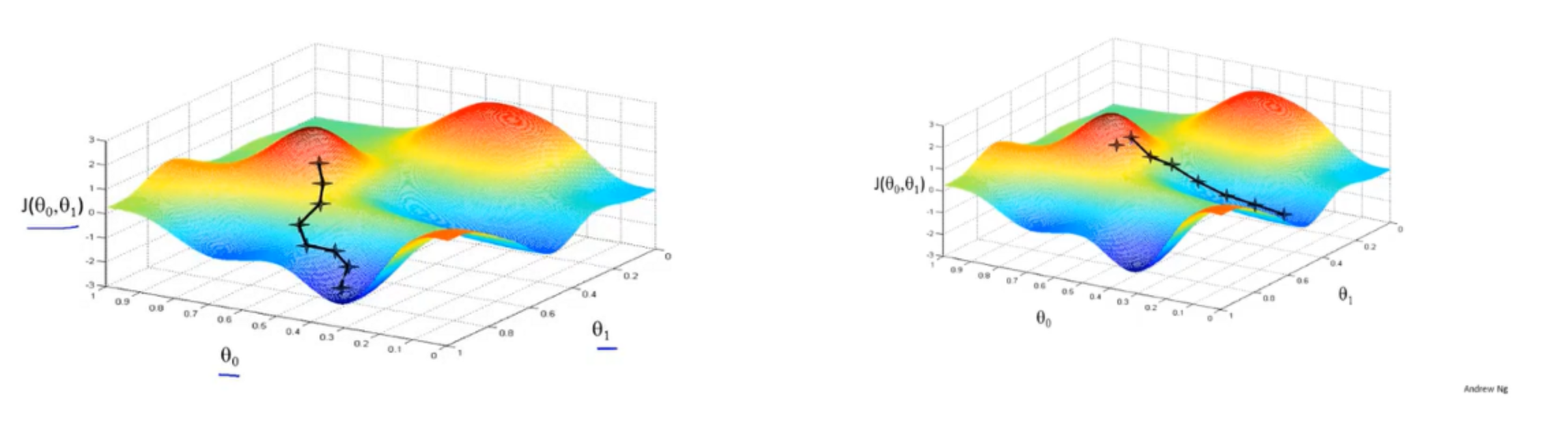
如果从一个初始值出发，寻找附近的最小值，重复该过程，得到上图，最后得到的值为局部最优解。
> 将梯度下降算法类比为爬山，从一个点开始，不断寻找“下山”的路线，最后找到一个“下山”的出口。

当改变初始值时，会找到另一条“下山”的路径，找到第二个局部最优解（局部最小值）。

对于线性回归的代价函数而言，只存在一个局部最小值。（见线性回归代价函数的图像）
### 表示
梯度下降算法可以表示为：

Algorithm
Repeat untill convergence:{  \(θ_j:=θ_j-α\frac{∂J(θ_0,θ_1)}{∂θ_j},j=0~and~j=1\) }

解释：
1. \(:=\) 表示赋值运算符 2. \(α\)称为学习率，用来控制下降的步长（Padding），即更新的幅度：
- \(α\)太小，同步更新的速率会非常的慢。
- \(α\)过大，同步更新时可能会越过最小值点，导致拟合效果不好。
3. \(\frac{∂J(θ_0,θ_1)}{∂θ_j}\)是代价函数的梯度： \[\frac{∂J(θ_0,θ_1)}{∂θ_0}=\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})\] \[\frac{∂J(θ_0,θ_1)}{∂θ_1}=\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x^{(i)}\]

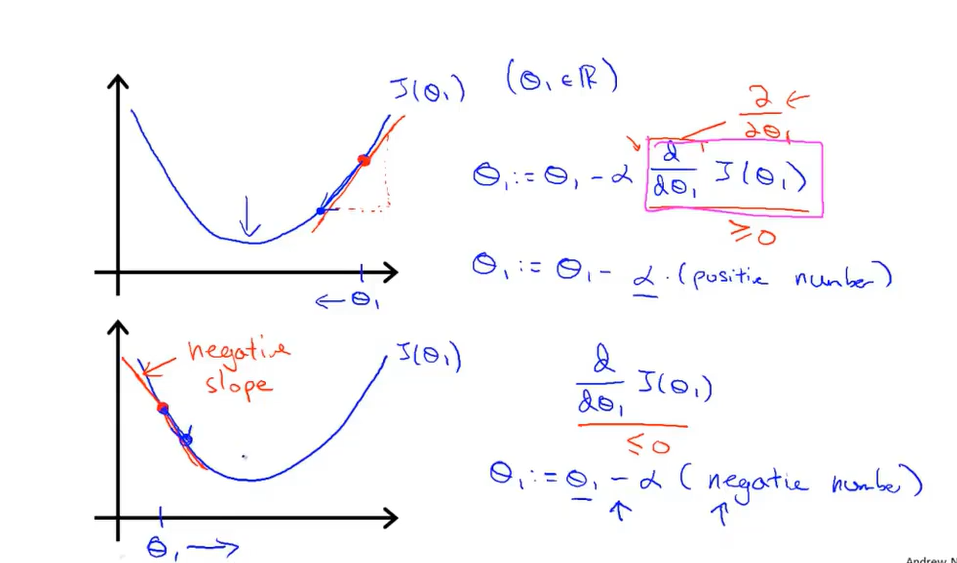
△在代价函数中（以简化的代价函数为例），无论初始值在最小值点的左侧还是右侧，通过同步更新都能够使该点被移动到最小值，在最小值点，由于导数值为0，最终同步更新停止在了\(θ_j=θ_j\)，此时的\(θ_j\)即为极小值点。

同步更新

同步更新（Simulaneous update）是梯度下降算法中用于处理多个参数\(θ\)的方式。

Algorithm
\(temp0:θ_0:=θ_0-α\frac{∂J(θ_0,θ_1)}{∂θ_0}\) \(temp1:θ_1:=θ_1-α\frac{∂J(θ_0,θ_1)}{∂θ_1}\) \(θ_0:=temp0\) \(θ_1:=temp1\)

这个更新方程能够同时更新\(θ_0\)和\(θ_1\)。
更新的方法是计算赋值号右边带入\(θ_1\)和\(θ_2\)的值进行计算，得到的两个值分别储存在temp0和temp1中，从上到下进行赋值。

对于简化的代价函数：
\[θ_1：=θ_1-αJ'(θ_1)\]
\[\frac{dJ(θ_1)}{dθ_1} =\frac{d}{dθ_1}(\frac{1}{2m}Σ(h_θ(x_i)-y_i))^2)\]

将梯度代回代价函数中就得到了批量梯度下降算法的基本形式：
重复如下的更新方程，直到\(θ_0\)和\(θ_1\)都收敛 \[θ_0:=θ_0-α\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})\] \[θ_1:=θ_1-α\frac{1}{m}∑_{i=1}^m(h_θ(x^{(i)})-y^{(i)})x^{(i)}\]

本节学习的梯度下降算法在每一轮迭代时都要对数据集中所有的数据进行求和，因此称为批量梯度下降算法。这种算法在数据集的数据量非常大时，执行算法所消耗的计算量相当大。因此在大数据集学习时，采用另一种梯度下降的方式，称为随机梯度下降。
关于随机梯度下降的的内容：13.2. 随机梯度下降算法