常考知识点

本文最后更新于 2023年10月20日 上午

电路与器件常考知识点

针对Brunel University 2020: EE1618 Devices and Circuits的期末复习笔记
Lecturer: Dr. Ruiheng Wu（武瑞恒）/Dr. Chunsing Lai（赖俊升）
图因为挂在了github上，需要通过科技才能够看得到。

电学部分知识点

静态电路分析

1. Y- \(\Delta\) 形电路转换

现推方法：
从Y电路的两个节点看整个电路，必然只有两个电阻被串联使用
从\(\Delta\) 电路的两个节点看整个电路，电路呈现一个电阻与两个串联电阻并联的情况
列出两个电路的方程，求解即可
公式：
\[ R_3=\frac{R_a R_b}{R_A+R_B+R_C} \] > 注：\(R_3\)是Y- \(\Delta\) 形电路中属于Y的，且在\(\Delta\)电路中 \(R_a\)与\(R_b\)中间的电阻

当\(R_A=R_B=R_C\)时，
\[ R_Y=\frac{R_Δ}{3}\]

2. 最大功率传输定理

最大功率传输定理针对的是某一部分的最大功率
当负载\(R_L\)的电阻值与内电路电阻值相等时，有负载的功率最大
结合戴维南定理，可以将\(R_L\)外的所有部分等效为一个内电路，当 \(R_L=R_{Th}\) 时有\(R_L\)的功率最大。

动态电路元件

1. 电容

  • 连接方式
    串联： \[ \frac{1}{C_t}=\frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_n} \] 并联： \[ C_t=C_1+C_2+...+C_n\]

  • 动态响应方程
    时间常数：
    \[ \tau = RC \]
    未充电： 断路
    充电阶段： \[ v_C(t)=E(1-e^{-\frac{t}{τ}})\] \[ i_C(t)=\frac{E}{R}e^{-\frac{t}{τ}}\] 充电完成：短路（理想）
    开关断开的瞬间: \[ u(0_+)=u(0_-)\] 放电阶段：
    \[ v_C(t)=Ee^{-\frac{t}{τ}}\] \[ i_C=\frac{E}{R}e^{-\frac{t}{τ}}\] 放电完成： 断路

  • 交流电路响应
    阻抗：
    \[ Z_c=X_c=-\frac{1}{ωC}j=\frac{V_m}{I_m}\] >j是虚数单位

    随着频率的增加，阻抗会逐渐减小

2. 电感

  • 电感的定义 \[L=\frac{Φ}{I}\]

  • 连接方式
    串联： \[L_t=L_1+L_2+...+L_n \] 并联： \[ \frac{1}{L_t}=\frac{1}{L_1}+\frac{1}{L_2}+...+\frac{1}{L_n} \]

  • 动态响应方程
    时间常数：
    \[ \tau = \frac{L}{R} \]
    未充电： 短路
    充电阶段： \[ v_L(t)=Ee^{-\frac{t}{τ}}\] \[ i_L(t)=\frac{E}{R}（1-e^{-\frac{t}{τ}}）\] 充电完成：断路（理想）
    开关断开的瞬间: \[ i(0_+)=i(0_-)\] 放电阶段：
    \[ v_L(t)=Ee^{-\frac{t}{τ}}\] \[ i_L=\frac{E}{R}e^{-\frac{t}{τ}}\] > 注：放电过程应当与L并联一个电阻以保护整个电路的安全，因此此处的R的阻值与原来相比已经发生了变化

    放电完成： 短路

  • 交流电路响应
    阻抗： \[ Z_L=X_L= ωL=\frac{V_m}{I_m}\] 随着频率的增加，阻抗会逐渐增加

  • 谐振
    当电路处于谐振状态时， 有： \(-X_c=X_L\)
    根据该公式可以求出谐振频率。
    在谐振电路中：\(I=\frac{E}{R}\)
    谐振的时候功率因子为1.
    品质因数（Q）： \[Q=\frac{Q(power)}{P}=\frac{X_L}{R}（串联）=\frac{R}{X_c}(并联)\]

交流电基础

  1. 复角表达
    以 \(v=V_msin(\omega t+ θ)\)为例： \[v=V_msin(\omega t+ θ) →V_{rms} ∠θ\] \[V_{rms}=\frac{V_m}{\sqrt{2}}\] \[V=V_{rms}=V_{rms} ∠θ\] > 相位角相同才能用复角表示

  2. RLC-交流电电路的功率
    平均功率/有功功率： \[ P=V_{rms}I_{rms}cos\theta=\frac{V_{m}I_{m}}{2}cos\theta\] >在不含LC的交流电电路中：\(P=V_{rms}I_{rms}=\frac{V_{m}I_{m}}{2}\)

    \[ P=I_{rms}^2R\] 功率因子： \[cos\theta=\frac{P}{S}\] 视在功率： \[S=V_{rms}I_{rms}\] \[S=I_{rms}^2Z\] 无功功率： \[Q=V_{rms}I_{rms}sin\theta\] \[Q=I_{rms}^2X\] \[Q=\sqrt{S^2-P^2}\] > 一般采用通过计算P和S的方式来计算Q

无源滤波器

  1. 增益
    功率增益： \[A_{p}=\frac{P_o}{P_i}\] 对数形式： \[A_{p}=10lg(\frac{P_o}{P_i})\] >10

    电压增益： \[A_{v}=\frac{V_o}{V_i}\] 对数形式： \[A_{v}=20lg(\frac{V_o}{V_i})\] >20

  2. 滤波器电路的连接和功能

    • 根据电容和电感频率响应的特性具体问题具体分析
    • 截止频率在\(X_L=R\)或者\(X_C=R\)时
    • 相位角：\(\theta=arctan(\frac{f_{cutoff}})\)
    • 在截止频率时，相位角为45°
    • 无源带通滤波器的结构是高通和低通滤波器并联

变压器

  1. 变压器的性质

    • 变压器可以变换阻抗，电压，电流
    • 变压器的耦合系数： \[ k=\frac{Φ_m}{Φ_p}\]
      >\(Φ_m\)：次级磁通量，\(Φ_p\)：初级磁通量

    初级电动势： \[ e_p=N_p \frac{d \Phi_p}{dt}=L_p\frac{d i_p}{dt}\] 次级电动势： \[ e_s=N_s \frac{d \Phi_m}{dt}=kN_s \frac{d \Phi_p}{dt}\]

  2. 互感系数（Mutual Inductance）
    \[M=N_s\frac{d \Phi_m}{di_p}=N_s \frac{d \Phi_p}{di_s}\] \[M=k\sqrt{L_p L_s}\] 有， \[ e_p=M\frac{di_p}{dt}  和  e_p=M\frac{di_s}{dt}\] >注意下标

  3. 比例关系
    \[a=\frac{N_p}{N_s}=\frac{e_p}{e_s}=\frac{i_s}{i_p}\]

电子元件部分知识点

半导体原理

  1. 半导体类型
    N型半导体： 填入电子
    P型半导体： 抽去原有的电子
  2. PN结及性质
    PN结： P型半导体和N型半导体拼接在一起，使得电流的方向仅能从P极到N极
    正向偏置： 电流由P到N，P-N结的电阻非常的小，可视为短路
    反向偏置： 电流由N到P，P-N结的电阻非常大，可视为断路

二极管电路

  1. 二极管的单向导通性
    对于理想二极管，顺箭头方向可视为导线，逆箭头方向可视为断路

  2. 二极管电路分析
    先假设二极管是导通的，求出二极管所在支路的电流方向，如果解出电流方向为逆箭头方向，则实际的二极管处于反向偏置状态，假设错误；如果解出的电流方向为顺箭头方向，则二极管处于正向偏置状态，假设正确，以此来判断电路中的二极管是否处于导通状态
    > 错误的假设情况下 需要重新计算电路

  3. 非理想二极管的等效模型
    非理想的二极管可以等效为一个理想的二极管和一个0.7V的直流电压源串联

  4. 二极管的应用

    • 半波整流器
      结构：交流电源和二极管串联
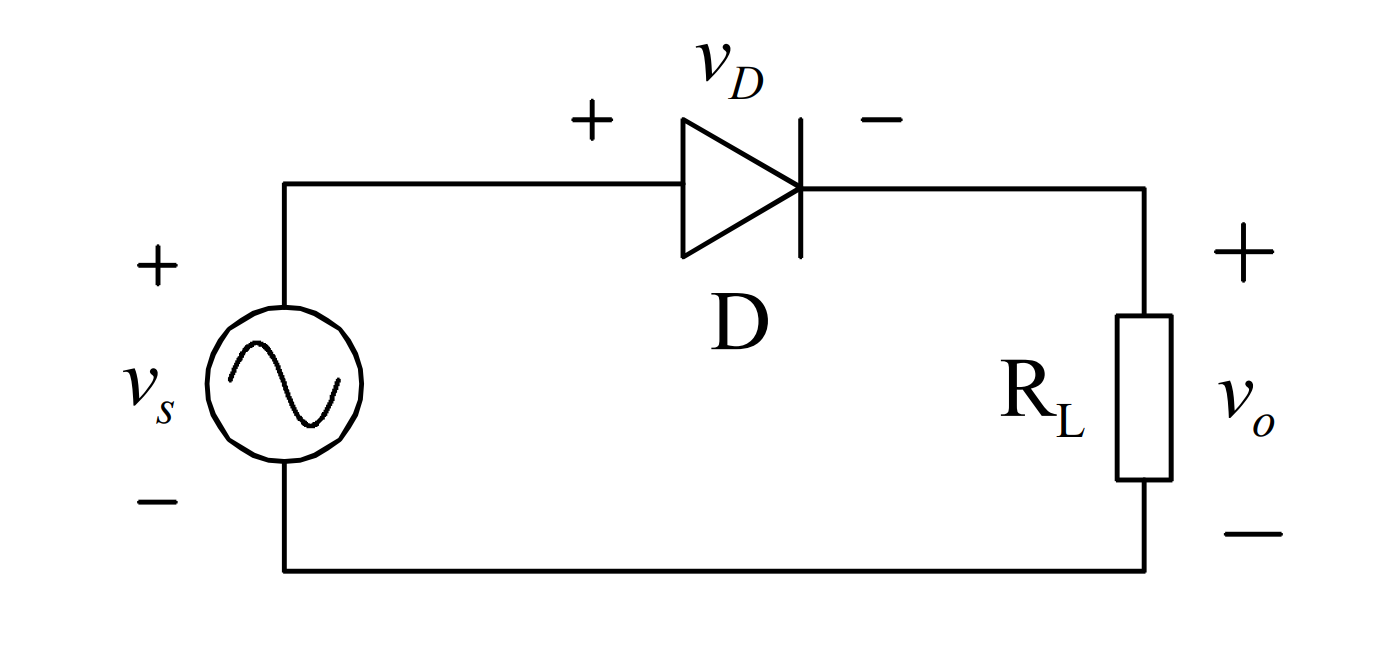
      分析：交流电源的某一方向可以通过二极管，达到整流器的作用

    • 全波/桥式整流器
      结构：
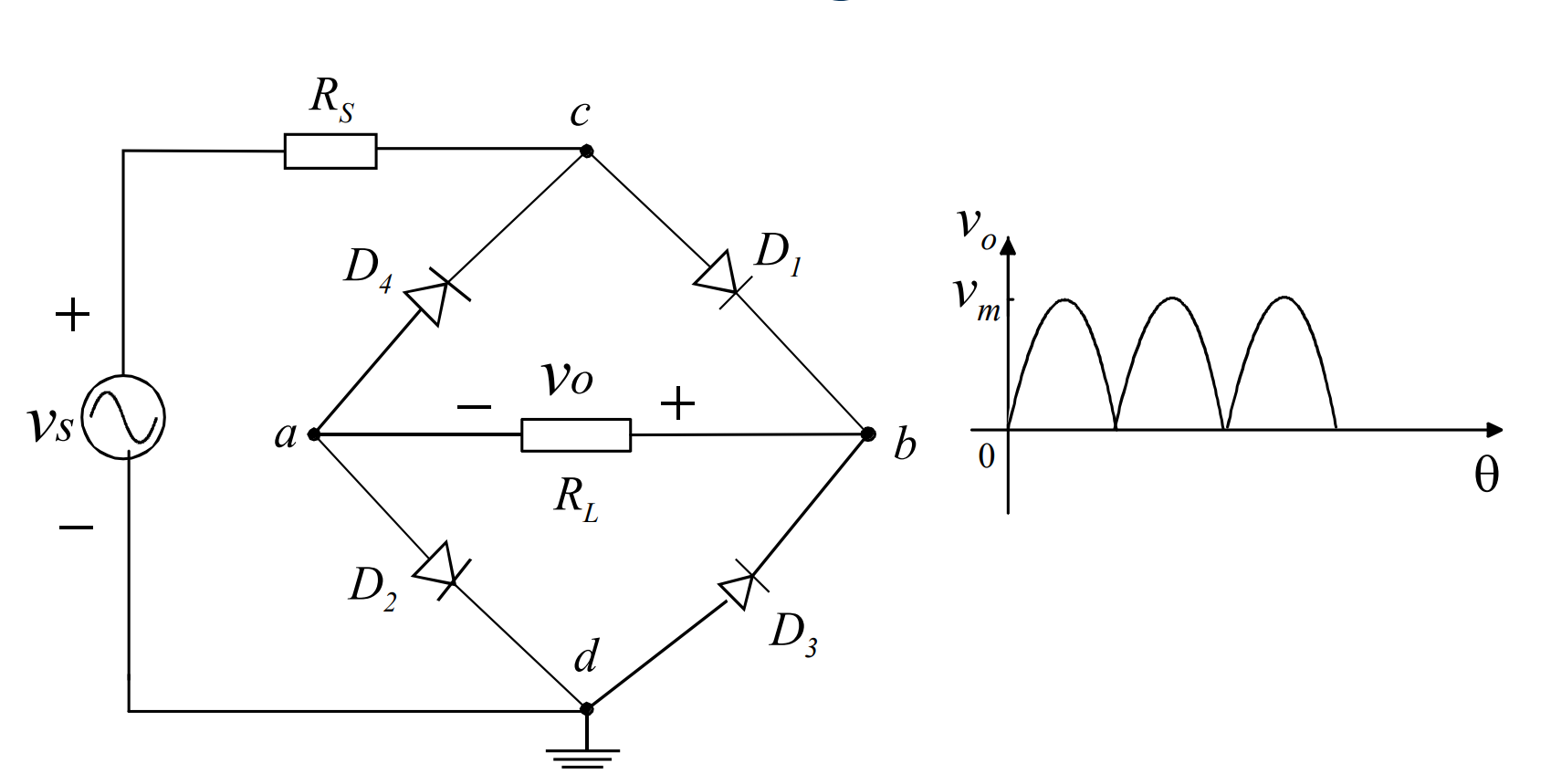
      分析： 无论是交流电源的前半期还是后半期，流过电阻的电流始终是同一个方向

    • 全波/变压器整流器
      结构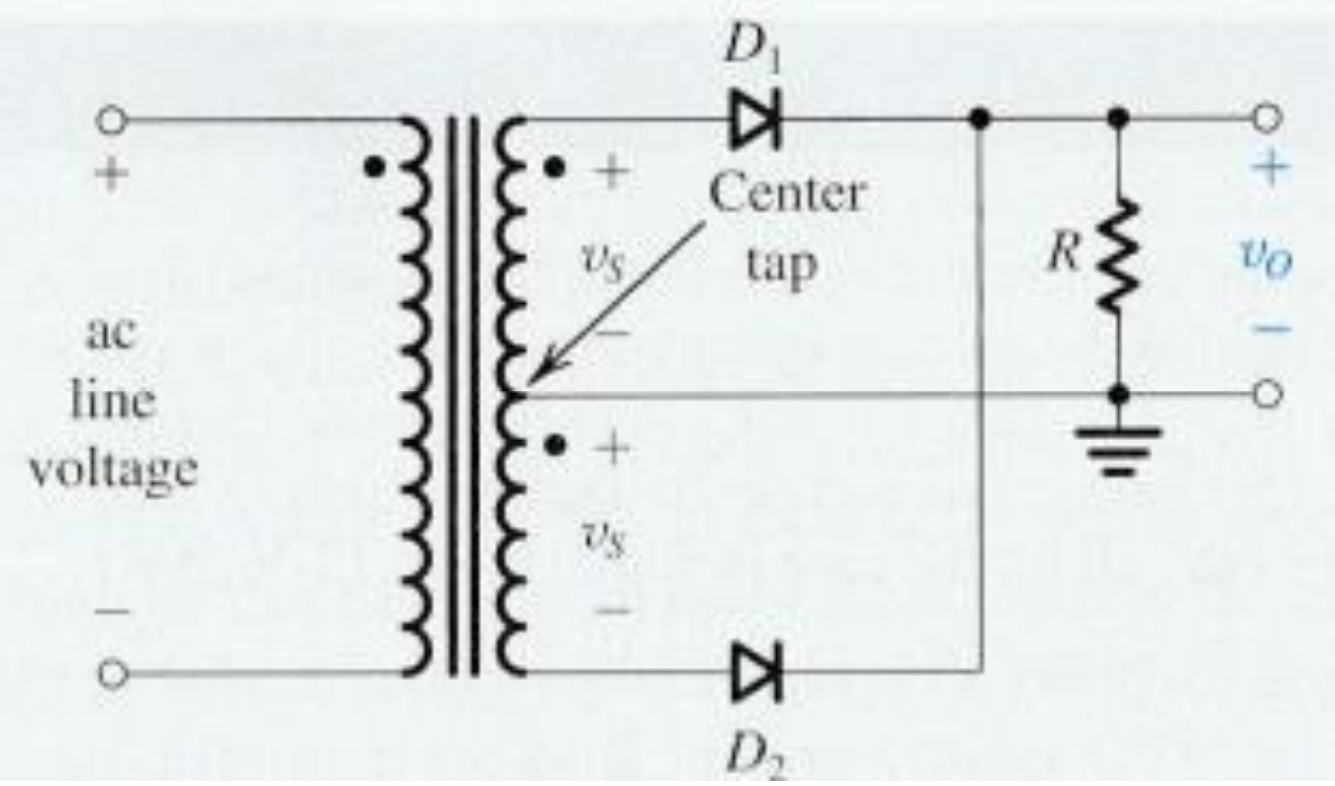： 分析： 变压器的输出端被分成了两段，在交流电的前半期还是后半期，电流都能通过其中的一半电路，流过电阻的电流是同一个方向 >由于引入了变压器，这种整流器的噪声非常的大

    • 并联限流器
      结构：二极管和直流电压源E串联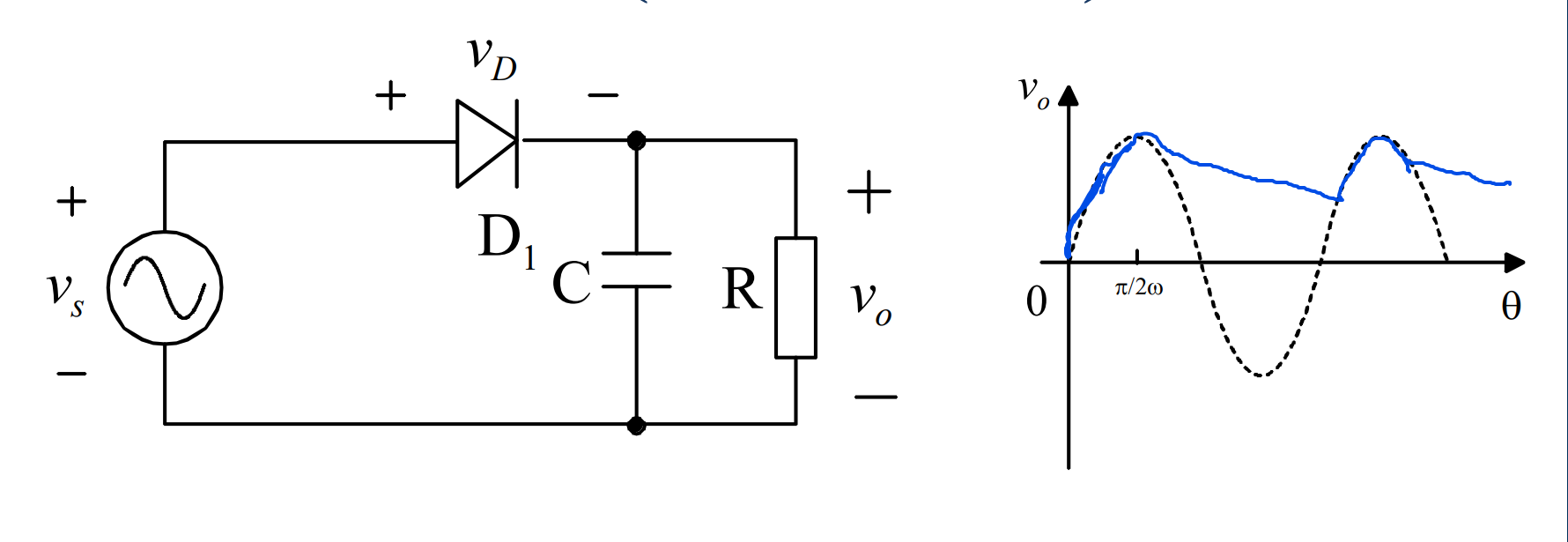 分析：当\(|V_{sin}|<E\)时，二极管导通\(V_{out}=E\)
      当\(|V_{sin}|>E\)时，二极管导通\(V_{out}=V_{sin}\)

    • 峰值限流器
      结构：二极管和（电容器||电阻）结构串联
      分析： 在交流电源的前半期，二极管导通，电容器断路，处于充电状态
      在交流电源的后半期，二极管断开，电容器放电维持电路的工作

运算放大器

  1. 放大器的增益
    线性增益： 输出与输入的比值是一个定值
    电压增益： \(A_v=\frac{V_o}{V_i}\)
    电流增益: \(A_i=\frac{I_o}{I_i}\)
    功率增益: \(A_P=\frac{P_o}{P_i}=A_vA_i\)
    增益的指数形式: \(A_p=10lg{\frac{P_o}{P_i}}\)
    > 10

    \(A_v=20lg{\frac{V_o}{V_i}}\)
    >20

    饱和状态： 对于有两个电源的运算放大器，输出电压不会超过最大/最小饱和电压

  2. 理想放大器的直流线性等效模型

    • 电压等效模型
      结构: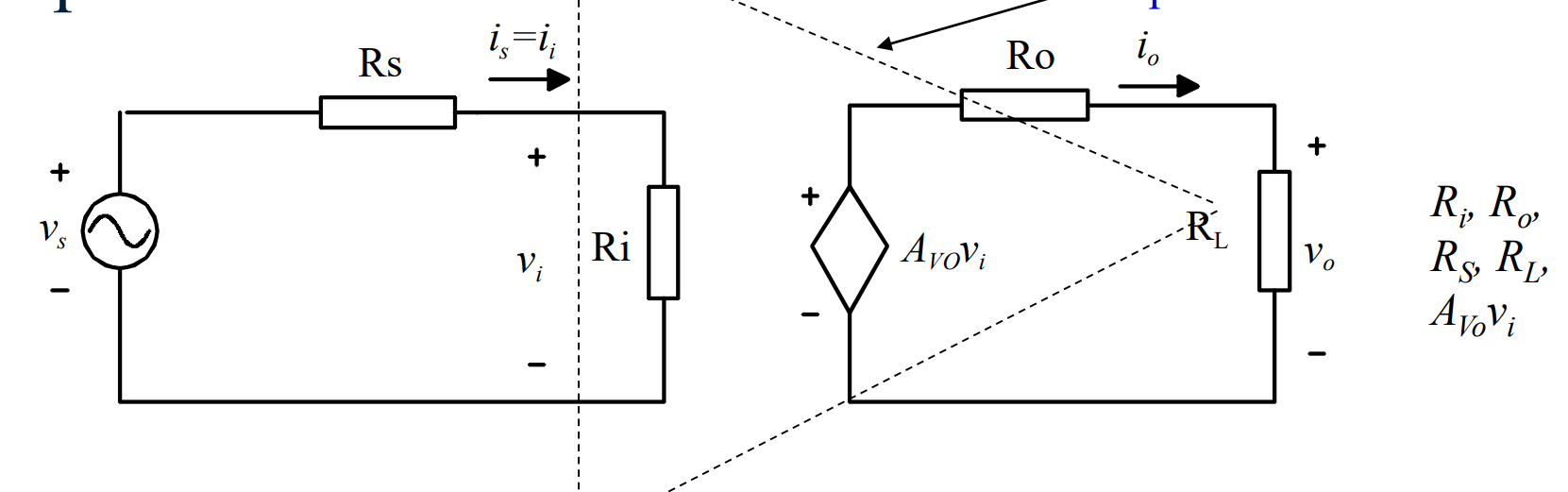
      分析： \[\frac{V_s}{V_i}=\frac{R_s+R_i}{R_i} \tag{1}\] \[\frac{A_{V_o}V_i}{V_o}=\frac{R_O+R_L}{R_L} \tag{2}\] \[A_v=\frac{V_o}{V_s}=\frac{V_o}{V_i}\frac{V_i}{V_s}=\frac{A_{V_o}}{(1+\frac{R_s}{R_i})(1+\frac{R_O}{R_L})}\]

      对于理想的运算放大器:
      \(A_o=∞,R_i=∞,R_o=0\)

    • 电流等效模型

  3. 级联放大器的增益计算

    • 一般形式： \[A_t=\Pi A_i\]
    • 指数形式： \[A_t =\Sigma A_i\]

  4. 运算放大器的符号和端口

    • pin1：反相输入端
    • pin2：同相输入端
    • pin3：输出端

  5. 运算放大器电路分析

    • 虚短路和虚接地
      在线性应用当中，电流从+ 流向 -时（同相输入）运算放大器的同相输入端和反相输入端之间可以认为是短路的，称为虚短路。
      当电流从-流向+时（反相输入），反相输入端相当于接地，称为虚接地。

    • 反相输入的运算法放大器电路分析
      电路图: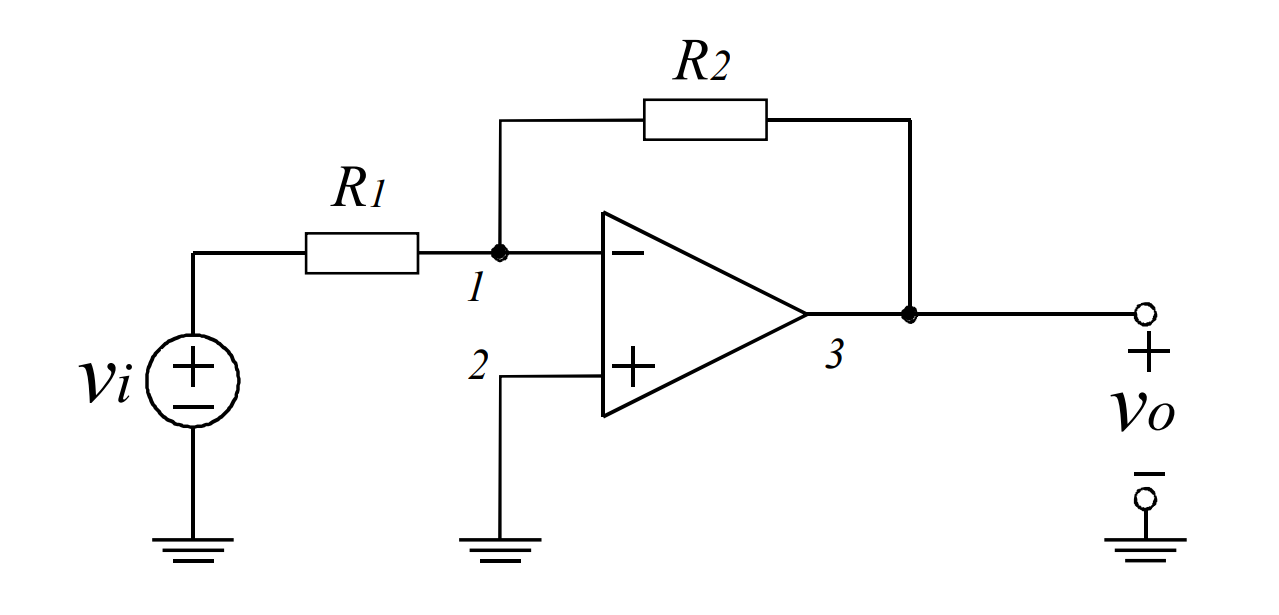 如图，
      由虚接地\(V_-=0\): \[i_1=\frac{V_i}{R_1}\] \[i_2=\frac{-V_o}{R_2}\] 同时，\(i_1=i_2\)
      电压增益：\(A_v=\frac{V_o}{V_i}=-\frac{R_2}{R_1}\)
      >反向放大器使用负反馈牺牲增益来增加精度

      反相加法放大器（2个输入电阻的情况）：
      \[i_1=\Sigma_{x=1}\frac{V_x}{R_x} \tag{1}\] \[i_2=\frac{-V_o}{R_f} \tag{2}\] \[i_1=i_2 \tag{3}\] \[V_o=-R_f \Sigma_{x=1}\frac{V_x}{R_x}\]

    • 同相输入的运算放大器电路分析
      电路图: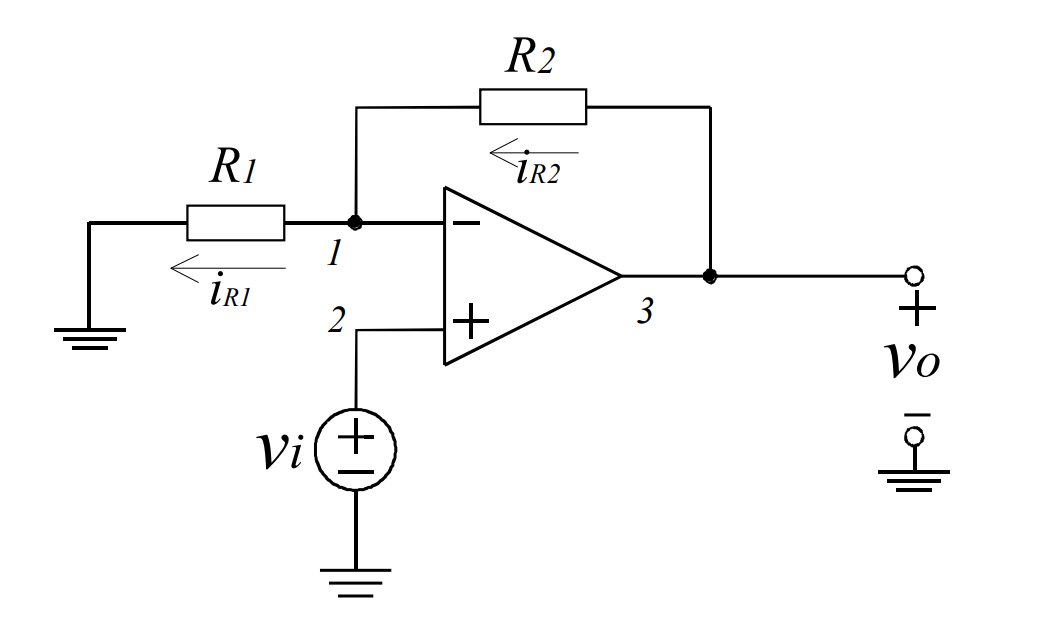
      如图， 由虚短路\(V_+=V_-=V_i\):
      \[i_1=\frac{0-V_i}{R_1}\] \[i_2=\frac{V_o-V_i}{R_2}\] 同时，\(i_1=i_2\)
      电压增益：\(A_v=\frac{V_o}{V_i}=1+\frac{R_2}{R_1}\)
      同相加法放大器（2个输入电阻的情况）：
      设输入节点电压为\(V_n\), 有： \[\frac{V_o}{V_n}=1+\frac{R_f}{R_b} \tag{1}\] 由叠加定理：
      \[V_n=\frac{R_2}{R_1+R_2}V_1+\frac{R_1}{R_1+R_2}V_2 \tag{2}\] \[V_o=(1+\frac{R_f}{R_b}) (\frac{R_2}{R_1+R_2}V_1+\frac{R_1}{R_1+R_2}V_2)\]

三极管电路

  1. 三极管电路的符号和三种模式
    • 三极管有PNP和NPN型两种，无论是哪一种，三极管的箭头永远是在基极（B）和发射极（E）两端，由P型半导体指向N型半导体(即激活态下三极管BE的电流方向)
    • 三种模式： 激活态（相当于放大器）、截止态、饱和态（CE之间短路）
  2. 激活状态下的电路分析
    • 电流关系
      \[i_E=i_B+i_c\] \[\frac{i_C}{i_B}=\beta\] >当\(β>100\)时，通常可以认为\(i_C=i_E\)
      \[V_{BE}=0.7V\] >\(V_B\)和\(V_E\)的孰大孰小由半导体类型决定

    善用戴维南等效定理，对复杂的三极管电路进行化简

    • KVL在直流三极管电路下的应用
      如果E最后未接地而接的电源，则可以对BE间进行KVL分析，列出方程，结合电流关系解出方程

反馈模型

  1. 反馈模型的结构
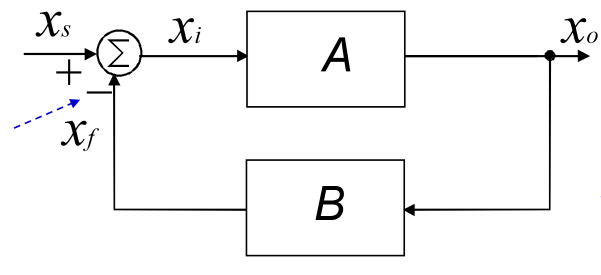
    开环增益：当电路中没有反馈结构B时候的输入与输出之比：\(A=\frac{x_o}{x_i}\)
  2. 反馈放大器的闭环增益
    \[A_f=\frac{x_o}{x_i}=\frac{A}{1+AB}\] 推导： \[x_o=Ax_i \tag{1}\] \[x_f=Bx_o \tag{2}\] \[x_s=x_f+x_i=x_i+ABx_i \tag{3}\] \[A_f=\frac{x_o}{x_i}=\frac{A}{1+AB}\]
  3. 反馈放大器的优点
    当\(AB\)足够大时，\(A_f=\frac{1}{B}\),
    反馈电路（B）通常是由无源器件（RLC）组成，因此此时的增益十分稳定而且可以直接精确地计算得出，即：
    • 准确
    • 可预测
    • 稳定

电闸管

  1. 肖克利二极管

    • 结构
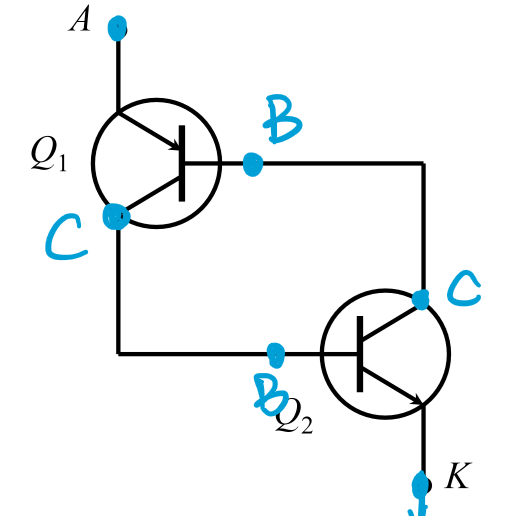
      两个PNP，NPN三极管串联，其中：
      \(B_1 →C_2\) 且 \(C_1 →B_2\)
      \(E_1=A,E_2=K\)

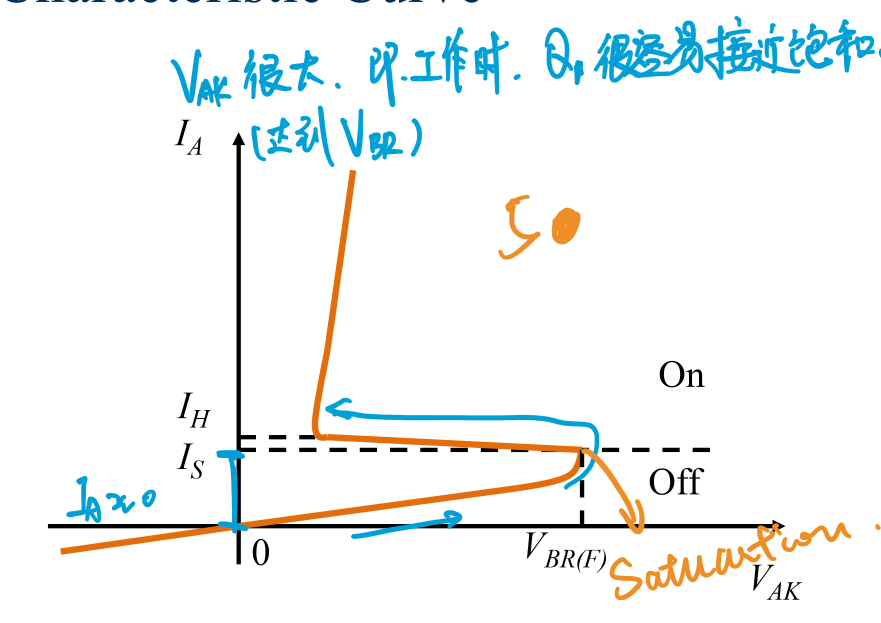
    • 特性曲线 当AK之间的电压非常小时,流过肖克利二极管的电流\(I_A\)非常小，即肖克利二极管表现大电阻的特性 当\(V_{AK}=V_{BR}\)时，A的三极管很容易饱和，此时会回落到某个电压，此后肖克利二极管可视为小电阻或者导线

  2. 锯齿波发生器
    • 结构
      肖克利二极管和电容器并联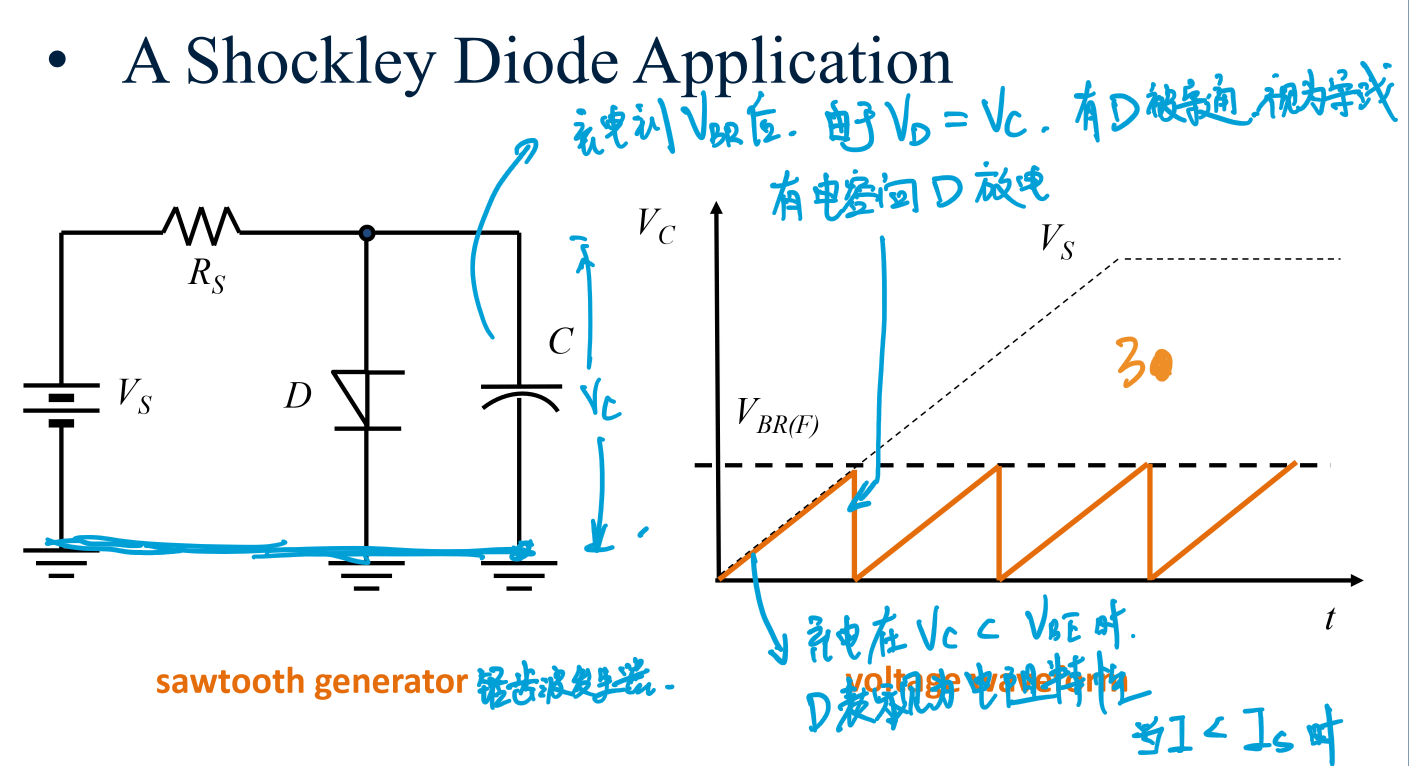
    • 分析
      肖克利二极管和电容器两端的电压相等，设为\(V_C\),
      当\(V_C<V_{BR}\)时，肖克利二极管表现大电阻特性，电容器充电
      当\(V_C>V_{BR}\)时，肖克利二极管表现小电阻特性（相当于短路），电容器迅速放电
  3. SCR整流器

    • 结构
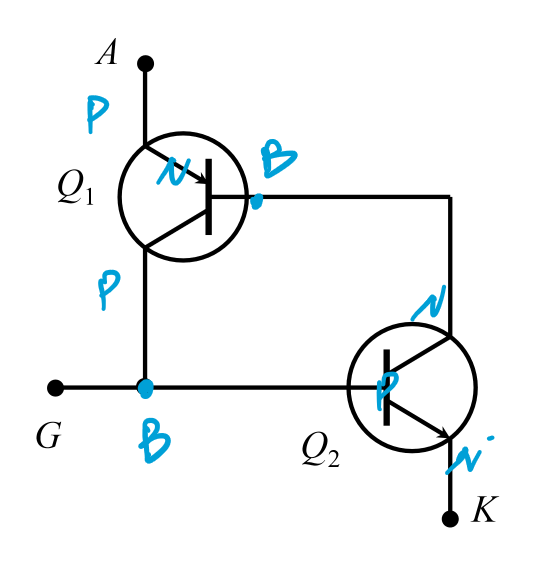
      两个三极管串联，其中：
      \(B_1 →C_2\) 且 \(C_1 →B_2\)
      \(E_1=A,E_2=K，B_2=G\)

    • 原理
      给\(B_2\)一个非常小的电流\(i_G\), \[i_{B2}=i_G\] \[i_{C2}=\beta_2 i_G=i_{B1}\] \[i_{C1}=\beta_1 i_{C2}=\beta_1 \beta_2 i_G=i_{B2}\] \[...\] 最终\(i_{B2}\)会非常大

    • IG0=0时的特性曲线
      同肖克利二极管

标准电源调节

  1. 线性调节公式 \[Line Regulation=\frac{\frac{\Delta V_{out}}{V_{out}}\times 100\%}{ΔV_{in}}\]
  2. 串联电压调节器
    结构：
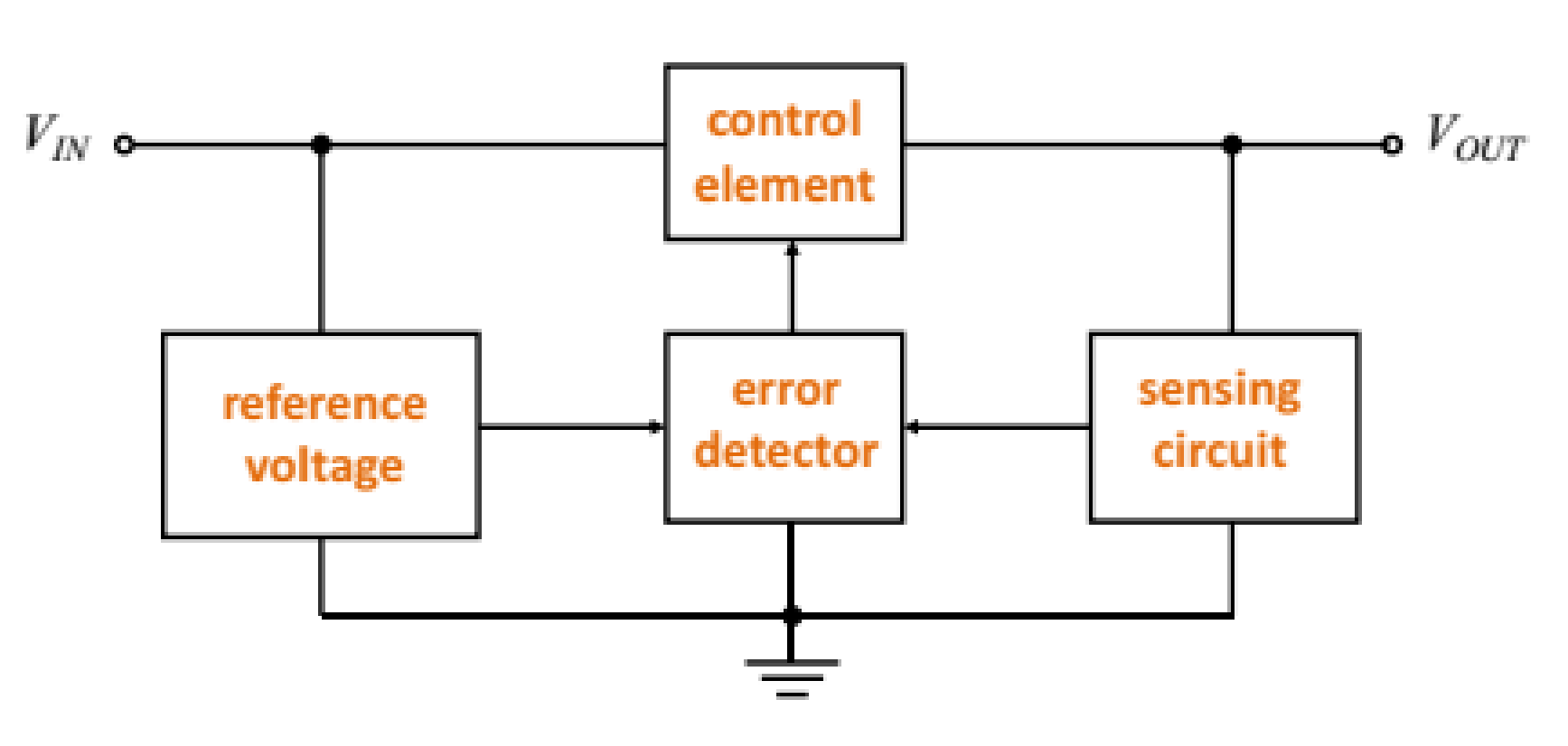
  3. 调整晶体管电路
    结构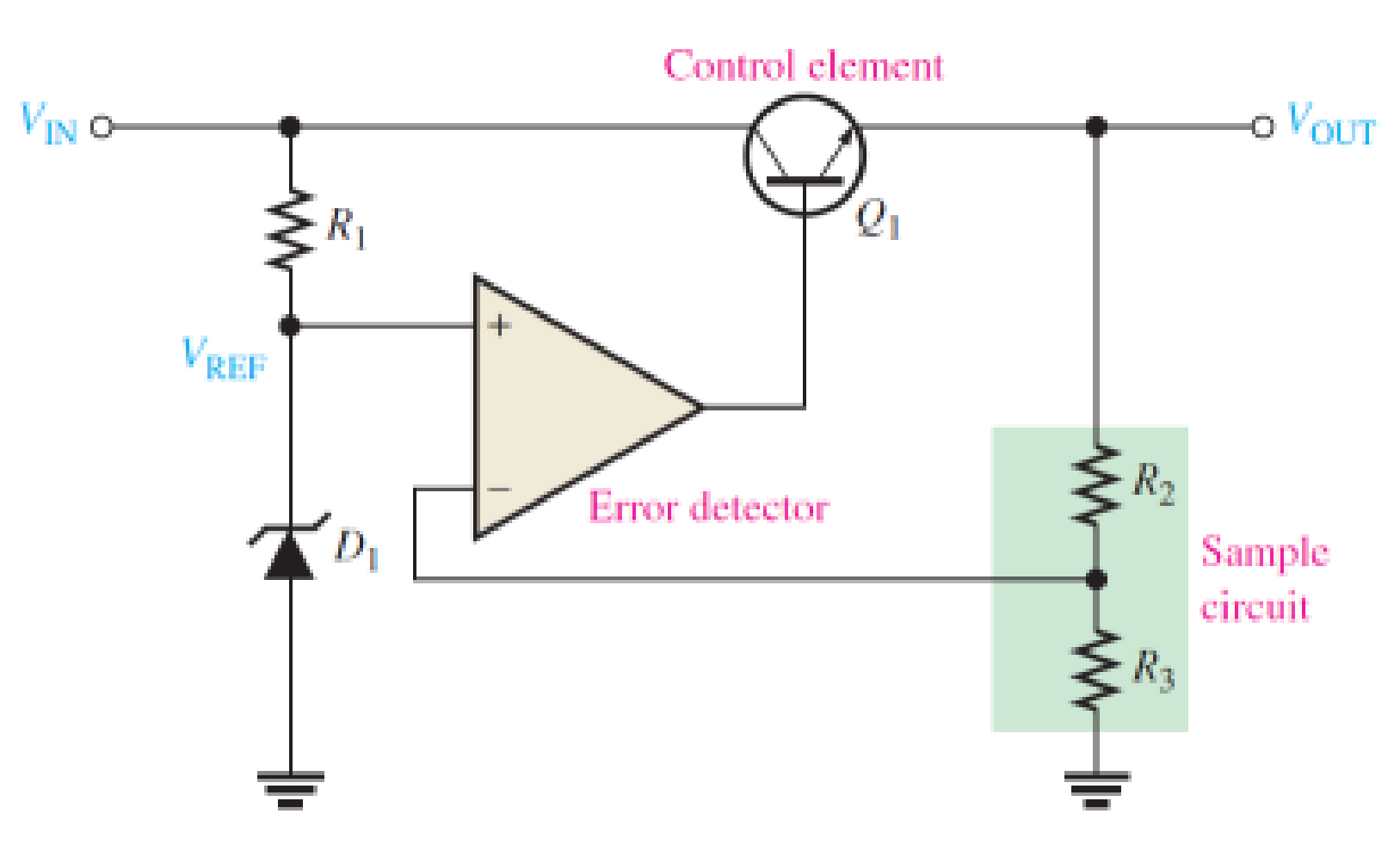： 原理：
    肖克利二极管为运算放大器的+提供稳压的作用。
    当\(V_{out}\)因为各种原因上升时，与之相连接的分压器\(R_2-R_3\)会分走一部分电压，对于放大器的反相输入端\(V_-=\frac{R_3}{R_2+R_3}\),\(V_-\)上升，对于整个运算放大器的输入端，有： \[V_{in}(↓)=V_+(-)-V_-(↑)\]
    因此输出端\(V_{out}=V_{B}\)下降，对于可控晶体管，其\(V_B(↓)\)导致\(V_E(↓)\),最终调整\(V_{out}(↓)\)。
    与此同时，\(V_C(↓)\)使得\(V_{REF}(↑)\),使得\(V_+\)上升，但由于肖克利二极管的存在\(V_+\)的上升幅度不明显。
学习笔记 > 电路与器件
常考知识点
https://l61012345.top/2021/03/15/学习笔记/电路与器件/电路与器件/
作者
Oreki Kigiha
发布于
2021年3月15日
更新于
2023年10月20日
许可协议