03. 极坐标图/奈奎斯特图的绘制和分析
本文最后更新于 2023年10月20日 上午
极坐标图/奈奎斯特图的绘制和分析
正弦输入时的系统输出
二阶线性系统的转换方程可以表示为:
\[T(s)=\frac{Kω_n^2}{s^2+2ζω_ns+ω_n^2}\] 系统输入为正弦信号\(r(t)=Asinωt\)是工程中最常见的情况,此时系统的输出为:
\[C(s)=\frac{Kω_n^2}{s^2+2ζω_ns+ω_n^2}\frac{Aω}{s^2+ω^2}\] 对其进行拉普拉斯反变换后得到\(c(t)\),改变\(ω\)的值,可以发现系统的瞬态响应的幅值和相位随着\(ω\)的变化而变化:
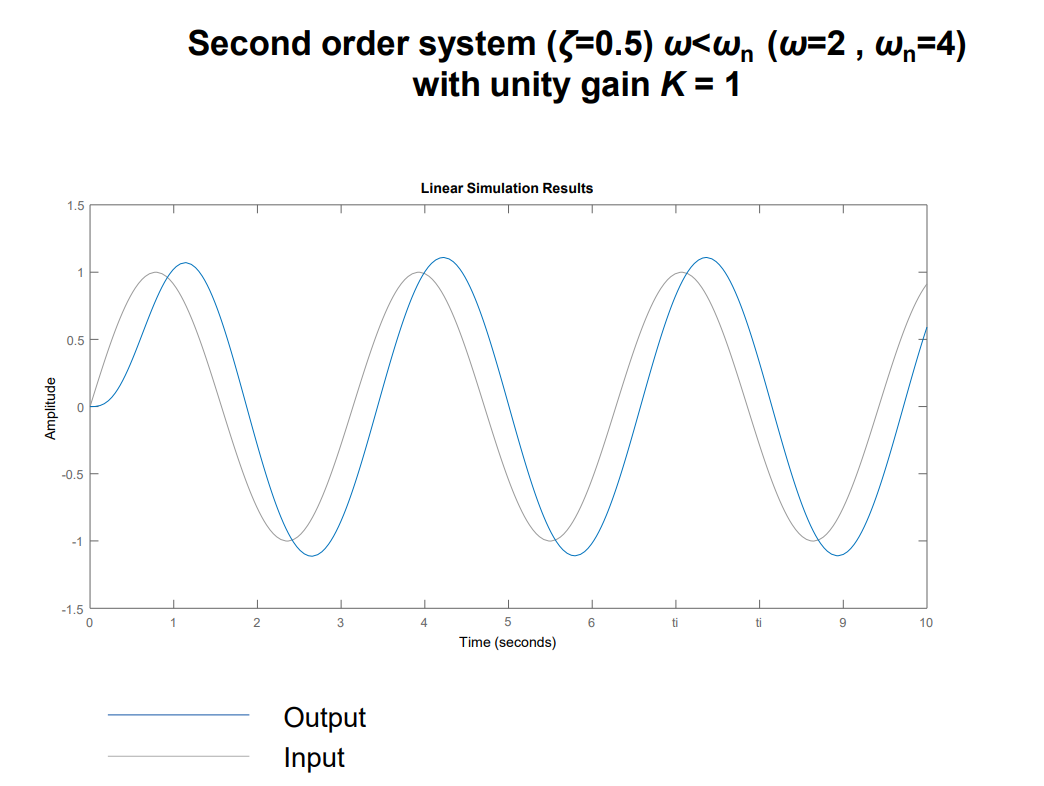
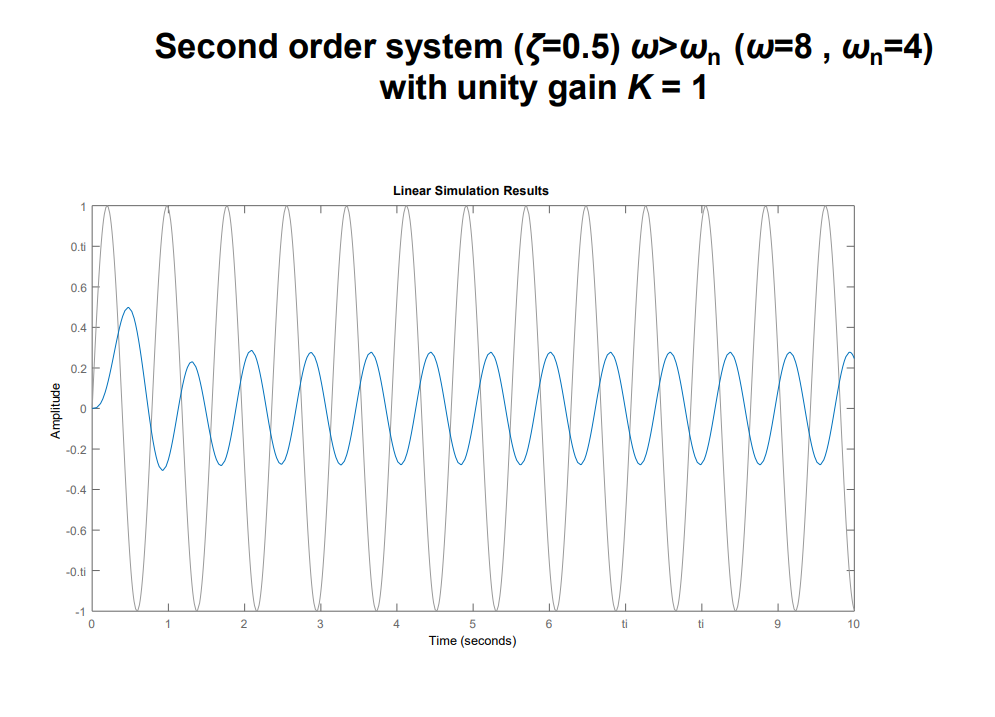
对于稳定系统,可以发现当输入为正弦信号时,系统输出最终都会收敛到某个正弦信号上,最终收敛到的正弦信号参数与输入的正弦信号的幅值和相位是不同的,且随着输入频率\(ω\)的变化而变化,像这样的系统输出随着系统输入信号频率变化而变化的响应称为系统的频率响应,它分为系统的幅度值-频率响应,简称幅频响应(Magnitude frequency response)和系统的相位-频率响应,简称相频响应(Phase frequency response)两部分。
输入信号的频率\(ω\)会改变系统的瞬态响应的幅值和相位,有必要对系统进行进一步的研究以定量分析这种影响。
系统的频率响应概述
对系统的转换方程\(H(s)\),根据s域定义\(s=jω,j^2=-1\),得到:
\[H(jω)=H(s)|_{s=jω}\] \(H(jω)\)称为系统的频率响应。
定义系统方程\(H(jω)\)的幅度值-频率响应为其转换方程的绝对值表达:
\[|H(jω)|\] 以分贝形式表达为:
\[|H(jω)|_{dB}=20lg|H(jω)|\] 系统方程\(H(jω)\)的相位-频率响应为其转换方程的实部和虚部组成的夹角:
\[∠H(jω)=arctan\frac{Im[H(jω)]}{Re[H(jω)]}\] 系统的频率响应可以由幅频响应和相频响应两部分表示:
\[H(jω)=|H(jω)|e^{j∠H(jω)}\] 系统的频率响应、幅频响应和相频响应在复平面上可以表示为:
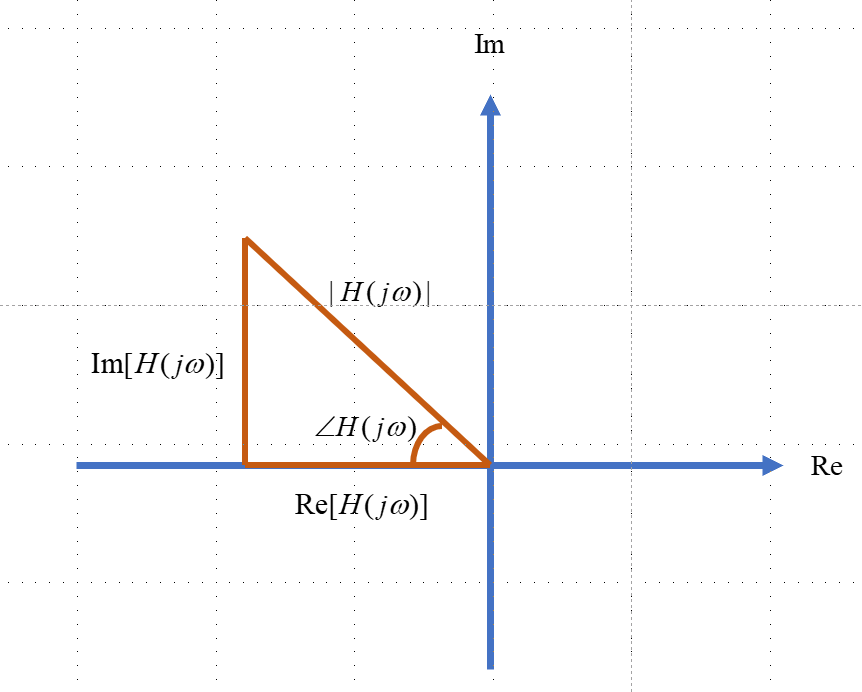
由于系统的频率响应本来就是一个复函数,因此可以通过对分母乘以共轭项的方式分离出频率响应的实部和虚部。根据勾股定理即可找到系统的幅频响应和相频响应。
例如一阶单位反馈控制系统\(H(jω)=\frac{K}{1+jωT}\),有:
\[H(jω)=\frac{K}{1+jωT}\frac{1-jωT}{1-jωT}=\frac{K}{1+ω^2T^2}-j\frac{KωT}{1+ω^2T^2}\] 由勾股定理:
\[\begin{aligned}
|H(jω)|=&\sqrt{\left(\frac{K}{1+ω^2T^2}\right)^2+\left(-\frac{KωT}{1+ω^2T^2}\right)^2}\\
=&\frac{K}{\sqrt{1+ω^2T^2}}
\end{aligned}\] \[∠H(jω)=arctan(\frac{-KωT}{K})=arctan(-ωT)\]
极坐标图
系统的幅频响应和相频响应可以视作极坐标,进而能够通过系统的幅频响应和相频响应在极坐标系上形成的轨迹来表示系统的频率响应。
\[(ρ,θ)=(|H(jω)|,∠H(jω))\] 根据系统的频率响应、幅频响应和相频响应的几何关系,上述极坐标也可以等效为: \[(Re,Im)=(Re[H(jω)],Im[H(jω)])\] 比如,一阶单位反馈控制系统的极坐标可以表示为:
\[(\frac{K}{\sqrt{1+ω^2T^2}},arctan(-ωT))|_{polar}↔(\frac{K}{1+ω^2T^2},-\frac{KωT}{1+ω^2T^2})\] 每一个特定的\(ω\)值:\(ω=ω_1\)在极坐标上都是一个唯一的点,所有点连接而成的轨迹即可表示系统的频率响应。
此外,系统方程的轨迹上还需要用箭头标示出从\(ω=0\)到\(ω=∞\)的箭头,以反映系统随频率的变化。
因此极坐标图有两种:一种以\((Re,Im)=(Re[H(jω)],Im[H(jω)])\)为理论基础,绘图为直角坐标图:横轴为实轴,纵轴为虚轴。另一种以\((\frac{K}{\sqrt{1+ω^2T^2}},arctan(-ωT))|_{polar}\)为理论基础,图为极坐标图。
极坐标图如下图所示:
直角坐标
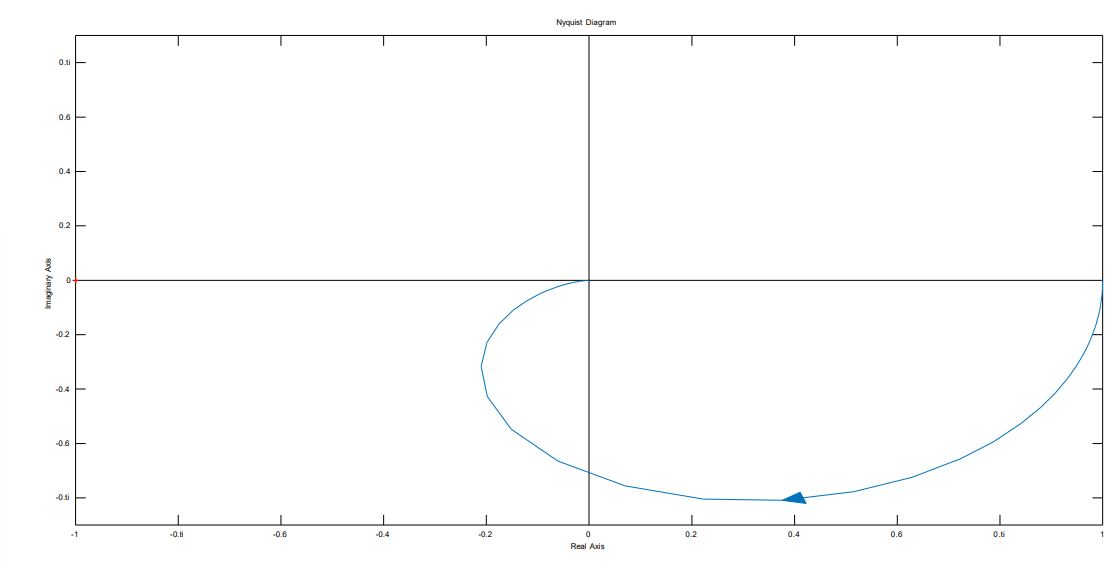
极坐标
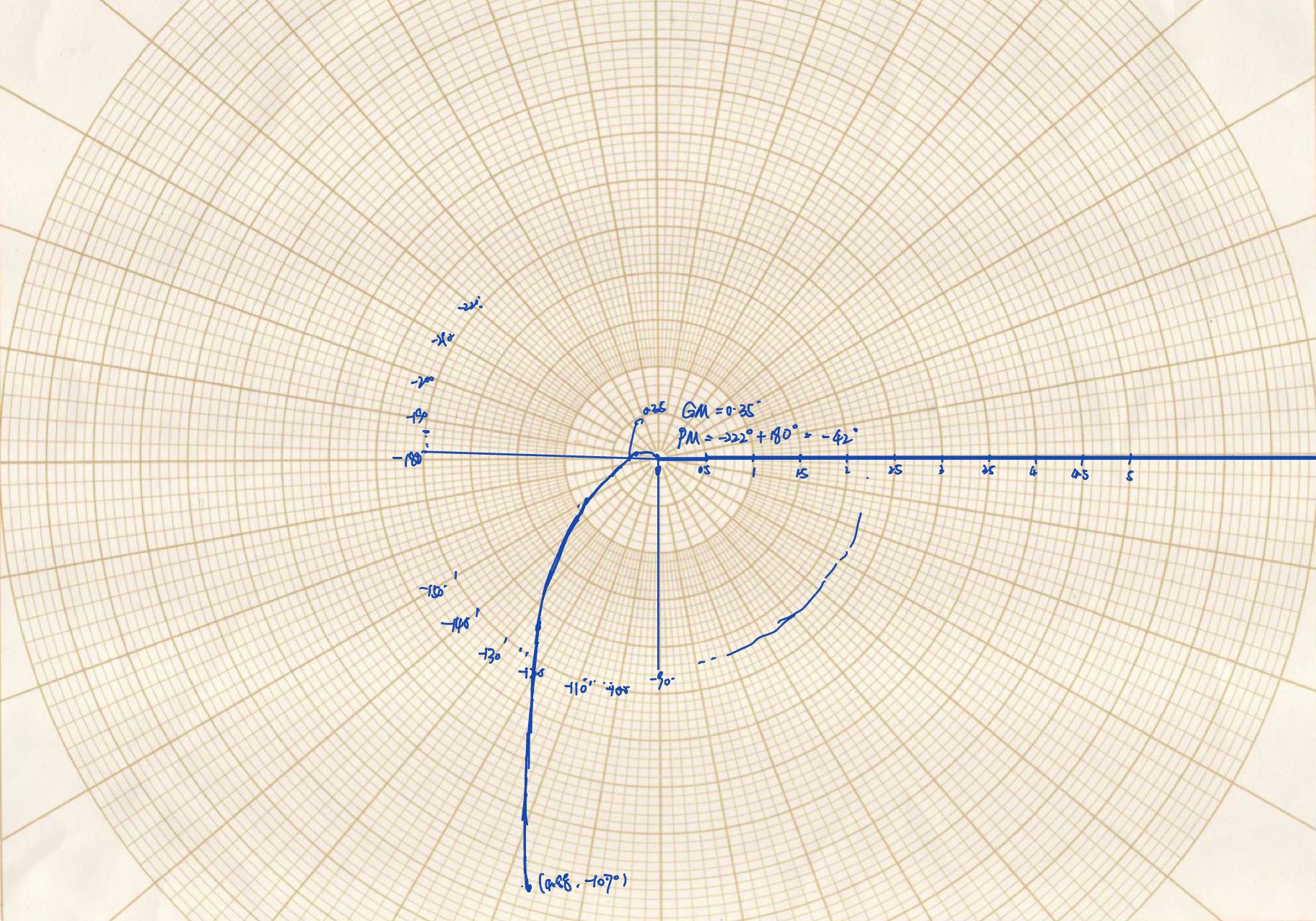
极坐标图最大的优点是能够在一张图上同时反应幅度值和相位随着频率的变化情况。
极坐标图(直角坐标)的画法
- 对\(H(jω)\)分子分母同时乘以分母的共轭部分,并\(H(jω)\)的分离出实部和虚部
- 找到\(ω=0\)在极坐标上点
- 找到\(ω=∞\)在极坐标上的点
- 列方程,找到实部\(Re[H(jω)]=0\)时对应的\(ω\),并在极坐标上找到对应的点
- 列方程,找到虚部\(Im[H(jω)]=0\)时对应的\(ω\),并在极坐标上找到对应的点
- 找到可能的\(ω\)为其他值时在极坐标上对应的点
- 从\(ω=0\)的点开始,划出连接所有点的轨迹,直到最终到达\(ω=∞\)的点,并标出箭头
方程\(Re[H(jω)]=0\)和\(Im[H(jω)]=0\)根的个数决定了频率响应曲线会穿过坐标轴多少次。
使用卡西欧计算器fx-991CN X辅助绘制极坐标图
- 开机,按【菜单/设置】键进入菜单,按【7】进入表格模式
- 表格模式中显示\(f(x)\),输入\(Re[H(jω)]\)的表达式,其中\(ω\)以【\(x\)】表示,输入完成后按【=】键
- 显示\(g(x)\),输入\(Im[H(jω)]\)的表达式,其中\(ω\)以【\(x\)】表示,输入完成后按【=】键
- 显示“表格范围”,设置\(x\)的取值范围,使用【↑】【↓】选择输入对象,输入合适的开始值、终止值和步长,每一项输入完成后按【=】键
- 按下【=】键,计算器会得出从起始值到终止值,每隔一个步长的\(x_i\)所对应的\(f(x_i)\)和\(g(x_i)\),根据此进行作图
极坐标图(极坐标)的画法
- \(H(jω)\)分子分母同时乘以分母的共轭部分,并\(H(jω)\)的分离出实部和虚部
- 对\(H(jω)\)求解出\(|H(jω)|\)和\(∠H(jω)\)
- 使用卡西欧计算器fx-991CN X的表格模式,设置\(f(x)\)和\(g(x)\)分别为\(|H(jω)|\)和\(∠H(jω)\),并设置合适的步长和终点,输入完成后按【=】键,得到极坐标绘图所需的表格
- 按照表格在极坐标纸上描点连线即可
这种方法绘制起来比较困难,建议使用直角坐标进行绘图。
奈奎斯特稳定判据
极坐标图的优点是能用一条曲线同时反映系统的幅频响应和相频响应,但是相比于波特图,极坐标图无法直接通过观察曲线走向得到系统的稳定性分析,因此需要引入奈奎斯特稳定性判据理论,以此对极坐标图进行改进,改进后的极坐标图称为奈奎斯特图,其优点是用一条曲线同时反映系统的幅频响应和相频响应,也能够通过曲线直接判断系统的稳定性。
本节参考:
[奈奎斯特稳定判据 西安交通大学-刘剑毅]https://gr.xjtu.edu.cn/c/document_library/get_file?folderId=1797493&name=DLFE-28935.pdf
[知乎:奈奎斯特稳定判据]https://zhuanlan.zhihu.com/p/33007435
柯西辐角原理
根据三角函数\(y=sinx\)的定义,一个矢量逆时针旋转一圈时,对应的三角函数相位角变化为\(2π\),如下图所示:
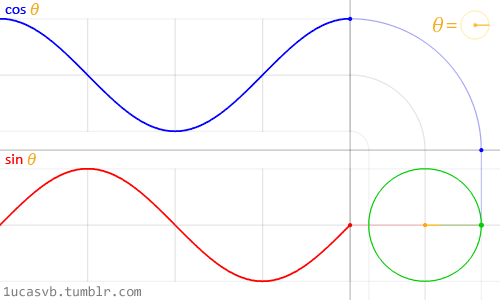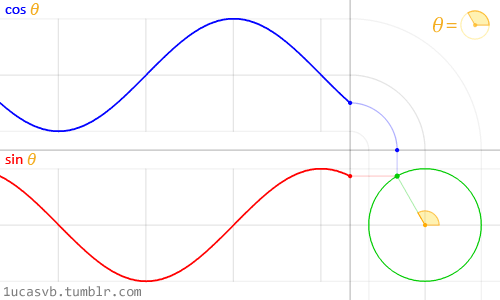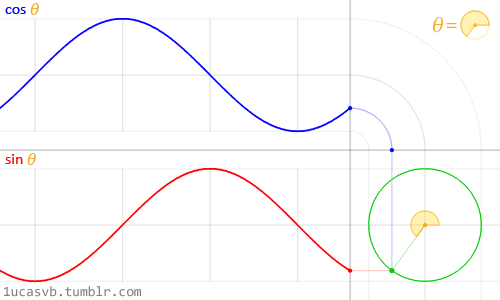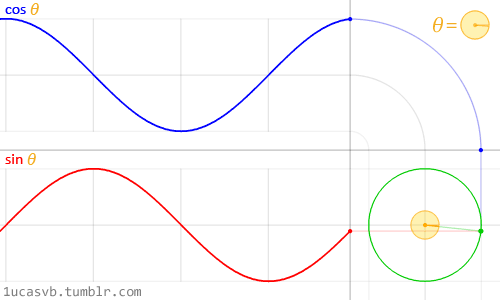
对复变函数:
\[F(s)=\frac{Y(s)}{X(s)}=\frac{K∏(s+z_i)}{∏(s+p_i)}\] 有复变函数的辐角表示为复变函数所有零向量\(Δ(s+z_i)\)(s域上\(s\)到某一零点\(z_i\)的矢量)的角度和减去所有极向量\(Δ(s+p_i)\)(s域上\(s\)到某一极点\(p_i\)的矢量)的角度和:
\[∠F(s)=∑Δ(s+z_i)-∑Δ(s+p_i)\]
柯西辐角原理(Cauchy’s Argument Principle)首先提出了一个前提:
使用映射律\(s→F(s)\)对每一个\(s\)进行映射时:s域(σ-jω)上除了极点外的每一点,在\(F(s)\) 平面(Re-Im)上都有一点能够与之对应。如果s域内有一条顺时针运动的闭合曲线,那么\(F(s)\)平面上也必然有一条与其对应的闭合曲线,其旋转方向取决于函数\(F(s)\)的性质。
那么,根据这个前提有如下推论:
- s域内的闭合曲线包围\(F(s)\)的一个零点\(z_i\),曲线运动方向为顺时针旋转一周,其相位角变化为-2π,其他矢量角变化为0。根据\(∠F(s)=∑Δ(s+z_i)-∑Δ(s+p_i)\),则\(F(s)\)的相位角变化为-2π。即\(F(s)\)绕\(F(s)\)平面原点逆时针旋转一周。
- s域内的闭合曲线包围\(F(s)\)的一个极点\(p_i\),曲线运动方向为顺时针旋转一周,其相位角变化为-2π,其他矢量角变化为0。根据\(∠F(s)=∑Δ(s+z_i)-∑Δ(s+p_i)\),则\(F(s)\)的相位角变化为2π。即\(F(s)\)绕\(F(s)\)平面原点顺时针旋转一周。
从上述推论可以得到:
s域上的闭合曲线如果包围了\(F(s)\)的\(Z\)个零点、\(P\)个极点,并且闭合曲线不通过\(F(s)\)的任何零点或者极点,当\(s\)沿着闭合曲线顺时针运动一周,在\(F(s)\)对应包围原点的闭合圈数\(N\)为:
\[N=P-Z\] \(N>0\)表示逆时针包围圈数,\(N<0\)表示顺时针包围圈数。
该结论称为柯西辐角原理。
奈奎斯特路径
尽管有些资料对极坐标图和奈奎斯特图的概念不做区分,但事实上两者是不一样的。本章中认为奈奎斯特图中应当包含频率响应的镜像部分以及频率从\(0^-\)到\(0^+\)变化时系统的频率响应轨迹。
奈奎斯特路径为一段在s域上的闭合矢量路径,其涵盖了s域的右半轴,如下图所示:
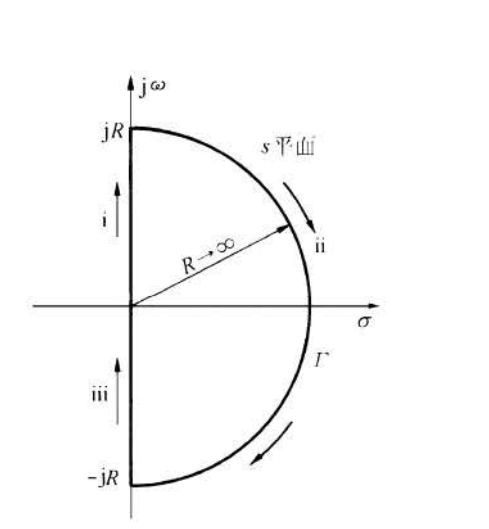
奈奎斯特路径为分为三部分:
- i:频率\(ω\)由\(0^+\)变化到\(+∞\),则\(s=jω+σ\)运动轨迹为(i).
- ii:除虚轴以外的整个右半平面,\(s=jω+σ=Re^{jθ},R=∞\),角度\(θ\)由\(\frac{π}{2}\)变化到\(-\frac{π}{2}\).
- iii: 频率\(ω\)由\(∞^-\)变化到\(0^-\),则\(s=jω+σ\)运动轨迹为(iii).
奈奎斯特路径的特殊情况
如果系统的开环极点在奈奎斯特路径的i和iii上,则奈奎斯特路径需要绕过:
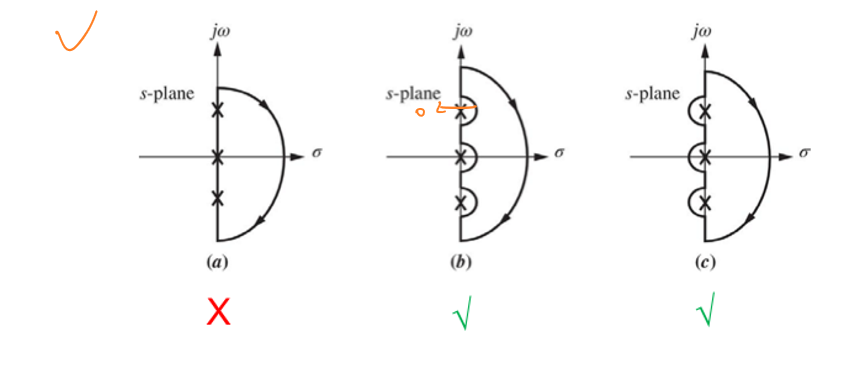
每一个绕路的小半圆可以表示为\(\lim_{ρ→0}ρe^{jθ}\)。
系统传递函数的映射
对系统\(T(s)\),
有系统的开环传递函数: \[T_{ol}=G(s)H(s)=\frac{B(s)}{A(s)}\] 其中\(B(s)=∏(s+z_i),A(s)=∏(s+p_i)\).
系统的闭环传递函数:
\[T_{cl}(s)=\frac{G(s)}{1+G(s)H(s)}=\frac{A(s)G(s)}{A(s)+B(s)}\] 可以发现\(A(s)+B(s)\)为闭环传递函数得出极点的多项式。
定义
\[F(s)=1+G(s)H(s)\] 表示系统的特征多项式,有:
\[F(s)=\frac{A(s)+B(s)}{A(s)}=\frac{闭环极点}{开环极点}\] 讨论使用\(F(s)\)映射奈奎斯特路径:
- i:\(ω\)由\(0^+\)变化到\(+∞\)时\(F(s)\)的变化对应\(F(s)\)的频率响应。根据\(F(s)=1+G(s)H(s)\),\(F(s)\)的频率特性实则为开环传递函数的频率响应向右平移一个单位。
- ii: \(s=Re^{jθ},R=∞\),角度\(θ\)由\(\frac{π}{2}\)变化到\(-\frac{π}{2}\)对应\(F(s)→1\)
- iii:\(ω\)由\(∞^-\)变化到\(0^-\)时\(F(s)\)的变化对应\(F(s)\)的频率特性以实轴对称的镜像.
通过上述方式就可以绘制出奈奎斯特路径在\(F(s)\)上的映射,根据柯西辐角原理以及对函数\(F(s)\)的定义:
\[F(s)=\frac{A(s)+B(s)}{A(s)}=\frac{闭环极点}{开环极点}\] 可以重新建立柯西辐角原理公式:
\[N=P-Z\] 由于奈奎斯特路径在\(s\)域上只包含s域的右半轴部分,因此: \(Z\)为\(F(s)\)在s域右半轴的零点,是系统\(T(s)\)在s域右半轴的闭环极点(即\(\frac{G(s)}{1+G(s)H(s)}\)的极点),\(P\)为\(F(s)\)在s域右半轴的极点,是系统\(T(s)\)在s域右半轴的开环极点(即\(G(s)H(s)\)的极点),\(N\)为奈奎斯特路径在\(F(s)\)上的映射轨迹包围\(F\)域原点\((0,0)\)的次数。
改写上述公式:
\[Z=P-N\] 根据系统的稳定性准则:当系统的闭环传递函数中所有的极点都位于s域左半轴时,系统是稳定的。那么,当\(Z=0\)时,系统在s域右半轴不存在任何极点,表明系统是稳定的。
根据\(F(s)=1+G(s)H(s)\),\(F\)平面上奈奎斯特曲线包围原点的情况等于\(GH\)平面上奈奎斯特曲线包围\((-1,0)\)的情况。因此,只需要研究开环传递函数包围\((-1,0)\)的情况,就可以得出闭环系统的稳定性。
此时\(N\)应当表述为奈奎斯特路径在\(G(s)H(s)\)上的映射轨迹包围\(GH\)域\((-1,0)\)的次数。
总结奈奎斯特稳定判据为:
当频率\(ω\)从\(-∞\)向\(+∞\)变化时,\(GH\)平面上奈奎斯特曲线包围点\((-1,0)N\)次,当 \[Z=P-N=0\] 其中\(P\)为系统开环传递函数\(G(s)H(s)\)的在s域右半轴的极点个数
\(N\)拥有极性,逆时针包围点\((-1,0)\)时\(N>0\),顺时针包围点\((-1,0)\)时\(N<0\)
系统在s域右半轴不存在任何极点,表明系统是稳定的。
某些资料上N的极性与此处所述相反,判别式为\(Z=P+N=0\),且\(N\)代表半圈数而非完整圈数。本课程认为根据三角函数定义和相角变化,在逆时针包围时作为\(N>0\)更为合理。而奈奎斯特路径和辐角定理的条件都是闭合曲线,因此\(N\)代表整个圈数更为合理。
因此,根据奈奎斯特稳定判据判断系统稳定的方法:
- 找到系统开环传递函数\(G(s)H(s)\)的在s域右半轴的极点个数\(P\)。
- 画出奈奎斯特曲线,并且找到\(N\)。
- 利用\(Z=P-N\),判断\(Z\)是否为0,得出稳定性结论。
奈奎斯特曲线的画法
从上述结论来看,要画出\(G(s)H(s)\)的奈奎斯特曲线,才能够找到\(N\)的值。奈奎斯特曲线的画法如下:
- 绘制出\(G(s)H(s)\)的极坐标图,代表\(G(s)H(s)\)的频率响应曲线,对应路径i
- 绘制出\(G(s)H(s)\)的频率响应曲线以实轴为对称轴的镜像,对应路径iii
- 路径ii(奈奎斯特图上从\(0^-\)到\(0^+\)的路径)在\(F(s)\)中对应原点(0,0)。
- 此外,如果系统的开环极点在奈奎斯特路径的i和iii上,此时这段绕过的路径对应将路径i和iii的映射以\(R→∞\)的半圆首尾(\(0^-→0^+\))连接的路径。

- 路径ii(奈奎斯特图上从\(0^-\)到\(0^+\)的路径)在\(F(s)\)中对应原点(0,0)。
第三步补充路径的方法如下图所示:
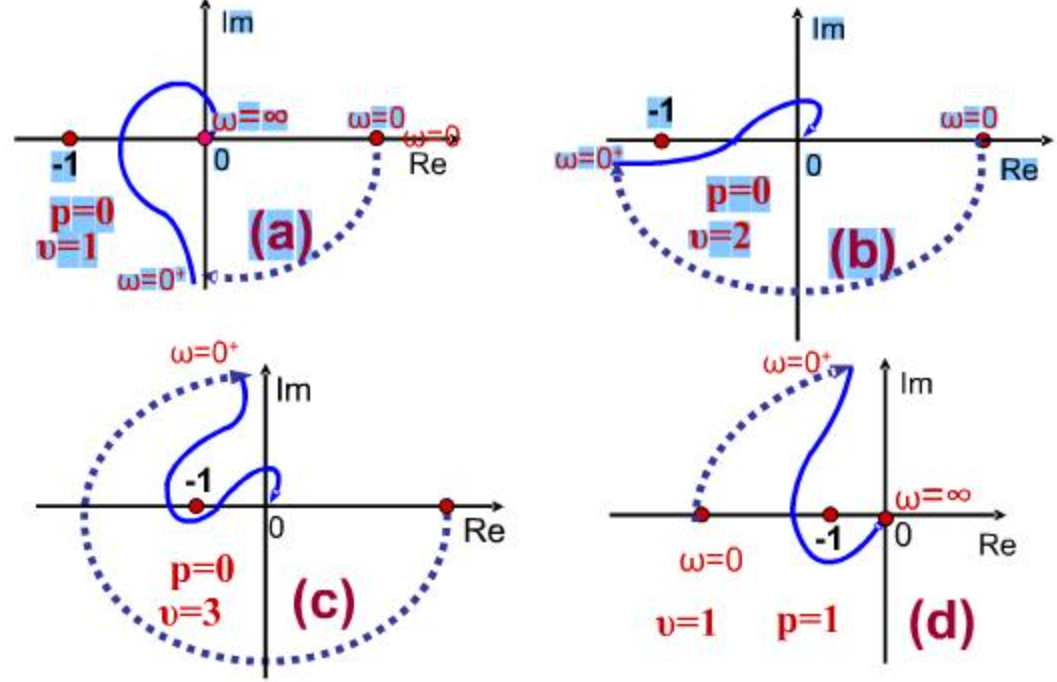
如下图表示了\(G(s)=\frac{1}{s(s+1)}\)的奈奎斯特图:
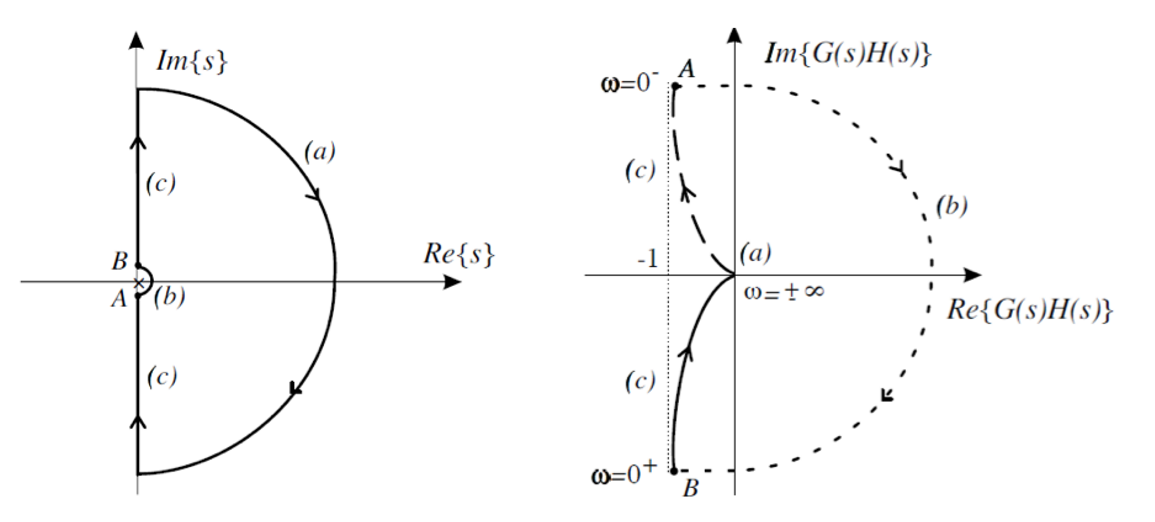
奈奎斯特图特征
根据稳定性判断系统传递函数参数
对系统开环传递函数\(G(s)=\frac{K}{∏(s+p_i)}\),如果系统稳定,那么\(N=P\)。需要找到奈奎斯特曲线与实轴的所有交点:\((c_i,0)\),并判断其与\(-\frac{1}{K}\)的大小,根据\(N=P\)的临界条件来确定\(K\)的取值范围。
当奈奎斯特曲线正好穿过点(-1,0)时,系统处于临界稳定状态,系统的稳定和不稳定处于随机中。
增益裕量和相位裕量
定义增益裕量(Gain margin)\(G_m\)为使得系统处于临界稳定状态的增益。增益裕度可以通过奈奎斯特图上表示为相位角为\(-180°\)时对应的幅值\(-\frac{1}{a}\)求得:
\[G_m|_{dB}=20lg(a)\] 定义相位裕量(Phase margin)\(P_m\)为使得系统处于系统处于临界稳定状态的相位。相位裕量可以通过奈奎斯特图上单位圆与奈奎斯特图交点连线与实轴的负半轴夹角测量得到,如下图所示:
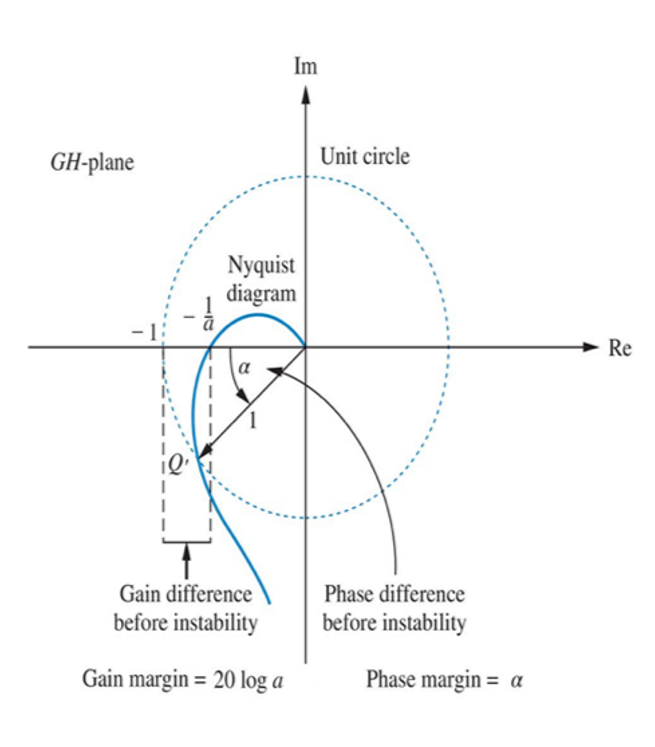
灵敏度函数
如果开环传递函数为\(G(s)H(s)\),定义系统的灵敏度函数(sensitivity function)为:
\[S(s)=\frac{1}{1+G(s)H(s)}\] 灵敏度函数的最大值\(M_{s}\)可以反应系统的鲁棒性。而灵敏度穿越频率(sensitivity crossover frequency)指灵敏度函数幅值为1时对应的角频率,以\(ω_{sc}\)表示。
在奈奎斯特图上,\(1+GH\)可以表示为-1到奈奎斯特曲线的向量,\(\frac{1}{M_{s}}\)是-1到奈奎斯特曲线的最短距离。
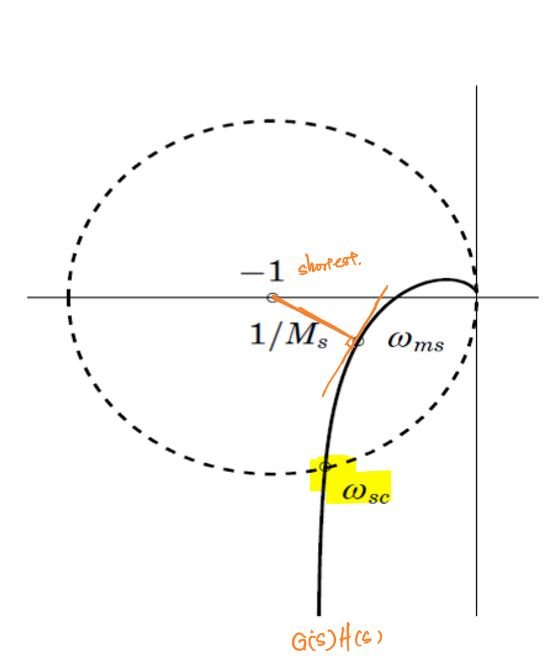
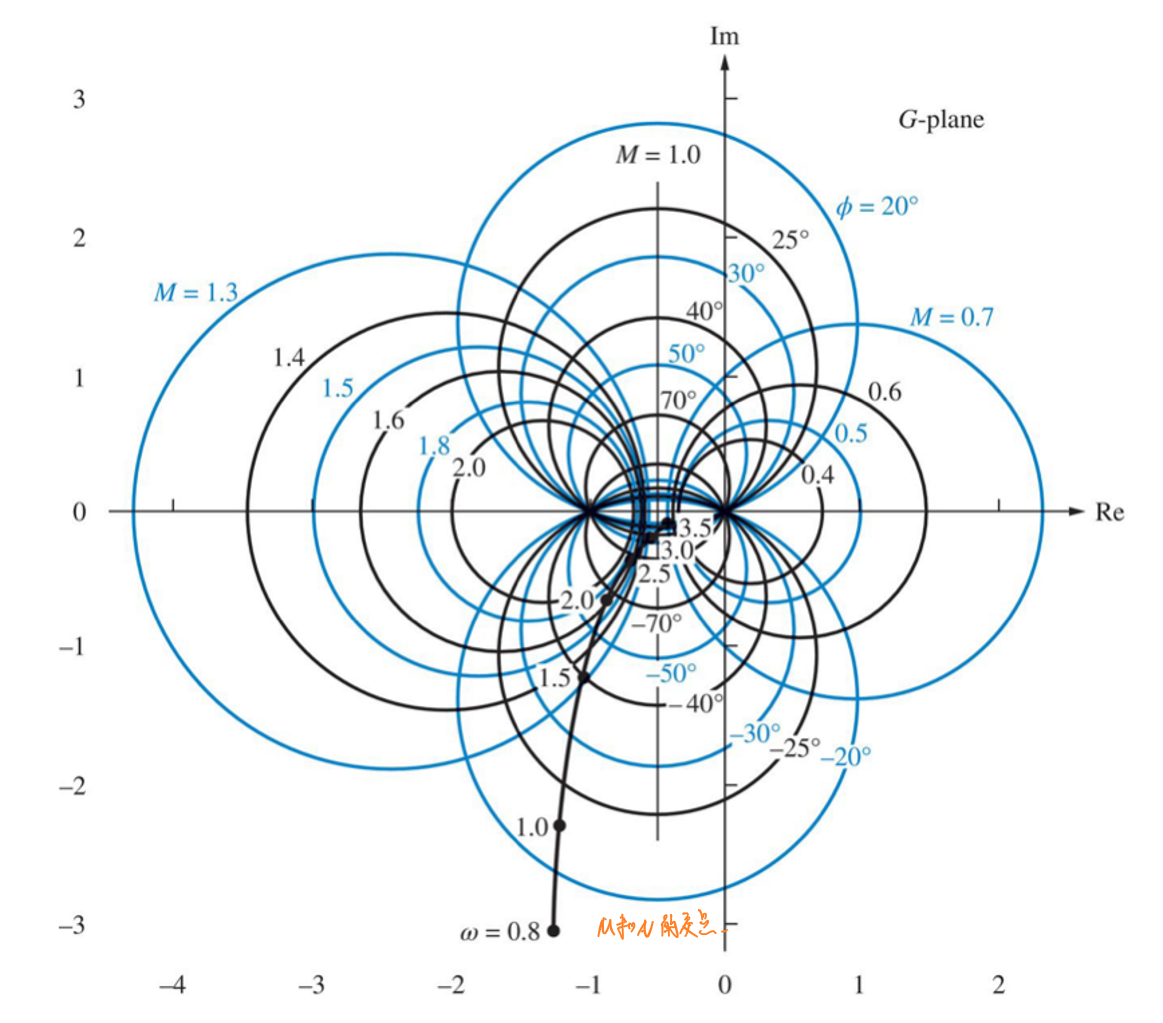
M环和N环
M环和N环是单位反馈系统的幅频响应和相频响应的轨迹。对于单位反馈系统,其闭环传输函数为:\(T(s)=\frac{G(s)}{1+G(s)}\)。其中\(G(s)=P(s)+jQ(s)\).
有:
\[T(jω)=\frac{P(ω)+jQ(ω)}{P(ω)+1+jQ(ω)}\] 定义:
\[M^2=|T^2(jω)|=\frac{P^2(ω)+Q^2(ω)}{(P(ω)+1)^2+Q^2(ω)}\] 重新整理后可得:
\[(P+\frac{M^2}{M^2-1})^2+Q^2=\frac{M^2}{(M^2-1)^2}\] 可以发现这是一个半径为\(\frac{M}{M^2-1}\),以\((-\frac{M^2}{M^2-1},0)\)形成的圆的轨迹。这个圆随着M的变化而变化:
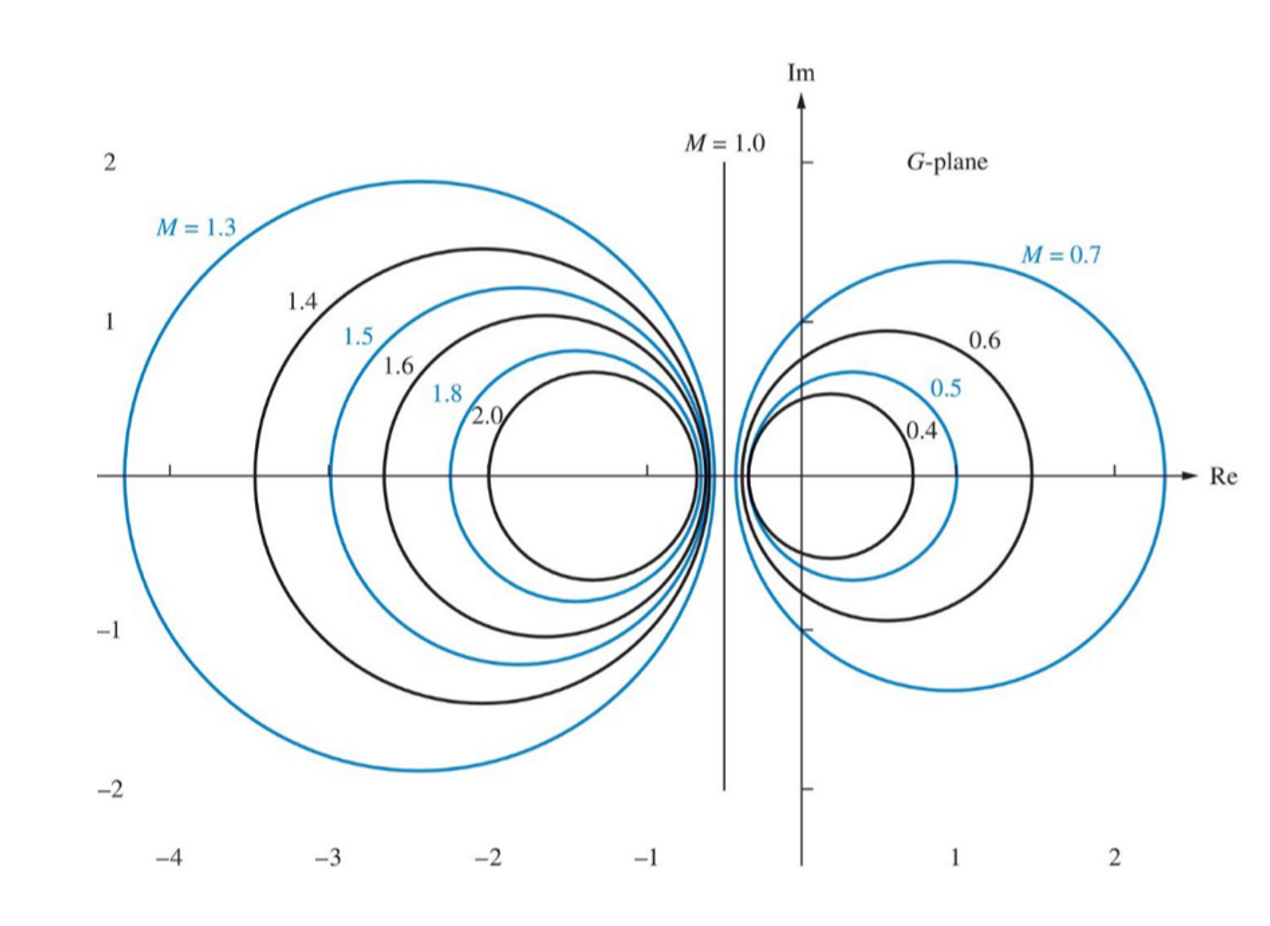
同理可以得到反映单位控制系统相位变化的N环:
\[φ=arctan\frac{\frac{Q}{P}-\frac{Q}{P+1}}{1+\frac{Q}{P}\frac{Q}{P+1}}\] \[(P+\frac{1}{2})^2+(Q-\frac{1}{2N})^2=\frac{N^2+1}{4N^2}\] 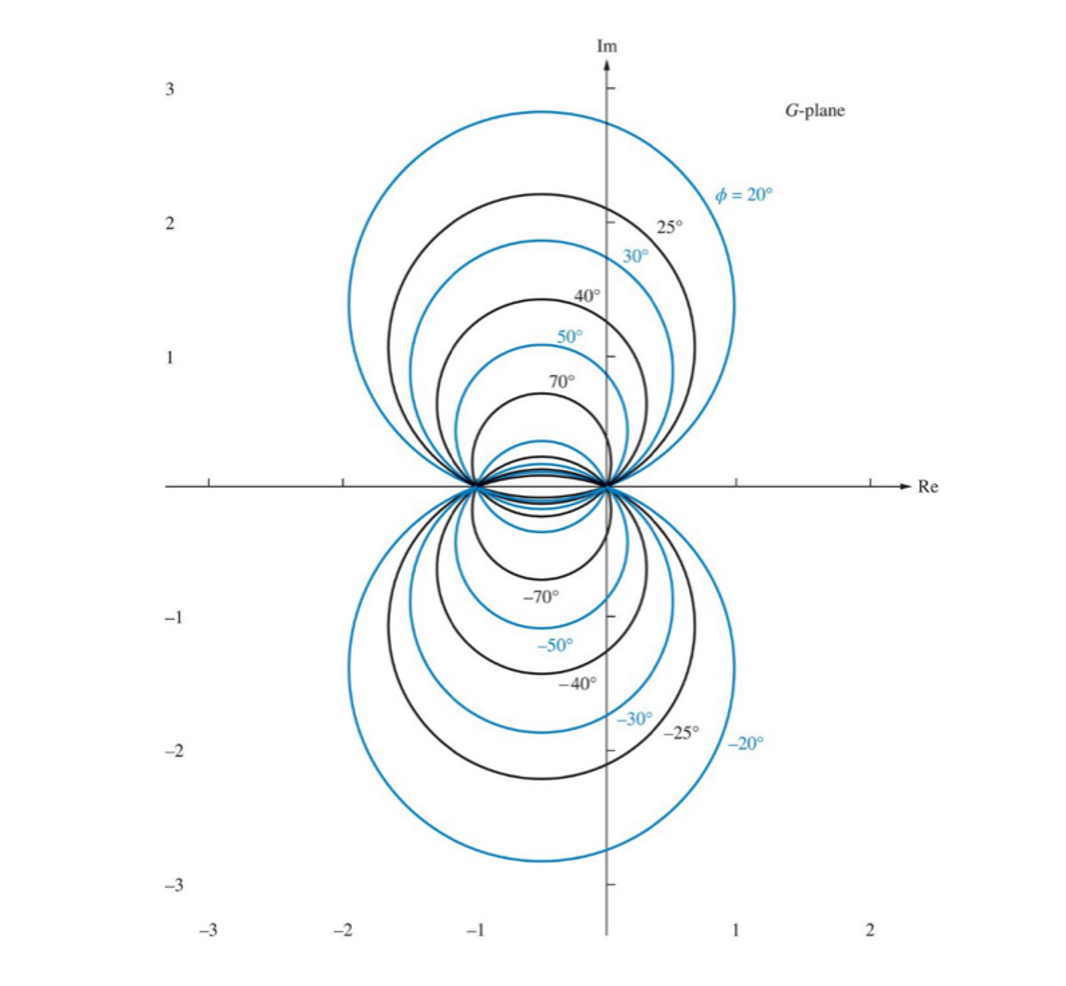
可以发现,系统的闭环响应可以通过系统的奈奎斯特图(由开环传递函数得到)与M环和N环的交点轨迹得到: