5.2. 前向传播模型

前向传播模型

神经元模型

• 假设： 大脑对于不同功能（听觉，视觉，触觉的处理）的实现是依赖于同样的学习方法
  
• 依据： 神经重接实验

神经网络模拟了大脑中的神经元或者是神经网络。先来看大脑中的神经元构成:

如图所示，神经元有很多的输入通道（树突），同时通过轴突给其他的神经元传递信号。大脑中的每一个神经元的树突接收来自多个其他神经元的输入，同时该神经元的轴突向其他神经元输出：

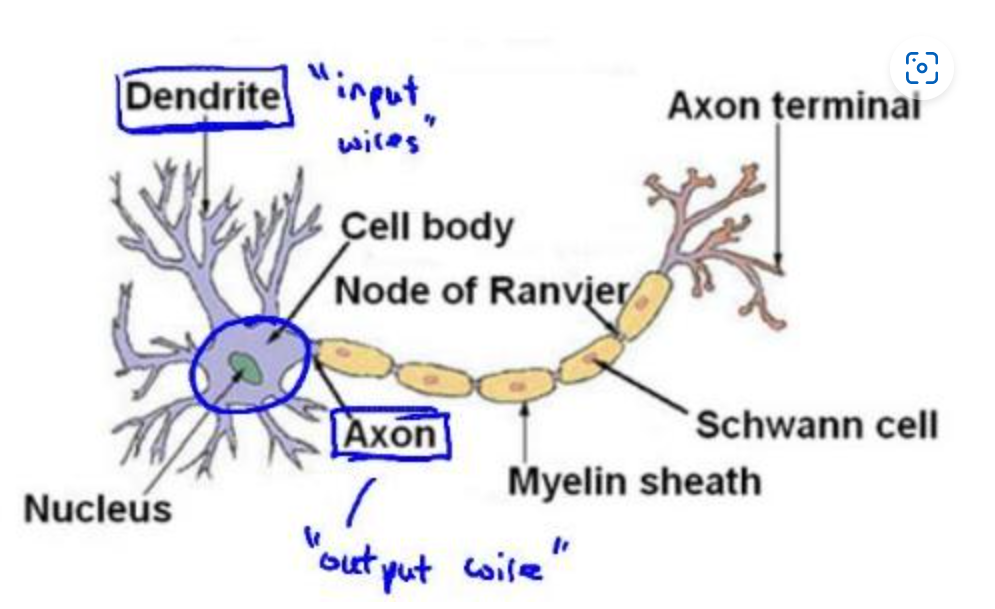
将神经元简单抽象：一个计算单元，它从输入端接收一定数目的信息，并作一些处理，并将结果传递给其他的神经元。
在计算机中，我们构建一个逻辑单元，它从输入端接收数据集X，并作处理来生成一个Sigmoid函数\(h_θ (x)=\frac{1}{1+e^{-θ^T X}}\)：

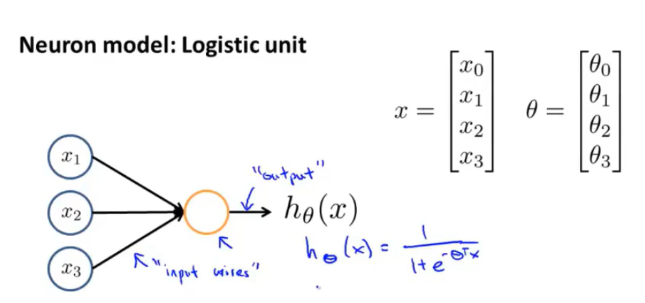
在这个模型之上，输入端会额外增加一个\(x_0=1\)，称为偏置单元(bias unit)。
在神经网络中，\(Θ\)称为模型的权重，\(g(z)\)称为激活函数(activation function)。

激活函数有多种选择，常见的激活函数有：
- Sigmoid函数:\(y=\frac{1}{1+e^{-θ^T X}}\) - 线性函数:\(y=θx\) - 分段线性函数/线性整流单元/ReLU函数：\(y=\begin{cases} 0,x<0\\x,x≥0\end{cases}\) - 高斯函数：\(y=exp(-x^2)\) - 双曲正切函数：\(y=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}\)

本课程中默认提到激活函数时选择的激活函数为Sigmoid函数。

多层神经网络

按照生理学，大脑中的每一个神经元的树突接收来自多个其他神经元的输入，同时该神经元的轴突向其他神经元输出。神经网络模仿了这一生理学特性，它是一组神经元连接在一起的集合，如图所示：

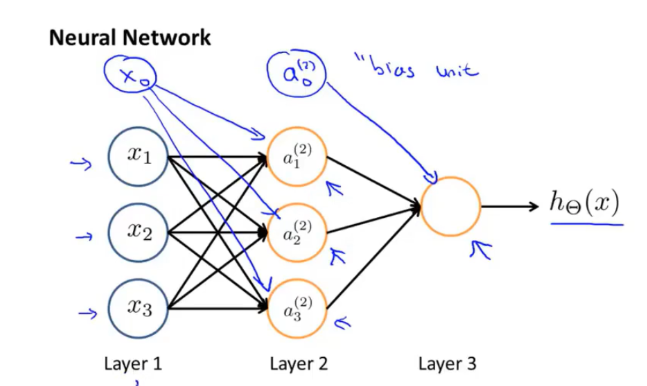
第一层称为输入层，我们在这一层输入全部的特征，最后一层称为输出层，这一层的神经元输出假设的最终结果，中间的层称为隐含层(hidden layer)，隐含层可能不止有一层。

每一层神经元所使用的激活函数必须是相同的。

统一地，将\(a_i^{(j)}\)表示第\(j\)层的第\(i\)个激活项（激活指计算并输出结果），同时，第\(j\)层到第\(j+1\)层之间的映射由参数矩阵\(Θ^{(j)}\)确定。
对于神经网络中第\(j\)层的每一个神经元，其输出可以表示为：
\[a_i^{(j)}=g\left[(∑_{k}Θ_{jk}^{(j-1)}x_k)+b_i\right]\] 其中\(g[·]\)是第\(j\)层的激活函数，\(b_i\)是该神经元的偏置。

如果不考虑偏置，上图的神经网络结构就可以用公式表示为：
\[a_1^{(2)}=g(Θ_{10}^{(1)}x_0+Θ_{11}^{(1)}x_1+Θ_{12}^{(1)}x_2+Θ_{13}^{(1)}x_3)\]
\[a_2^{(2)}=g(Θ_{20}^{(1)}x_0+Θ_{21}^{(1)}x_1+Θ_{22}^{(1)}x_2+Θ_{23}^{(1)}x_3)\]
\[a_3^{(2)}=g(Θ_{30}^{(1)}x_0+Θ_{31}^{(1)}x_1+Θ_{32}^{(1)}x_2+Θ_{33}^{(1)}x_3)\]
\[h_{Θ}(x)=g(Θ_{10}^{(2)}a_0^{(2)}+Θ_{11}^{(2)}a_1^{(2)}+Θ_{12}^{(2)}a_2^{(2)}+Θ_{13}^{(2)}a_3^{(2)})\]
如果一个网络在第j层有\(s_j\)个单元，且在第j+1层有\(s_j+1\)个单元，那么矩阵\(Θ^{(j)}\)的维度为\(s_{j+1} \times (s_j+1)\)

神经网络的向量化

对如上的等式，现在将\(g(·)\)中的线性加权组合以\(z^{(2)}_1,z^{(2)}_2,z^{(2)}_3\)表示，那么就有： \[a_1^{(2)}=g(z_1^{(2)})\]
\[a_2^{(2)}=g(z_2^{(2)})\]
\[a_3^{(2)}=g(z_3^{(2)})\]
现在就能够定义三个向量使得上述等式转化为向量乘法：
\(x= \left[\begin{smallmatrix} x_0 \\\ x_1 \\\ x_2 \\\ x_3 \end{smallmatrix}\right]\), \(z^{(2)}=\left[\begin{smallmatrix} z_1^{(2)}\\\ z_2^{(2)}\\\ z_3^{(2)}\end{smallmatrix}\right]=Θ^{(1)}x\)，\(a^{(2)}=\left[\begin{smallmatrix} a_1^{(2)}\\\ a_2^{(2)}\\\ a_3^{(2)}\end{smallmatrix}\right]\)

那么上述等式最终就可以转化成： \[z^{(2)}=Θ^{(1)}x\]
\[a^{(2)}=g(z^{(2)})\]
对于隐含层的偏置单元，增加一项\(a_0^{(2)}=1\). 最后计算\(z^{(3)}=Θ^{(2)}a^{(2)}\),那么最终得到的假设模型将会是：

\[h_{Θ}(x)=a^{(3)}=g(z^{(3)})\]

单看layer2 和 layer3，事实上，这两层做的就是逻辑回归，但输入进逻辑回归的特征不再是原始的特征\(x\)，而是通过原始特征生成的特征\(a\)。 而\(a\)与\(x\)之间的关系通过\(θ\)来定义。 因此可以通过改变\(θ\)来改变输入层和隐含层之间的关系。

前向传播过程

对于神经网络的训练过程，在每次迭代中，首先需要得到数据集的特征\(x\)输入到神经网络模型后的输出结果，即模型的预测值\(\hat{y}\)，然后根据其真实标签\(y\)返回来调整神经网络中各神经元连接的权重。因此将神经网络的每一次迭代分为前向传播(Forward Propagation/Feedforward Propagation)和反向传播两个过程：前向传播是将数据输入神经网络，然后得到预测值的过程。反向传播则是根据真实值和预测值之间的差距，来调整各连接权重的过程。
简单来说，前向传播的过程即将\(x\)带入到神经网络的表示中，得到输出的过程：
\[h_{Θ}(x)=a^{(N)}=g(z^{(N)})\]
\(N\)表示神经网络最后一层的标识。

下一章将说明如何调整权重\(θ\)的值来优化假设函数。