5.3. 感知机

感知机

神经网络中，单层神经元（无中间层）的计算可用来表示逻辑运算，比如逻辑与(AND)、逻辑或(OR)。这样的单层神经网络被称为感知机(perceptron)。感知机的输入和输出都是二进制数。

线性逻辑函数的实现——AND,OR,NOT

为了解释感知机如何实现逻辑函数的功能，以AND函数为例：

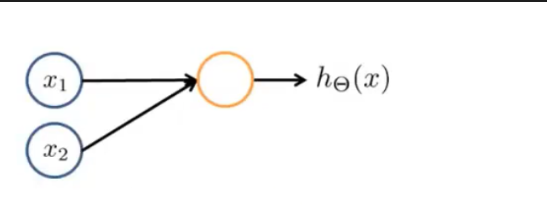
上图表示一个只有两个输入的感知机，输入层有两个特征\(x_1\)和\(x_2\)，它们都应该是二进制数。
目标函数为\(y=x_1 AND x_2\).其激活函数\(g(x)\)设置为sigmod函数。

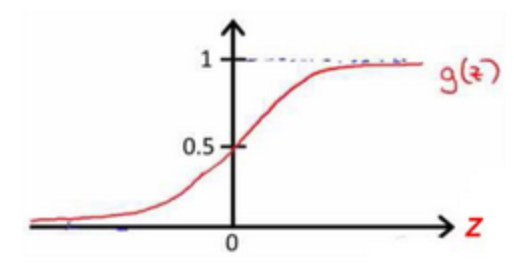
观察sigmoid激活函数\(y=g(x)=\frac{1}{1-e^{-x}}\),可以发现当\(x=4\)时，\(y=0.99\),当\(x=-4\)时，\(y=0.01\)

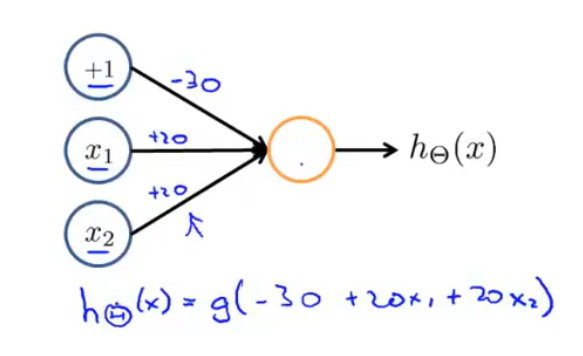
由上述激活函数的性质，为了计算这样的神经网络，首先先增加一个偏置单元 【+1】，对每个单元赋予权重：-30，20,20：

列出真值表：
\[ \begin{array}{lcr} x_1 & x_2 & h_θ(x) \\\ 0 & 0 & g(-30)≈0 \\\ 0 & 1 & g(-10)≈0 \\\ 1 & 0 & g(-10)≈0 \\\ 1 & 1 & g(10)≈1 \\\ \end{array} \]

观察最后一列，最后一列的输出事实上很接近与AND函数的结果，那么可以认为\(h_θ(x) ≈ x_1 AND x_2\)

那么同理，下图的神经网络最终可以生成一个类似于OR函数的假设函数。

下图的神经网络最终可以生成一个类似于NOT函数的假设函数。

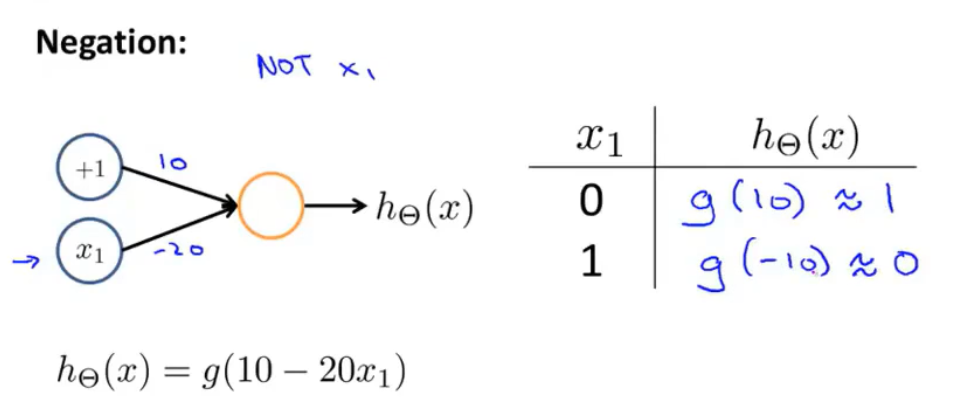
可以发现NOT是通过给对应的单元施加一个较大的负数来实现的。

非线性逻辑函数的实现

下面尝试生成如下的函数：
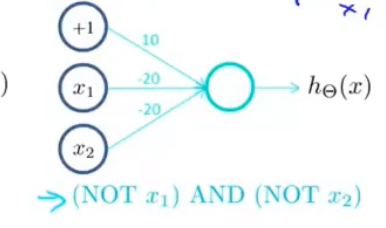
\[h_θ(x)=(NOT x_1)AND(NOT x_2)\] 分析：
要想使\(h_θ(x)=1\),那么当且仅当\(x_1=x_2=0\)时成立，最终的神经网络如下图所示：

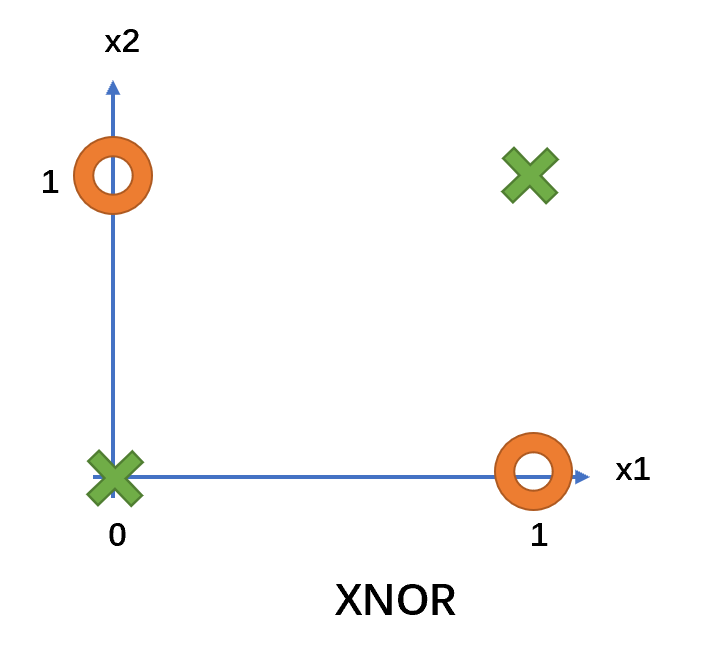
思考下面一个例子： 假设函数可以写成： \[y=x_1 XNOR x_2\] 那么神经网络是否可以生成这样的函数呢？ XNOR的四个样本分布在样本空间内的表示如下：

如果将之前的AND和OR也在样本空间中表示出来：

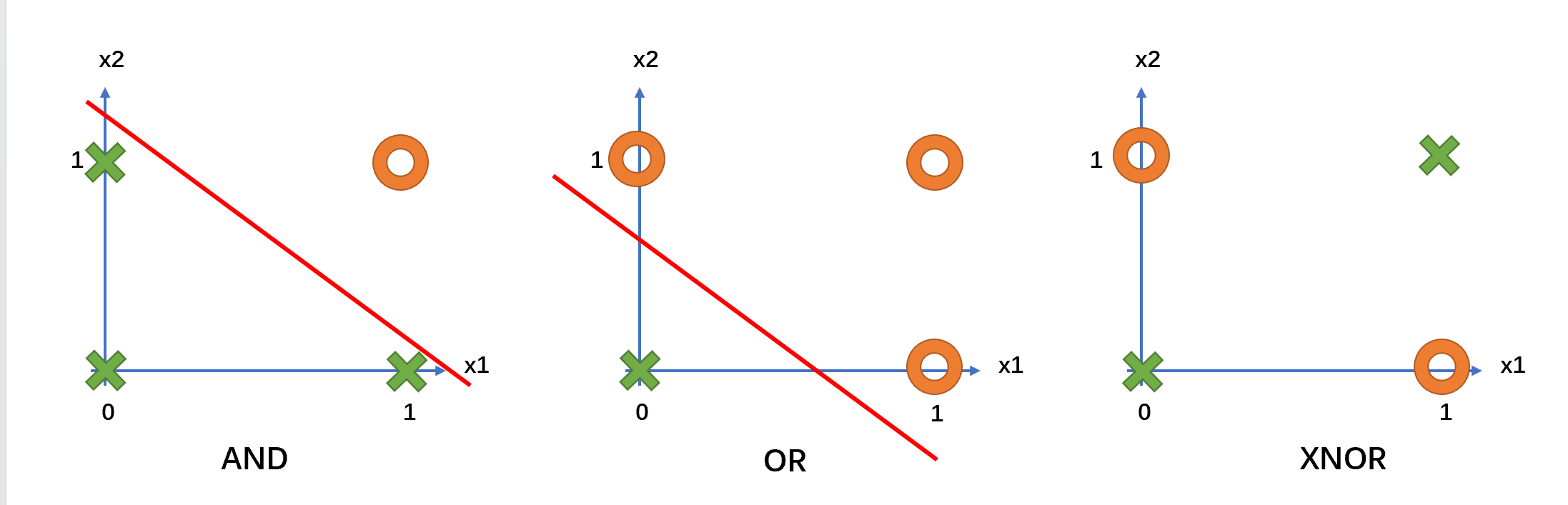
与之前不同的是，可以发现AND和OR在样本空间中的表示都可以用一条直线对其进行划分，而对XNOR无法找到一条直线将其进行区分。对于感知机而言，由于其输出表示为多个神经元的线性组合通过Sigmoid函数，只能找到数据的线性边界。 对于这样的非线性逻辑函数，需要添加多层神经元场才能完成逻辑函数的功能。具体理由如下：

分析： \[x_1XNORx_2=NOT(X_1 XOR X_2)=(x_1 AND x_2)OR((NOT x_1) AND (NOT x_2))\] 以逻辑表达式形式书写： \[h_θ(x)=(x_1.x_2)+\overline{x_1}.\overline{x_2}\] 将它分层：
第一层： 获取\(x_1\)和\(x_2\)
第二层：计算 \(a_1^{(2)}=x_1.x_2\) 和 \(a_2^{(2)}=\overline{x_1}.\overline{x_2}\).
第三层：计算 \(a_1^{(2)}+a_2^{(2)}\).
通过这一节的前半部分，我们已经知道了每一层所需要的函数的神经网络构建方法，最终的神经网络将是：

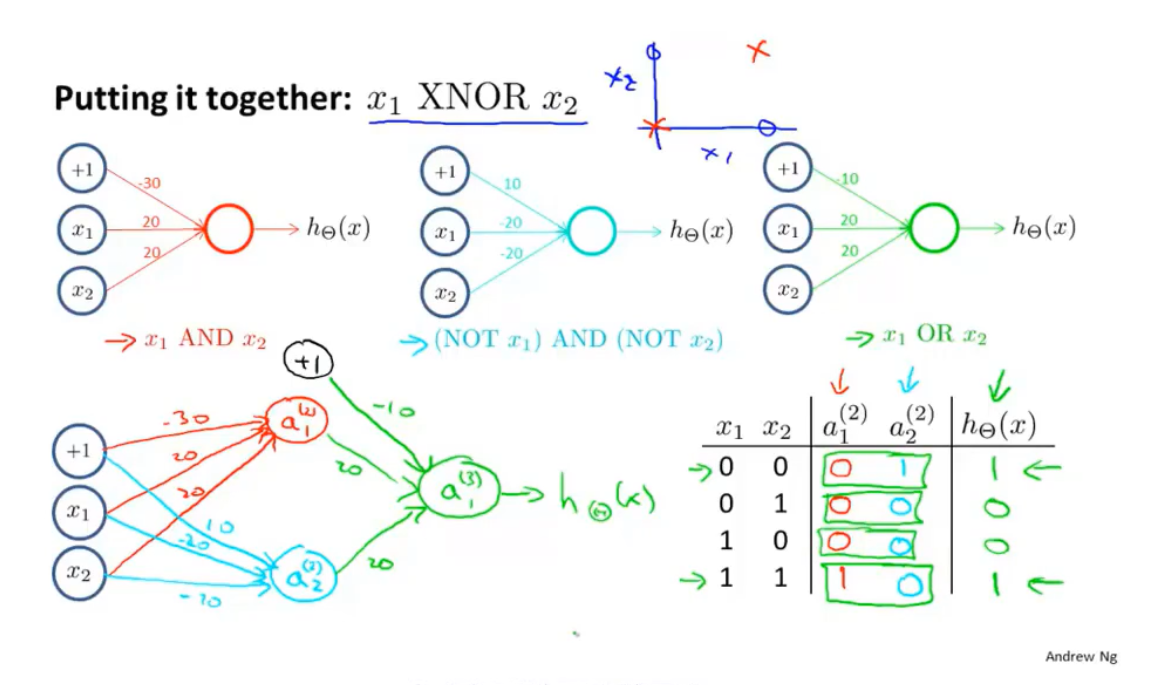
按这种方法，可以通过增加神经网络的层数和神经元的个数逐渐构造出越来越复杂的函数，也能就可以提取到更加多样化的特征，处理决策边界更复杂、非线性的数据集。
>实例： 可视化Minst手写字符数据集识别