5.5. 神经网络的代价函数·反向传播

代价函数·反向传播

回顾

接下来的讲义主要考虑两种分类问题：第一种是二元分类，如之前的讲义所述，y的取值只能是0或者1，输出层只有一个输出单元，假设函数的输出值是一个实数；第二种是多元分类，y的取值是一个k维的向量，输出层有k个输出单元。 ## 神经网络的代价函数形式 假设一个神经网络训练集有m个训练样本：\({(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}\)
\(L\)表示神经网络的总层数，\(s_l\)表示\(l\)层中神经元的数量（不包括偏置神经元）。
在神经网络中使用的代价函数是在逻辑回归中使用的正则化代价函数：
\[J(θ)=-\frac{1}{m}[∑_{i=1}^m y^{(i)} log⁡(h_θ(x^{(i)} ))+(1−y^{(i)}) log(1−h_θ (x^{(i)}))]+\frac{λ}{2m}∑_{j=1}^n θ_j^2\] 略微不同的是，在神经网络中分类标签和假设函数的输出值都变成了k维的向量，因此神经网络中的代价函数变成了：
\[J(θ)=-\frac{1}{m}[∑_{i=1}^m ∑_{k=1}^Ky_k^{(i)} log⁡(h_θ(x^{(i)} )_k)+(1−y_k^{(i)}) log(1−h_θ (x^{(i)})_k)]+\frac{λ}{2m}∑_{l=1}^{L-1}∑_{j=1}^{s_l}∑_{j=1}^{s_l+1} (Θ_{ji}^{(l)})_j^2\]
解释：
1. 用\((h_Θ(x))_i\)来表示第i个输出
2. 这个代价函数中\(∑_{k=1}^K\)表示所有的输出单元之和，这里主要是将\(y_k\)的值与\((h_Θ(x))_k\)的大小作比较
3. 正则项的作用是去除那些对应于偏置单元的项，具体而言就是不对\(i=0\)的项进行求和和正则化。

代价函数最小化：反向传播算法

过程

同之前的线性回归和逻辑回归一样，接下来要求得代价函数的最小值\(J(Θ)min\)并求出\(Θ\)。主要的步骤是写出\(J(Θ)\)并求关于每一个\(Θ_{ij}^{(l)}\)的偏导项\(\frac{∂}{∂Θ_{ij}^{(l)}}J(Θ)\)。

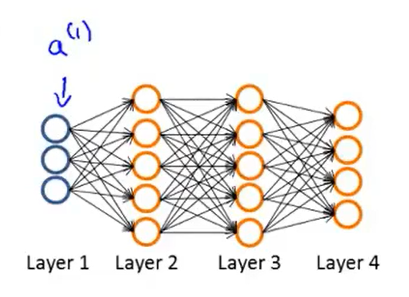
现在先来讨论如上图所示的神经网络中，只有一个训练样本\((x,y)\)的情况：
首先先用前向传播算法（见讲义4.2）验证假设函数是否会真的输出结果:
\[a^{(1)}=x\]
\[z^{(2)}=Θ^{(1)}a^{(1)},并增加一个偏置单元\]
\[a^{(2)}=g(z^{2})\] \[z^{(3)}=Θ^{(2)}a^{(2)},并增加一个偏置单元\]
\[a^{(3)}=g(z^{3})\]
\[z^{(4)}=Θ^{(3)}a^{(3)}\]
\[a^{(4)}=g(z^{4})=h_Θ(x)\]
接下来，为了计算关于每一个\(Θ_{ij}^{(l)}\)的偏导项\(\frac{∂}{∂Θ_{ij}^{(l)}}J(Θ)\)，就要用到反向传播算法（Backpropagation）。
从直观上说，对于每一个节点，都要计算每个节点的误差：\(δ^{(l)}_j\),表示第\(l\)层第\(j\)个节点的误差。
\[δ^{(l)}_j=a_j^{(l)}-y_j=(h_Θ(x))_j-y_j\]
\(y_j\)表示训练集中\(y\)向量里的第\(j\)个元素的值。
其向量形式：
\[δ^{(l)}=a^{(l)}-y\] 这里的\(δ^{(l)}\)和\(a^{(l)}\)都是一层每一个误差/输出所构成的向量。
具体而言，对于上图所示的4层（\(L=4\)）神经网络,第四层的误差项：
\[δ^{(4)}=a^{(4)}-y\] 照例写出前面两层的误差：
\[\delta^{(3)}=(Θ^{(3)})^Tδ^{(4)}⋅g'(z^{(3)})\] \[\delta^{(2)}=(Θ^{(2)})^Tδ^{(3)}⋅g'(z^{(2)})\] 事实上应用微积分的链式法则，\(g'(z^{(3)})=a^{(3)}⋅(1-a^{(3)})\),1是一个每项都为1的向量。
反向传播的步骤相当于是从最后一层开始求误差，然后将最后一层的误差传给前一层，反向依次传播。
最终将会有： \[\frac{∂}{∂Θ_{ij}^{(l)}}J(Θ)=a^{(l)}_iδ^{(l+1)}_i\] 此处忽略了正则化项：\(λ\)。
现在将反向传播算法从一个训练样本拓展到一个有m个训练样本：\({(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),...,(x^{(m)},y^{(m)})}\),\(L\)层的神经网络训练集：

定义\(Δ_{ij}^{(l)}=0\)用于计算\(\frac{∂}{∂Θ_{ij}^{(l)}}J(Θ)\),接下来遍历整个训练集：
For \(i=1\) to \(m\):
set \(a^{(1)}=x^{(i)}\) #用于将所有的x输入到输入层的激活函数中
用正向传播算法计算\(a^{(l)}~for~l=2,3,...,L\)
\(δ^{(L)}=a^{(L)}-y^{i}\) #计算最后一层的误差
用反向传播算法计算\(\delta^{(L-1)}\)到\(δ^{(2)}\),
\(Δ^{(l)}_{ij}:=Δ^{(l)}_{ij}+a_j^{(l)}δ^{(l+1)}_i\)
(写成向量的形式：\(Δ^{(l)}:=Δ^{(l)}+δ^{(l+1)}(a_j^{(l)})^T\))
结束循环后，令
\[ D^{(l)}_{ij}:=\begin{cases} \frac{1}{m}Δ^{(l)}_{ij},j=0 \frac{1}{m}Δ^{(l)}_{ij}+λΘ^{(l)}_{ij},j \not=0 \end{cases} \]
那么最终：
\[\frac{∂}{∂Θ_{ij}^{(l)}}J(Θ)=D^{(l)}_{ij}\]

理解

回顾：前向传播模型

前向传播的整个过程可以用下图表示：

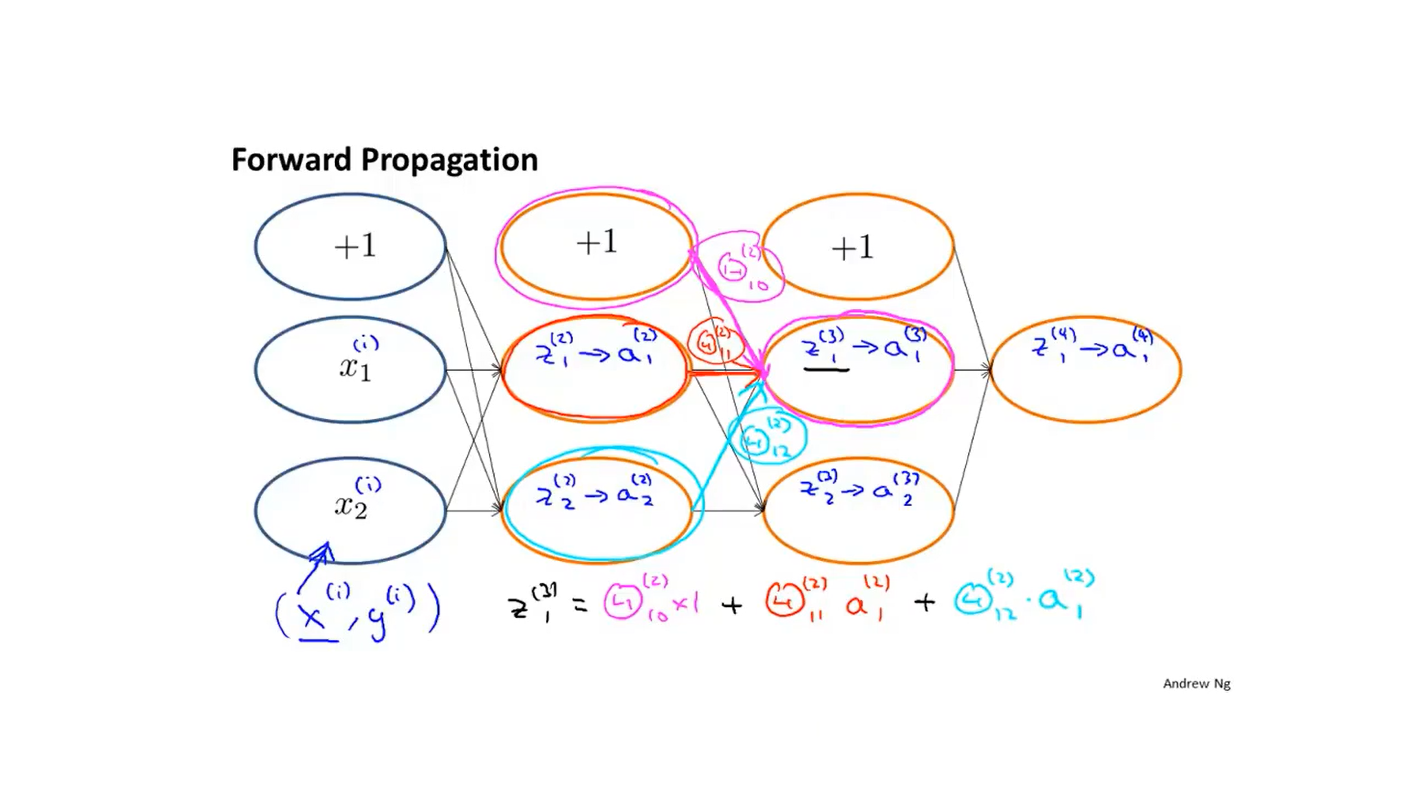
比如：如果洋红色的部分其权重为\(Θ_{10}^{(2)}\),红色的权重值为\(Θ_{11}^{(2)}\)，青色的权重值是\(Θ_{12}^{(2)}\)， 那么\(z_1^{(3)}=Θ_{10}^{(2)} \times 1+Θ_{11}^{(2)} × a_1^{(2)}+Θ_{12}^{(2)}×a_1^{(2)}\)。
反向传播的过程和前向传播非常类似，只是传播的方向不同。
#### 反向传播的理解
关注反向传播的代价函数：
\[J(θ)=-\frac{1}{m}[∑_{i=1}^m ∑_{k=1}^Ky_k^{(i)} log⁡(h_θ(x^{(i)} )_k)+(1−y_k^{(i)}) log(1−h_θ (x^{(i)})_k)]+\frac{λ}{2m}∑_{l=1}^{L-1}∑_{j=1}^{s_l}∑_{j=1}^{s_l+1} (Θ_{ji}^{(l)})_j^2\]
对于单个的样本:\((x^{(i)},y^{(i)})\)，只有一个输出单元并且忽略正则化，那么这个样本的代价函数：
\[Cost(i)=y^{(i)} log⁡(h_θ(x^{(i)} ))+(1−y^{(i)}) log(1−h_θ (x^{(i)}))\]
这个代价函数的功能类似于计算方差，可以近似的看做是方差函数：
\[Cost(i)≈(h_\Theta(x^{(i)})-y^{(i)})^2\] 它反应了样本模型输出值和样本值的接近程度。
反向传播中每个节点的误差：\(δ^{(l)}_j\),表示第\(l\)层第\(j\)个节点的误差。有：
\[δ^{(l)}_j=\frac{\partial}{∂z_j^{(l)}}Cost(i)\] \(z_j^{(l)}\)与\(h_\Theta(x^{(i)})\)相关。

反向传播的整个过程可以用下图表示：

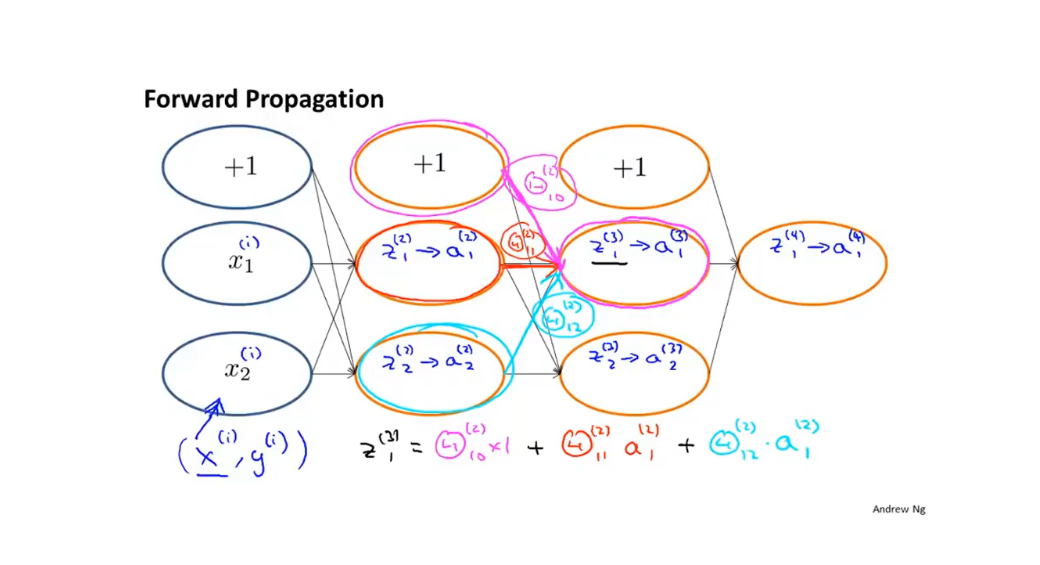
例如对\(δ^{(2)}_2\)，洋红色和红色箭头分别表示两个权重值\(Θ_{12}^{(2)}\)和\(Θ_{22}^{(2)}\)，有:
\[δ^{(2)}_2=Θ_{12}^{(2)} ×δ^{(3)}_1 +Θ_{22}^{(2)} ×δ^{(3)}_2\]