5.6. 回顾：神经网络的实现与梯度下降算法

回顾：神经网络的实现与梯度下降算法

搭建神经网络

选择神经网络的架构

即选择神经元之间的连接模式，和神经网络的层数，每一层的单元数。
- 输出和输入单元
输入单元的数目由分类问题中要区分的类别个数，即特征的维度数量所确定。
注意：多元分类问题中输出单元应该是一个多维的向量，对应的维度为1。 - 隐含层
通常只有一层隐含层；如果选择构建多个隐含层，通常情况下每一个隐含层中的单元数都是相同的。
单元数越多越好，但是隐藏单元数的增加会导致计算量的增大。因此每一个隐含层中隐藏单元的数目通常与输入层的维度，即特征的数目相匹配（是特征数目的整数倍\(k=1,2,3...\)）。

训练神经网络

1. 随机初始化权重，通常初始化为接近于0的值。
2. 执行前向传播算法，得到\(h_θ(x^{(i)})\)的值。
3. 计算代价/损失函数\(J(Θ)\)。
4. 执行方向传播算法来计算\(\frac{∂}{∂Θ_{jk}^{(l)}}J(Θ)\)具体执行方法是用一个循环for i = 1:m对每一个样本执行前向传播和反向传播算法，得到每一个单元的激励值\(a^{(l)}\)和误差\(δ^{(l)}\)。
5. 使用梯度检查，将反向传播算法得到的\(\frac{∂}{∂Θ_{jk}^{(l)}}J(Θ)\)与用数值近似得到的\(J(Θ)\)的梯度进行比较，确定两个值是接近的。
6. 停用梯度检查。
   
7. 用梯度下降算法或者其他的一些高级的优化方法与反向传播算法结合，并最小化\(J(Θ)\)的\(Θ\)。

梯度下降算法在神经网络中的应用

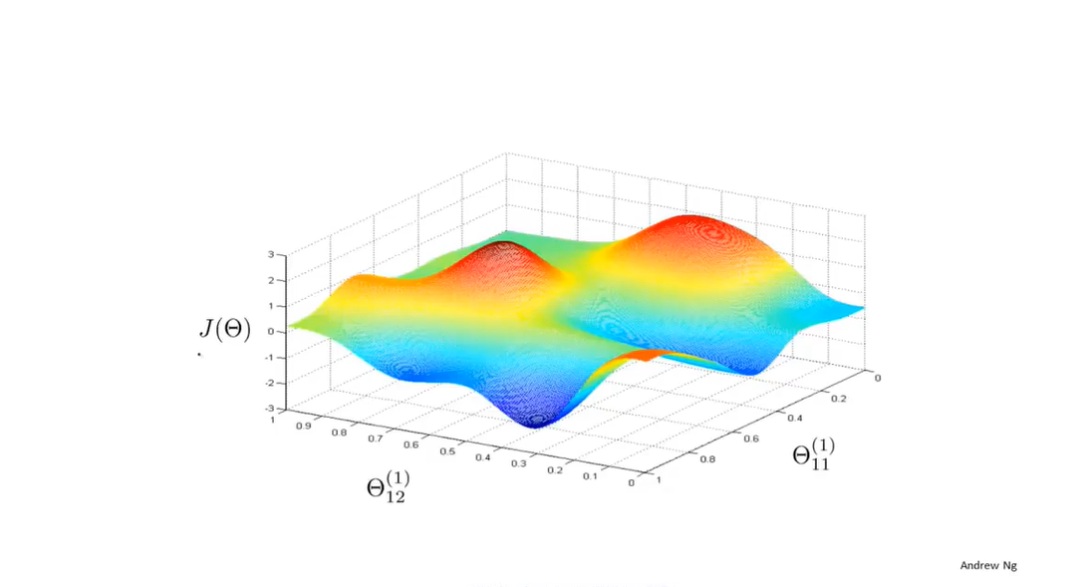
如图所示的参数与\(J(Θ)\)的关系中（图中只有两个参数），图中每一点的高度表示了\(J(Θ)\)的值，也代表了在该点的参数取值下，预测值\(h_Θ(x^{(i)})\)与实际标签\(y^{(i)}\)的差距。
同之前一样，梯度下降算法从随机的一点开始求这一点的梯度（即下降的最快方向），然后沿着梯度方向持续下降，直到得到局部最优点。

案例： ALVINN无人驾驶转向

Dean Pomerieau使用三层神经网络ALVINN来训练计算机进行无人驾驶。
将汽车转向进行量化，左急转和右急转分别对应了坐标轴上仅有的两个极值点。 每隔两秒，ALVINN就会生成一张前方的路况图，并记录驾驶者的行驶方向，在最开始ALVINN的转向是随机的，通过训练路况图和行驶方向的关系，ALVINN最终做出的转向决定与人类驾驶员的转向基本相同。