02. 系统概述

系统概述

系统的类型

系统可以用数学模型和框图来表示。
系统\(H[·]\)的基本数学模型是:
\[y(⋅)=H[f(⋅)]\] 称\(y(⋅)\)是系统的输出，\(f(⋅)\)是系统的输入。 因此对输入的处理与系统本身无任何关系。
按照系统的数学模型类型，系统可以分为即时系统（输出（称为系统的响应）仅与当前的输入（称为系统的激励）有关）和动态系统（响应与过去和现在的激励都有关系），离散系统（激励和响应都是离散信号）和连续系统（激励和响应都是连续信号）。

本课程主要讨论动态系统。
## 系统的框图模型
表示系统基本功能的常用单元有：积分器（连续）/延迟单元（离散），加法器，数乘器，延时器。
它们的框图如下图（《信号与线性系统分析》）所示。

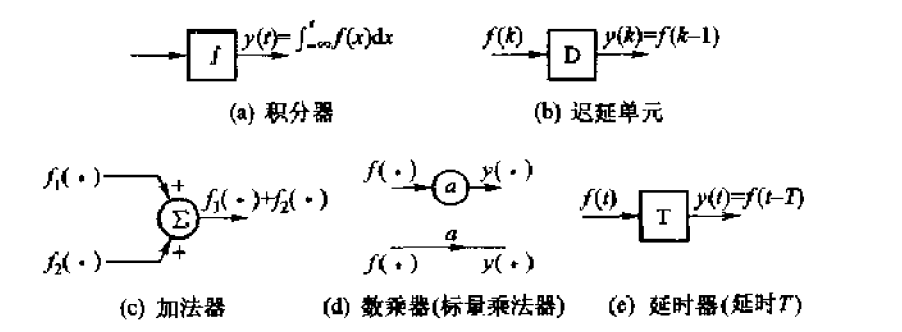
通常的系统方程是左边为系统的输出结果，右边为系统的输入结果。
给定已知框图，写出对应的方程的流程通常是：
1. 找到系统中的数个加法器，通过分析加法器的来源信号列出等式。
2. 将等式进行处理，最终得到\(f(t)\)与\(y(t)\)的方程。

线性时不变系统的特性

线性

线性包含两个内容： 齐次性和可加性。
若系统满足：
\[H[af(·)]=aH[f(·)]\]
称系统\(H(·)\)具有齐次性。
若系统满足：
\[H[f_1(·)+f_2(·)]=H[f_1(·)]+H[f_2(·)]\] 称系统\(H(·)\)具有可加性。
若以上两点系统\(H(·)\)都满足，即： \[H[C_1f_1(·)+C_2f_2(·)]=C_1H[f_1(t)]+C_2H[f_2(t)]\] 称系统是线性的。
动态系统的线性判别
动态系统的响应\(y(·)\)与初始状态\(x(0)\)和系统激励\(f(·)\)相关，称输入信号为0（\(f(t)=0\)）时，仅有初始状态引起的响应叫零输入响应\(y_{zi}\)； 初始状态为0（\(x(0)=0\)）时，仅由输入信号引起的响应叫零状态响应\(y_{zs}\)。线性系统的全响应可以分解为这两种响应，称为线性系统的分解特性。
如果系统有多个初始状态或/和多个输入信号，对于每一个输入的零状态响应和对于每一个零输入响应都呈现线性，称为零状态/零输入线性。
如果一个系统具有分解特性、零状态/零输入线性特性，则该系统是线性系统。 因此求解一个动态系统是否是线性系统的步骤：
1. 判断系统的零状态响应和零输入响应，将其相加判断是否满足分解性。
2. 令\(f_3(t)=f_1(t)+f_2(t)\)，带入零状态响应和零输入响应，看两者是否分别满足线性。

时不变性

如果系统的参数都是不随着时间变化的常数，称这样的系统是时不变系统。
判断方法：系统的输出与激励时移的时间无关，即：
\[y(t-τ)=H[f(t-τ)],y(t)=H[f(t)]\]
动态系统的时不变性判别
1. 找出系统的零状态。
2. 带入\(f(t-τ)\)，看系统结果是否是\(y(t-τ)\)。

因果性

如果视激励为响应产生的原因，零状态响应是激励的结果，那么响应不应该出现于激励之前。 换句话说，系统的响应不应该与未来的激励有关，而只与现在和过去的激励有关。
称这样的系统为因果系统，因果系统只在以时间为变量的系统中出现。
对于系统输出\(y(t_r)\),如果系统输入\(x(t_i)\)导致\(t_i>t_r\)，此时系统的因果性被破坏，系统不具有因果性。

稳定性

如果系统的激励是有界的，且零状态响应也是有界的，称这样的系统是稳定系统。

LTI系统分析方法概述

描述系统的方法

• 输入-输出法
  只把输入变量和输出变量作为描述的因素，系统内部的结构视作黑箱。
  
• 状态变量法
  状态变量法用两个方程描述系统：
  1. 状态方程：描述系统内部状态与输入的关系。
     
  2. 输出方程： 描述系统内部响应与输入和状态变量之间的关系。

求解系统方程的方法

• 时域分析法
  直接分析时间变量函数。连续系统通常由微分方程描述，离散系统通常由差分方程描述。因此直接求解对应的以时间为变量的方程。此外还有卷积方法。
  
• 变换法
  对时间变量函数转换为某个域中以其他因素作为变量的函数。