01. 信号概述

信号概述

按照时间特性的信号分类

确定信号和随机信号

1. 确定信号
   除了间断点外，对于一个确定的时间\(t\),都能有一个确定的值\(f(t)\)与之对应。
   
2. 随机信号
   又分为稳定的和不稳定的随机信号。
   
3. 伪随机信号

连续时间信号和离散时间信号

1. 连续时间信号
   除了间断点外，在任何时间\(t\)都能找到一个与之对应的值\(f(t)\)。
   连续时间信号的值域可以是连续的，也可以是不连续的。 例如模拟信号：x轴连续，y轴也连续（可以取到任意值）。

2. 离散时间信号
   只有在离散的点\(n\)上存在对应的值\(x(n)\)。
   离散时间信号的定义域是离散的，对值域不做定义。
   数字信号是一种x轴离散，y轴离散的信号。
   均匀的离散信号通常称为序列。

模拟信号和数字信号的转换：
模拟信号经过取样使得x轴离散后，在通过量化使得y轴也离散，进而得到数字信号。

周期信号和非周期信号

周期信号是在实数域每隔一定时间T/或者整数N，按规律重复变化的信号。
\[f(t)=f(t+mT),m ∈Z\] \[x(n)=x(n+mN),m ∈Z\]

常见的时间连续信号

• 指数信号
  
• 正弦信号
  衰减的正弦信号： \[f(t)=ke^{-at}sinωt \text{ t>=0}\]
  
• 复指数信号
  
• 采样信号
  \[sinc(x)=\frac{sinx}{x}\]
  
• 奇异信号
  • 单位阶跃信号
    \[u(t)=\begin{cases} 0 ~t<0\\ 1 ~t>0\\ \end{cases}\] 注意: 当\(t=0\)时，定义\(u(0)=0.5\)（《信号与线性系统分析》）。
    变化：
    左移的阶梯信号： \(u(t+t_0)=\begin{cases} 0 ~t<0\\ 1 ~t>0\\ \end{cases}\)
    右移的阶梯信号：\(u(t-t_0)=\begin{cases} 0 ~t<0\\ 1 ~t>0\\ \end{cases}\)
    门信号：\(g(t)=u(t+\frac{\tau}{2})-u(t-\frac{\tau}{2})\)
    符号函数： \(sig(t)=2u(t)-1\)
    
  • 单位冲激函数和冲击偶函数
    推导：
    面积为1，宽为\(τ\)，高为\(\frac{1}{τ}\)的门函数，其对称轴是\(x=0\)。
    令\(τ→0\),得到宽为\(0\)，高为\(∞\)的单位冲激函数\(δ(t)\)，即：
    \[δ(t)=lim_{τ→0}\frac{1}{τ}[u(t+\frac{τ}{2})-u(t-\frac{τ}{2})]\]
    有：
    \[u'(t)=δ(t)\]
    任意的信号都可以被分解为有权的单位冲激信号。 冲激函数的表示：
    
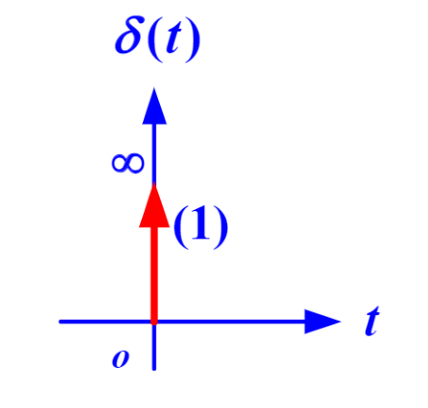
    如上图，其中\((n)\)表示强度为\(n\)的冲激函数，即\(nδ(t)\)。
    性质：
    1. 赋值性
       \[∫δ(t)f(t)dt=f(0)\]
    2. 偶函数
       \[δ(t)=δ(-t)\]
    3. 缩放 \[δ(at)=\frac{1}{|a|}δ(t)\] 证明思路都是利用函数相等=积分相等，分情况讨论得到。
       对单位冲激函数求导，得到冲击偶函数，即\(δ'(t)\)。
       性质：
       
    4. 赋值性
       \[∫δ'(t)f(t)dt=-f'(0)\]
       \[f(t)δ'(t)=f(0)δ'(t)-f'(0)δ(t)\]
    5. 奇函数
       \[δ'(t)=-δ'(t)\]

常见的时间离散信号

• 单位采样信号
  \[δ(n)=\begin{cases} 0,n\not ={0} \\ 1, n=0 \\ \end{cases}\] 任何的非连续信号都能够用单位采样信号表示。
  
• 单位阶梯信号
  \[u(n)=\begin{cases} 0,n≧{0} \\ 1, n<0 \\ \end{cases}\] \(δ(n)\)是\(u(n)\)的差分信号。
  \[δ(n)=u(n)-u(n-1)\]
  
• 方波序列
  
• 斜坡序列
  
• 单边指数序列
• 正弦序列
  正弦函数到正弦序列的转换：
  令\(t=nT_s\)， 有\(f(t)=sin(ω_0t)=sin(ω_0T_sn)=x(n)\)
  令\(Ω_0=ω_0T_s\)，得到：
  \[x(n)=sin(Ωn)\]
  注意：
  1. \(T_s\)表示的是采样的间隔时间，周期\(T=nT_s\)。
     
  2. 对于周期序列，有\(x(n)=x(n+N)\)。
  3. 如果\(\frac{2π}{Ω}\)不为有理数，那么正选序列不具有周期。

信号的基本处理

加法和乘法

• 对于连续信号 函数直接相加或者是相乘。
  注意： 两个周期连续信号相加不一定是一个周期信号
  

• 对于离散信号 两个序列的对应位置相加或者是相乘。
  ### 积分和微分
  

• 对于连续信号 先做信号分解，对每一段分别积分或者微分。

• 对于离散信号 只有累积（\(z(n)=∑x(k)\)）和差分（\(Δx(n)=x(n+1)-x(n)\)或\(Δx(n)=x(n)-x(n-1)\)）。 ### 平移、反转和尺度变换 平移遵循左加右减的原则。
  横坐标展缩遵循a>1,图像压缩，a<1，图像扩展的原则。
  由于离散信号\(x(an)\)当且仅当\(ak\)是一个整数的时候才有定义，如果对其进行展缩，通常会丢失原信号\(x(n)\)的部分信息，因此离散信号通常不做展缩。
  

• 作图方法
  一种方法是将信号每一段的分段函数都求出，并将\(at+b\)代入分段函数及其范围，得到新的函数图像。
  已知\(f(t)\),求\(f(at+b)\)的图像：基本思路是令\(τ=at+b\)，反解出\(t\)的方程，从图像上选择几个关键点，将图像上这些点原来\(t\)轴的值到\(τ\)中，得到新的\(t\)值。
  已知\(f(at+b)\),求\(f(t)\)的图像： 基本思路是从图像选择几个关键点，将图像上这些点原来\(t\)轴的值到\(τ\)中，得到新的\(t\)值。

信号分解

• 奇偶分解 \[\begin{aligned} f(t)=f_e(t)+f_o(t) \\ f_e(t)=\frac{1}{2}[f(t)+f(-t)]\\ f_o(t)=\frac{1}{2}[f(t)-f(-t)] \end{aligned} \]
• 复分解
  \[f(t)=f_r(t)+jf_i(t)\]
• 直流交流分解
  \[f(t)=f_A(t)+f_D(t)\] \[f_D(t)=\frac{1}{T}∫^{t_0+T}_{t_0}f(t)dt\]