04. 频谱·非周期信号的傅里叶变换

频谱·非周期信号的傅里叶变换

信号的频谱

已经知道信号可以分解为一系列正弦信号或者是数字数信号的和。
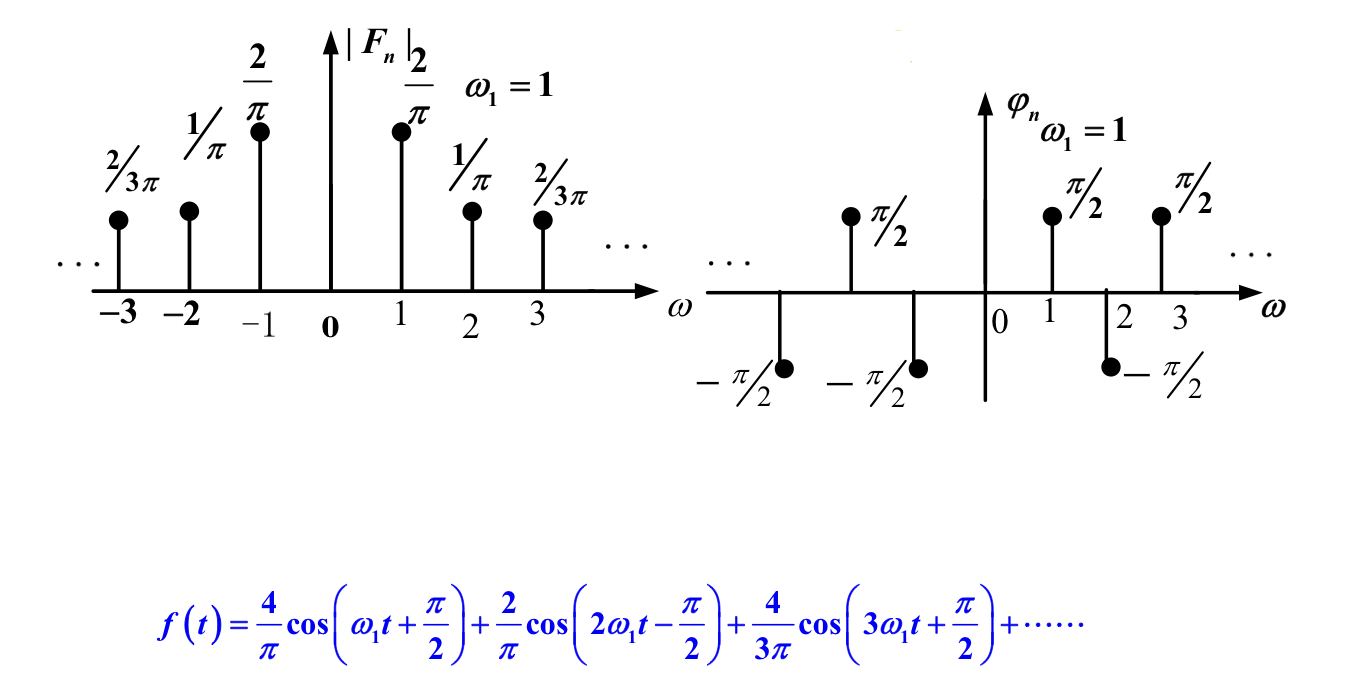
以各分量（称为各谐波（Harmonics））对应的角频率为横坐标，以各分量的幅值或者是相位为纵坐标绘制图像，就能得到信号的频谱图像。
频谱分为两种，单边频谱（描述三角形式的傅里叶级数）和双边频谱（描述指数形式的傅里叶级数）。
要绘制其单边或双边的幅值频谱和相位频谱，才能够完整地描述一个傅里叶级数。
单边频谱和双边频谱的关系：
单边频谱的幅值是双边频谱的两倍：\(A_{uni}=2A_{bil}=√{a_n^2+b_n^2}\)。
两者相位相同：\(ϕ_n=arctan(-\frac{b_n}{a_n})\)。
例如下图中的三角形式傅里叶级数，可以用单边频谱表示后转换为图中的双边频谱。

周期矩形脉冲信号的频谱

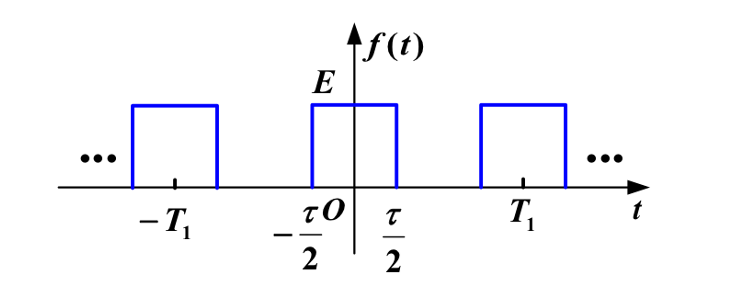
对上图的周期脉冲信号求其傅里叶系数，得到：
\[F(nω)=\frac{Eτ}{T_1}Sa(nω_1\frac{τ}{2})\]

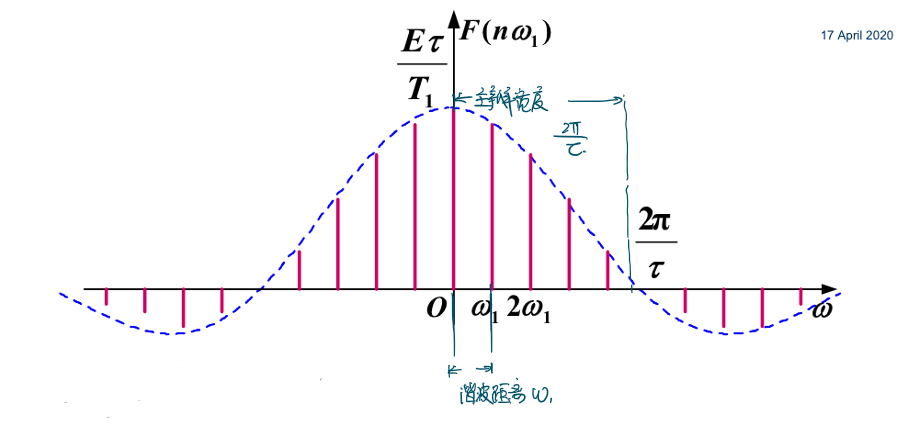
称相邻两个分量间的距离为谐波距离，谐波距离为\(ω_1\)，函数与横轴的第一个交点为主瓣宽度：\(\frac{2\pi}{\tau}\)。
定义\(ω_1=\frac{2π}{T_1}\),\(T_1\)为采样周期。 可以发现主瓣宽度不变的前提下，\(T_1\)越大，谐波距离越小，谐波分布越稠密。当\(T_1→∞\)时，整个频谱将趋于连续。
因此周期信号的频谱是离散的，非周期信号的频谱是连续的。 - 周期信号的功率
归一化（R=1\(Ω\)）的周期信号的平均功率可以由如下的公式表示：
\[P=\frac{1}{T}∫_0^Tf(t)dt=∑F(nω_1)^2\]

傅里叶变换、反变换的推导

对指数形式的傅里叶系数参数：
\[F(nω_1)=\frac{1}{T}∫_0^Tf(t)e^{-jnω_1t}dt\] 两边同时乘上周期：
\[TF(nω_1)=∫_0^Tf(t)e^{-jnω_1t}dt\] 当\(T→∞\)时，左边\(TF(nω_1)\)是一个有界函数，此时频谱连续\(nω_1→ω\)，定义频谱密度\(F(ω)\)：
\[\begin{aligned} F(ω) &=lim_{T→∞}TF(nω_1)\\ &=lim_{T→∞}∫_0^Tf(t)e^{-jnω_1t}dt\\ &=∫f(t)e^{-jnω_1t}dt \end{aligned}\] 定义傅里叶变换算子\(F[⋅]\):
\[F[⋅]=∫⋅e^{-jω_1t}dt\] 可得傅里叶变换：
\[F[f(t)]=∫f(t)e^{-jω_1t}dt\]
变换后的结果一定可以表示为复指数形式：
\[F(ω)=|F(ω)|e^{jϕ(ω)}\]
称\(|F(ω)|\)为振幅，\(ϕ(ω)\)为相位角。
对傅里叶变换的指数形式变形：
\[\begin{aligned} f(t)& =∑F(ω_1)e^{jω_1t}\\ &=∑\frac{F(ω_1)}{ω_1}ω_1e^{jω_1t} \end{aligned} \] 当\(T→∞\)时，可证明\(\lim_{T→∞}\frac{F(nω_1)}{ω_1}=\frac{F(ω)}{2π}\)，有：
\[f(t)=\frac{1}{2π}∫F(ω)e^{jωt}dω\] 将如上式子定义为傅里叶反变换。
因此：
傅里叶变换：\(F[f(t)]=∫f(t)e^{-jnω_1t}dt\)
傅里叶反变换：\(f(t)=\frac{1}{2π}∫F(ω)e^{jωt}dω\)
此外应用奇偶分解和欧拉公式可以将傅里叶变换分解为：
\[F(ω)=2∫f_e(t)cosωtdt-2j∫f_0(t)sinωtdt\]

傅里叶变换的性质

1. \(f(-t)→F(-ω)\)
2. \(f(-t)→F^*(ω)\)
3. 线性
4. 对偶性： \(F(t)→2πf(-ω)\)
5. 变换操作：
   • 尺度变换：\(f(at)→\frac{1}{|a|}F(\frac{ω}{a})\)
   • 时移： \(f(t-t_0)→F(ω)e^{-jωt_0}\)
   • 综合：\(f(at+b)=f(a(t+b/a))→\frac{1}{|a|}F(\frac{ω}{a})e^{-jω\frac{b}{a}}\)
     
   • 频移：\(F(ω+ω_0)→f(t)e^{-jω_0t}\)
     
6. 导数：
   • 时域倒数：\(f'(t)→jωF(ω)\)
     
   • 频域导数：\(F'(ω)→-jtf(t)\)
7. 积分：
   • 时域积分：\(∫f(t)dt=πF(0)δ(ω)+\frac{F(ω)}{jω}\)

总结：

常见非周期信号的傅里叶变换

方波/门函数

\[f(t)=E, -\frac{τ}{2}<t<\frac{τ}{2}\] \[G(t)=f(t)=u(t+\frac{τ}{2})-u(t-\frac{τ}{2})\] 由于\(f(t)\)只在振幅处有值，因此：
\[\begin{aligned} F(ω)=& ∫_{-\frac{τ}{2}}^{\frac{τ}{2}}Ee^{-jωt}dt \\ & =EτSan(\frac{ωτ}{2}) \end{aligned}\]
### 直流信号 \[f(t)=E\] 由于直流信号不满足狄利克雷条件中的绝对可积，因此需要考虑其他方法对其做变换。
当门函数的\(τ→∞\)时，可以将门函数视作一个直流信号函数。
\[\begin{aligned} F(ω) &=\lim_{τ→∞}∫^τ_{-τ}Ee^{-jωt}dt \\ &= E\lim_{τ→∞}\frac{2sin(ωτ)}{ω} \\ &=2πEδ(ω) \end{aligned}\]
当\(E=1\)时，可以推导出 \[F(ω)=2πδ(ω)\]
### 单位冲激函数
\[F(ω)=∫δ(t)e^{-jωt}dt=1\]
### 单位冲击偶函数
\[F(ω)=∫δ'(t)e^{-jωt}dt=jω\] ### 单侧指数函数
\[f(t)=Ee^{-αt}u(t)\]
\[\begin{aligned} F(ω)=& ∫Ee^{-αt}u(t)dt \\ & =∫_0^∞Ee^{-αt}dt \\ & =\frac{E}{α+jω} \end{aligned}\]
对其做复指数变换，就能得到其振幅和相位角：
\[\begin{aligned} F(ω) &=\frac{E(α-jω)}{α^2+ω^2}\\ &= \frac{E}{√(a^2+ω^2)}e^{-jarctan\frac{ω}{α}} \end{aligned}\]
### 符号函数
\[sgn(t)=\begin{cases} 1,t>0\\ -1,t<0 \end{cases}\] 由于不满足狄利克雷条件中的绝对可积（在t=0处不可积），因此需要对函数做变换，使其可积。
设\(f_1(t)=sgn(t)e^{-α|t|}\) \[\begin{aligned} F(ω)&=\lim_{α→0}[∫_{-∞}^{0}-e^{αt-jωt}dt+∫_0^{∞}e^{-αt-jωt}dt]\\ &=-\lim_{α→0}\frac{2jω}{α^2+ω^2}\\ &=\frac{2}{jω} \end{aligned}\]
复指数形式：
\[F(ω)=\frac{2}{|ω|}e^{⨦\frac{π}{2}j}\]
### 单位阶梯函数
由\(u(t)=\frac{1}{2}(1+sgn(t))\)：
$$ \[\begin{aligned} F(ω)&=∫\frac{1}{2}(1+sgn(t))e^{-jωt}dt\\ &=\frac{1}{2}[∫e^{-jωt}dt+∫sgn(t)e^{-jωt}dt\\ &=πδ(ω)+\frac{1}{jω} \end{aligned}\]

$$