05. 时域分析方法(微分/差分方程·卷积)
本文最后更新于 2025年6月4日 晚上
时域分析方法(微分/差分方程·卷积)
微分/差分方程的解
从本节开始:
名词“系统输入”与“系统激励”等同,系统输出与系统响应等同。
在定积分中\(∫\)表示从-∞到∞的积分,\(∑\)表示从-∞到∞的和。
线性时不变系统可以用一个关于激励(\(e(t)\))和响应(\(r(t)\))的\(n\)阶微分/差分方程对其描述。
\(n\)阶在电路中的具体表现为\(n\)个电容/电感。
\[C_0\frac{d^nr(t)}{dt^n}+C_1\frac{d^{n-1}r(t)}{dt^{n-1}}+...+C_nr(t)=E_0\frac{d^me(t)}{dt^m}+E_1\frac{d^{m-1}e(t)}{dt^{m-1}}+...+E_me(t)\]
这个方程的解由齐次解和特解两部分组成,齐次解与特解的和构成方程的全解。
齐次解
当输入全部为0时,得到的方程:\(C_0\frac{d^nr(t)}{dt^n}+C_1\frac{d^{n-1}r(t)}{dt^{n-1}}+...+C_nr(t)=0\),称之为特征方程。
由特征方程得到的解称为齐次解。齐次解表示系统的零输入响应。
求齐次解
将特征方程转化为多项式并求解。
对于微分方程的特征方程,其\(n\)阶微分项可以被换元为\(α^n\)项,最终将特征方程转化为关于\(α\)的\(n\)阶多项式。
对于差分方程的特征方程,其0阶差分项\(y(n)\)可以被换元为关于\(α\)的最高幂项,如此类推,最终将特征方程转化为关于\(α\)的\(n\)阶多项式。
根据多项式的解的个数和是否有重根,可以在下表中找到齐次解的形式,并带入多项式的解。
将齐次解带入已知方程的特解(通常是系统的零状态响应),利用对应阶数项系数相等,求出齐次解中的常系数。
不同特征根所对应的齐次解(微分方程)
特征根 齐次解\(y_p(t)\) 单实根 \(e^{αk}\) r重实根 \(∑C_{r-1}t^{r-1} e^{αk}\) 不同特征根所对应的齐次解(差分方程)
特征根 齐次解\(y_p(k)\) 单实根 \(Cα^k\) r重实根 \(∑C_{r-1}k^{r-1} α^k\)
特解
当激励为特定的值或者是函数时,方程的解称为特解。
求特解
- 带入具体的激励\(e(t)\)到系统的微分/差分方程。
- 通过0阶项\(r(t)\)与激励中最高次数项之间系数的关系,用待定系数法猜想系统响应\(r(t)\)的结构。
- 将\(r(t)\)的结构代回微分/差分方程,利用对应阶数项系数相等建立方程,解出\(r(t)\)结构中的常系数。
如果已知了一些特解,求另一些特解,可以使用迭代法。
即从\(h(0)\)开始列出微分方程,直到列到所求的特解对应的微分方程,将已知的特解带入,从而求出未知的特解。
卷积
零状态响应和零输入响应
在第二讲中对零状态响应和零输入响应以及线性关系进行过介绍,值得注意的是:零状态响应\(r_{zs}(t)\)和零输入响应\(r_{zi}(t)\)是相互独立的,即任何的输入只会影响到零状态响应中t的取值,而不会影响零输入响应中t的取值。
零输入响应与系统方程的通解有关,零状态响应与系统方程的特解/非齐次解有关。
两者可以通过解非齐次的微分/差分方程得到,解微分/差分方程的通用方法是卷积。
卷积方法
在连续系统中,定义\(*\) 为卷积符号,定义卷积运算:
\[g(t)=f(t)*h(t)=∫f(τ)h(t-τ)dτ\]
由于任何信号都可以被分解为\(n\)个宽为τ,高为\(f(nτ)\)的门信号,在\(τ\)非常小的时候可以认为\(gate(t)=u'(t)Δτ=δ(t)\),因此任何的信号都可以用与冲激信号的卷积来表示:
\[f(t)=∫f(τ)δ(t-τ)dτ\]
几何意义
两个信号\(f(t)\)\(h(t)\)卷积的几何意义是: 将其中一个图像左右翻转,然后从\(t=0\)处向右平移,平移过程中两个函数图像重叠面积的变化即为卷积图像。
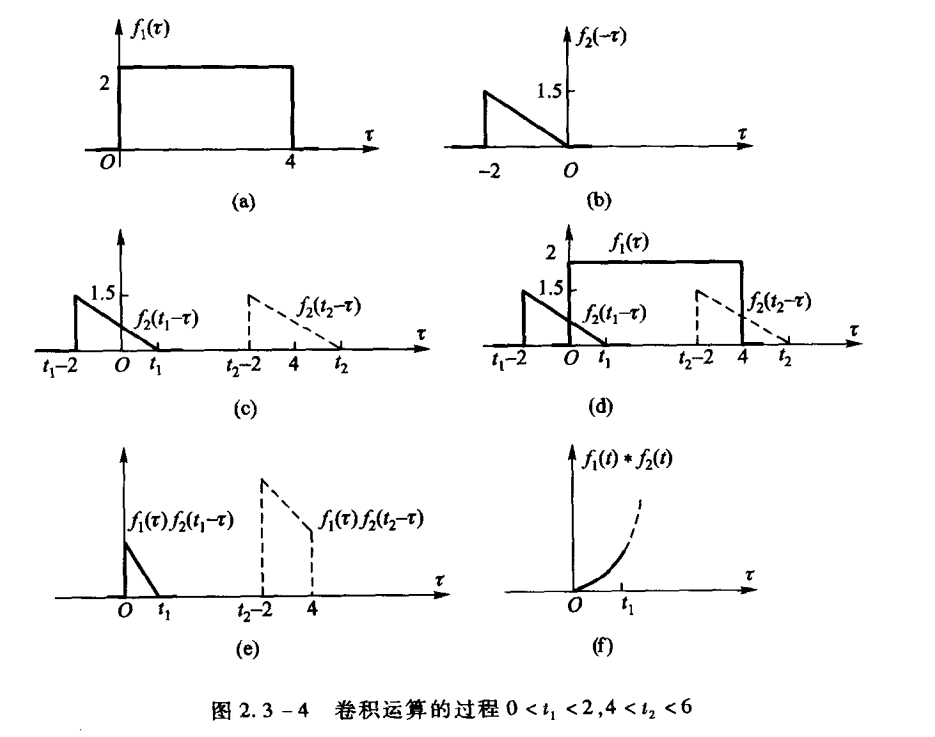
计算性质
基本性质:交换律,结合律,分配率。
微分和积分特性: \[g'(t)=f'(t)*h(t)=f(t)*h'(t)\]
\[g^{(n-m)}(t)=f^{(n)}(t)*h^{(-m)}(t)=f^{(-m)}(t)*h^{(n)}(t)\]
注:\(g^{(n-m)}(t)\)表示对\(g(t)\)作n次微分,m次积分。
与冲激函数或阶跃函数卷积
- \(f(t)*δ(t)=f(t)\)
- \(f(t-t_0)*δ(t-t_1)=f(t-t_0-t_1)\)
- \(f(t)*δ'(t)=f'(t)\)
卷积和
在离散系统中,定义卷积和: \[f(k)=∑f(i)h(k-i)\] 任何的离散序列都可以用其自身与单位序列的卷积和表示: \[f(t)=∑f(i)δ(k-i)di\]
卷积和也同样满足如上的计算性质和一些特殊的卷积结果:
\[x(k)*\delta(k)=x(k)\]
\[x(k)* δ(k-1)=x(k-1)\]
冲激响应和单位序列/取样响应
一个连续的LIT系统零状态下输入单位冲激函数\(δ(t)\),所引起的响应称为单位冲激响应,记作\(h(t)\)。 冲激响应是\(e(t)=δ(t)\)时微分方程的特解。
连续系统的零状态响应\(r_{zs}(t)\)可以表示为系统输入\(f(t)\)与单位冲击响应\(h(t)\)的卷积:
\[r_{zs}(t)=f(t)*h(t)\]
一个离散的LIT系统零状态下输入单位序列\(δ(k)\),所引起的响应称为单位取样响应,记作\(h(k)\)。 连续系统的零状态响应\(r_{zs}(k)\)可以表示为系统输入\(f(k)\)与单位冲击响应\(h(k)\)的卷积:
\[r_{zs}(k)=f(k)*h(k)\]
阶跃响应
一个LIT系统零状态下输入单位阶跃函数\(u(t)\)所引起的响应称为单位阶跃响应,记作\(g(t)\)。 由\(u(t)=∫δ(t)dt\), \[g(t)=∫_{-∞}^t h(t)dt\]
卷积积分需要满足条件\(f_1(τ)f_2(t-τ)≠0\),由于对阶跃函数\(u(t)\),\(t>0\),因此阶跃响应通从用于决定卷积积分的上下限。