09. 系统方程

系统方程

系统方程概述

对于一个有输入和输出的系统，可以通过观察系统输入和输出的关系来建立描述系统的方程，在拉普拉斯变换的s域下，系统方程可以表述为系统输出与输入之比：
\[ H(s)=\frac{R(s)}{E(s)}\] 也可以按照时域分析方法中的理解，当\(e(t)=δ(t)\)时，其拉普拉斯变换为1，因此系统方程也是输入为冲激函数时的系统输出。

类型

策动点方程

当系统是一个单口网络（One-port network，输入和输出在同一个端口的系统）时，系统方程称为策动点方程(Driving point funtion)。对于电路分析，单口网络的系统方程可以是\(H(s)=\frac{I(s)}{V(s)}\)，也可以是\(H(s)=\frac{V(s)}{I(s)}\)。

传递函数

当系统是一个两口网络时，此时的系统方程称为传递函数（Transfer function）。分析时需要找到电路的输入和输出，作比即可得到传递函数。

连接

并联

如果两个系统并联，新的系统方程为：\(h(t)=h_1(t)+h_2(t)\)，在s域内：
\[H(s)=H_1(s)+H_2(s)\]

串联/级联

如果两个系统串联，新的系统方程为：\(h(t)=h_1(t)*h_2(t)\)，在s域内：
\[H(s)=H_1(s)H_2(s)\]

举例：放大器的并联和串联

系统方程的结构

如之前提到的拉普拉斯反变换和z反变换，由于系统输入和输出在s域内都以多项式表示，系统方程自然是两个多项式的比值： \[H(s)=\frac{R(s)}{E(s)}=K\frac{Π(s-z_i)}{Π(s-p_k)}\] 其中\(p_i\)称为系统方程的极点，\(z_k\)称为系统方程的零点。
在电路分析中，极点描述的的对象是电路中电容和电感的个数，即系统方程的阶数。
同理，离散系统的方程也可以写作两个多项式的比： \[H(z)=\frac{∑b_rz^{-r}}{∑a_kz^{-k}}=A_0+∑\frac{A_kz}{z-p_k}\]

强迫响应和自由响应

如果将系统的输入\(E(s)\)以多项式表示：\(E(s)=\frac{Π(s-z_l)}{Πs-p_k}\)，系统方程\(H(s)=\frac{Π(s-z_j)}{Πs-p_i}\)，由系统的零输入响应\(R(s)=E(s)H(s)\):
\[R(s)=∑\frac{A_k}{s-p_k}+∑\frac{A_i}{s-p_i}\] 经过拉普拉斯反变换：
\[r(t)=∑A_ke^{p_kt}u(t)+∑A_ie^{p_it}u(t)\] 可以发现\(r(t)\)受到两部分的影响：系统方程和输入信号：称\(r(t)\)受输入影响的部分为强迫响应，受系统方程影响的部分为自由响应。

瞬态响应和稳态响应

分析时域中的\(r(t)\)构成，表达式的常数项不会受到\(t\)变化的影响，\(r(t)\)的常数项称为稳态响应。\(r(t)\)中受到\(t\)影响的部分称为瞬态响应。

系统稳定性

s域图像

由\(s=σ+jω\),因此可以将任何一个值在以实部\(σ\)为横轴，虚部\(jω\)为纵轴的s域中的一个点来表示。
在s域图像中，系统方程的极点以×表示，系统方程的零点以◯表示。

连续系统的稳定性

在时域中有： \[∫|h(t)|dt<∞\] 满足上述条件的系统是稳定系统。
在s域中，如果所有的极点都在s域图像的左侧，即\(σ<0\)，满足系统稳定的条件。当所有极点都在虚轴上且为一阶时，这个系统是严格的稳定系统。

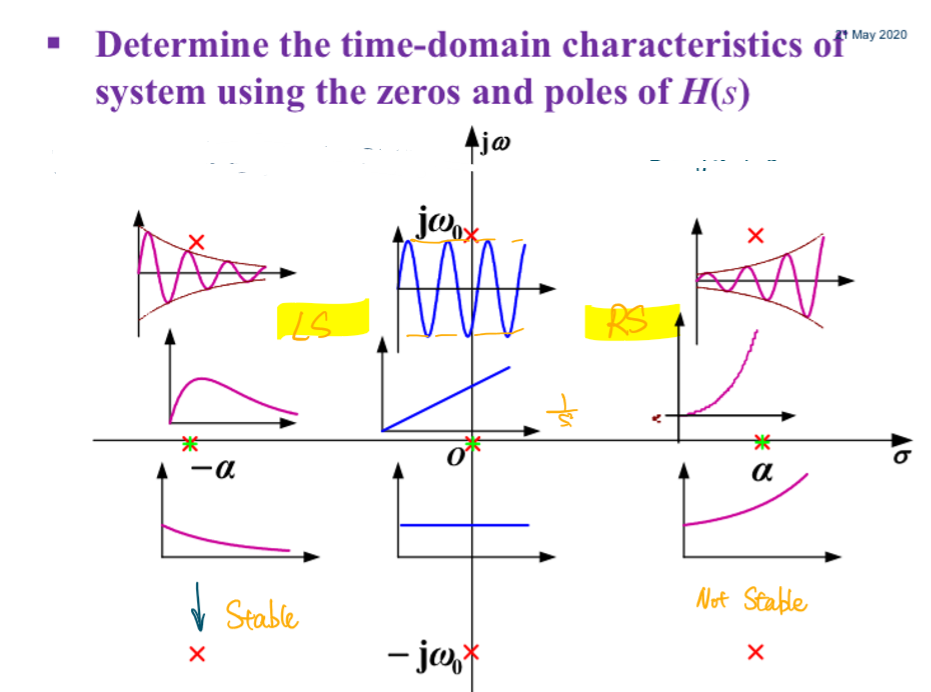
离散系统的稳定性

由\(z=e^{sT}\)，当\(s=0\)时，\(z=1\)，因此如果极点在z域的单位圆内，离散系统是稳定系统，在单位圆外，系统是非稳定系统。

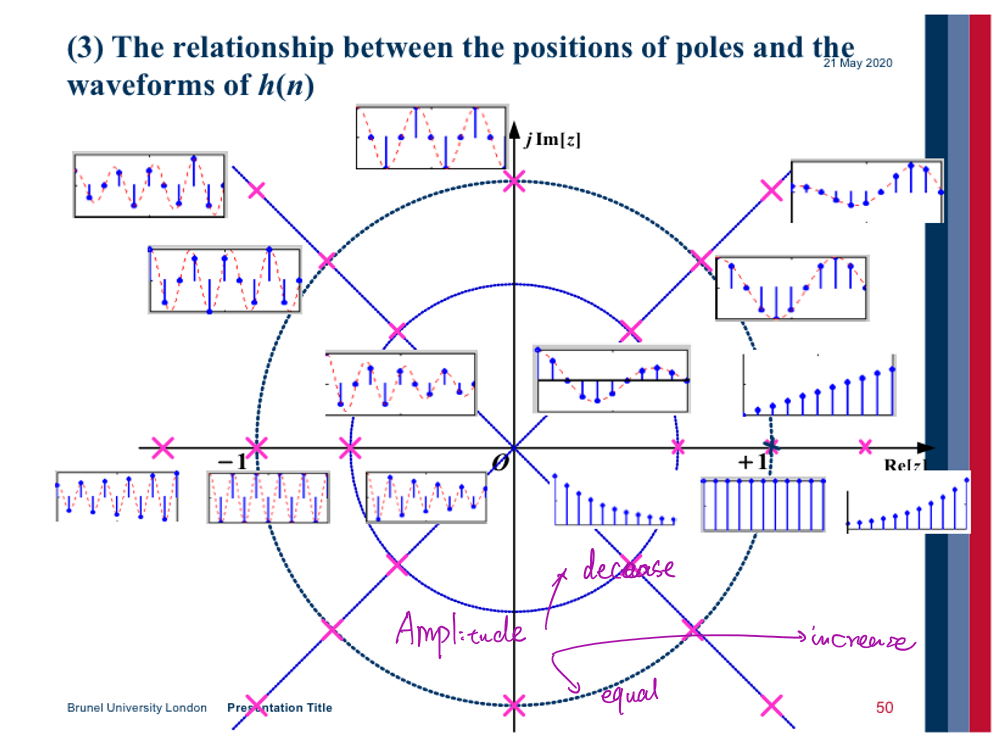
由连续系统稳定性推导离散系统稳定性的过程：控制系统：数字系统稳定性