11. 滤波器设计

滤波器设计

失真

系统方程\(H(s)\)可以写作： \[H(jω)=|H(jω)|e^{jϕ(jω)}\] 即幅值和相位两部分。系统输出的实质是对系统方程的频率和赋值用\(E(jω)\)进行加权。
如果不同频率信号的幅值加权或相位校正不同，则输出波形将与输入波形形状不同，从而导致失真。 失真分为两种类型：
线性失真：信号的幅值和相位发生变化，但是没有引入新的频率信号。
非线性失真：引入了新的频率信号。

滤波器波形

实际的滤波器波形如图表示：

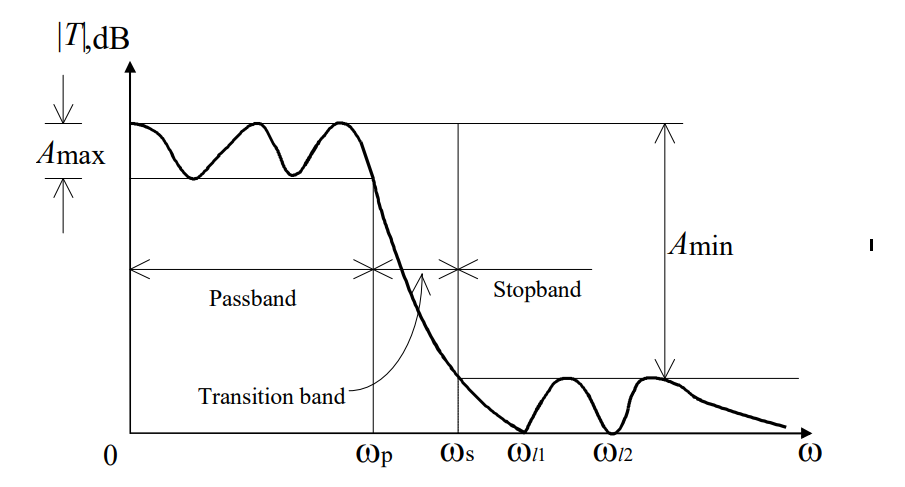
滤波器波形的四个参数： 1. 通带边缘（Passband edge,\(ω_p\)） 2. 最大允许变化（Maximum allowed variation,\(A_max\)） 3. 阻带边缘（Stopband edge,\(ω_s\)） 4. 最小阻带衰减要求（Minimum required stopband attenuation,\(A_min\)）

滤波器设计

(低通)滤波器类型

巴特沃斯滤波器

传递函数： \[|T(jω)|=\frac{1}{√(1+ϵ^2(\frac{ω}{ω_p})^(2n))}\] 其中：\(n≥\frac{logM}{logΩ}\)为电路阶数，\(ϵ=√{10^{\frac{A_{max}}{10}}-1}\)
\(Ω=\frac{ω_s}{ω_p}\)，\(M=√{\frac{\frac{1}{K_A}-1}{\frac{1}{K_r-1}}}\)

滤波器特点：
1. 没有波纹 2. \(|ω_s-ω_p|\)较大，无法立刻停止

切比雪夫滤波器

传递函数： \[|T(jω)|=\frac{1}{√1+ϵ^2C^2_n(ω/ω_p)}\] 其中：\(n≥\frac{cosh^{-1}M}{cosh^{-1}Ω}\)为电路阶数，\(ϵ=√{10^{\frac{A_{max}}{10}}-1}\)
\(Ω=\frac{ω_s}{ω_p}\)，\(M=√{\frac{\frac{1}{K_A}-1}{\frac{1}{K_r-1}}}\)

将电感和电容对换就可以得到高通滤波器。

设计方法

1. 确定使用的滤波器类型
   
2. 找到能够拟合要求的传递函数（巴特沃斯/切比雪夫）
   
3. 根据波形图求出电路的最小阶数\(n\)
   
4. 查表找到CL的数值，并作反归一化
   
5. 连接电路