常考知识点总结
本文最后更新于 2025年9月1日 上午
常考知识点总结
针对Brunel University 2021: EE2622 Fundamentals of Signals and Systems 的期末复习笔记
Lecturer: Dr. Ruiheng Wu (武瑞恒)
信号的基本分类*
连续信号:x轴,y轴都连续 离散信号:x轴连续的信号 数字信号:x轴,y轴都连续的信号
- 三角离散信号的采样周期和周期
对于离散信号\(sin(ω_0n)\),如果其连续信号角频率为\(Ω\),其取样为\(sin(ω_0n)=sin(ΩTn)\),其周期: \[\frac{2π}{ω_0}=\frac{N_{dis}}{T_{con}}\]
其中\(N_{dis}\)为离散信号的周期,\(T_{con}\)为连续信号的周期。
> 如果两者的比值不是一个有理数,那么其离散信号不是一个周期函数。
冲激函数的特性
冲激函数的特性
| 特性 | 公式 |
|---|---|
| 赋值性 | \(∫δ(t)f(t)dt=f(0)\) |
| \(f(t)δ(t)=f(0)δ(t)\) | |
| 偶函数 | \(δ(t)=δ(-t)\) |
| 缩放 | \(δ(at)=\frac{1}{ ⃒ a ⃒ }δ(t)\) |
冲激函数的应用
单位冲激函数可以描述带有间断点函数的倒数。
单位冲激函数可以描述门函数的导数。
冲激偶函数的特性
| 特性 | 公式 |
|---|---|
| 赋值性 | \(∫δ'(t)f(t)dt=-f'(0)\) |
| \(f(t)δ'(t)=f(0)δ'(t)-f'(0)δ(t)\) | |
| 奇函数 | \(δ'(t)=-δ'(t)\) |
信号的表示
- 有限重复非周期的信号: 利用时移进行表示
- “/-”信号(斜坡和阶跃信号的组合)是门信号的积分结果。
信号的微分关系
\[tu(t)→u(t)→δ(t)→δ'(t)\]
\(δ(t)\)有关的性质都用积分相等进行证明。
\[/-信号→G(t)→δ(t)的组合\] 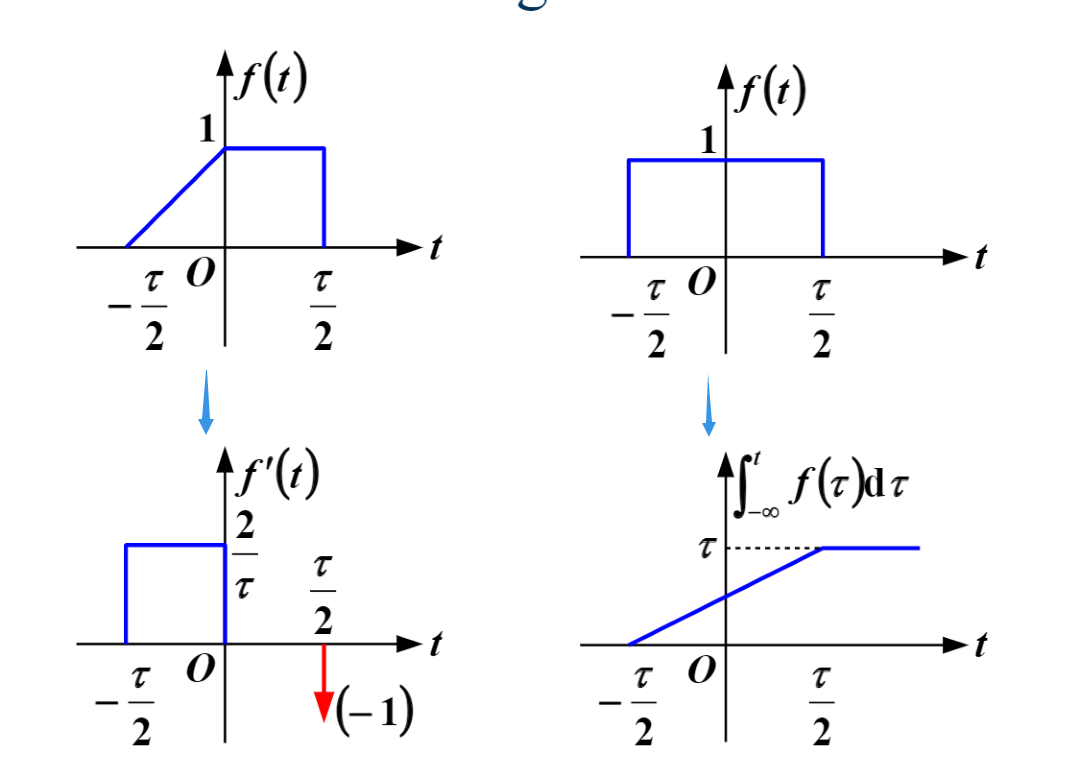
信号的基本操作
时移和尺度变换
对\(f(at+b)\),其化为\(f(a(t+\frac{b}{a}))\)后对\(f(t)\)的图像先缩放\(\frac{1}{a}\),再向左平移\(\frac{b}{a}\)个单位。
信号的分解*
奇偶分解:\(f(t)=\frac{1}{2}[f(t)+f(-t)]_{even}+\frac{1}{2}[f(t)-f(-t)]_{odd}\)
复数分解:\(f(t)=\frac{1}{2}[f(t)+f^\*(t)]_{real}+\frac{1}{2}[f(t)-f^\*(t)]_{img}\)
直流分解: \(f(t)=[\frac{1}{T}∫_{t_0}^{T+t_0}f(t)dt]_{dc}+f_A(t)\)
信号的能量(帕塞瓦尔定理)
信号\(f(t)\)的总能量可以用如下公式表示:
\[P=∫|f(t)|^2dt=\frac{1}{2π}|F(jω)|^2dω\]
注意:|F(jω)|指模长
信号的频谱
周期信号的频谱是离散频谱,非周期信号的频谱是连续频谱。 通过傅里叶级数写出信号频谱的办法:
- 将傅里叶级数转化为cos的形式: \(f(t)=∑A_ncos(nω+ϕ_n)\)
- 对于单边频谱,根据nω直接写出\(A_n\)或者\(ϕ_n\)的频谱
双边频谱的幅值谱是\(\frac{A_n}{2}\)。
门信号的傅里叶系数/频谱
门信号的傅里叶系数\(F(nω)=\frac{1}{2}a_n\)
其频谱最重要的三个参数:
幅值:\(F(nω)max\) 谐波宽度:\(ω_0=\frac{2π}{T}\),只与\(T\)有关。
主瓣宽度,\(F(nω)=0\),\(\frac{2π}{τ}\),只与\(τ\)有关。
系统的性质
因果性
\(t_0\)时刻,系统输出只与\(f(t_0)\)和\(f(t<t_0)\)有关。
也就是说输出的\(f(t)\)和输入的\(t_0\)相比,\(t_0>t\)。(例如\(x(-t)\) 输入\(t=-4\)时,输出为\(x(4)\),\(4>-4\)因此不是因果系统)
线性
满足: \[H[C_1f_1(t)+C_2f_2(t)]=C_1H[f_1(t)]+C_2H[f_2(t)]\]
稳定性
满足: \[ \lim_{t→∞}f(t)<∞\]
通常判断系统稳定性从系统方程入手,判断s域下极点是否在左半轴或者z域中极点是否在单位圆内。
时不变性*
先变换,后时移与先时移,后变换的结果相同。
傅里叶变换
周期信号的傅里叶级数
\[f(t)=a_0+∑_{n=1}^∞[a_n cos(nω_1t)+b_nsin(nω_1t)]\] 组成成分:
直流分量:\(a_0=\frac{1}{T}∫_0^Tf(t)dt\),表示一周期内信号的平均值。
基波分量:\(a_n=\frac{2}{T}∫_0^Tf(t)cos(nω_1t)dt\)
谐波分量:\(b_n=\frac{2}{T}∫_0^Tf(t)sin(nω_1t)dt\)
注意当\(f(t)\)是一个奇函数时,\(a=0\);\(f(t)\)是一个偶函数时,\(b=0\)。
指数形式的傅里叶级数:
\[f(t)=∑F(nω_1)e^{jnω_1t}\] \(F(nω_1)=\frac{1}{2}(a_n-jb_n)\)
幅度:\(|F(nω_1)|=\frac{1}{2}√{a_n^2+b_n^2}\)
相位:\(φ_n=arctan(-\frac{b_n}{a_n})\)
非周期函数的傅里叶变换
\[F(ω)=∫f(t)e^{-jωt}dt=F[f(t)]\] 复数形式:\(F(ω)=|F(ω)|e^{jφ(ω)}\)
傅里叶反变换:
\[f(t)=\frac{1}{2π}∫F(ω)e^{jωt}dω\]
周期信号的傅里叶变换
如果周期函数\(f_T(t)\)一个周期内的子函数为\(f(t)\),那么\(f_T(t)\)的傅里叶变换可以写作:
\[F_T(ω)=2π∑F(nω_1)δ(ω-nω_1)\] 其中\(F(nω_1)=\frac{1}{T}F(ω)|_{ω=nω_1}\) 因此上式可以化简为:
\[F_T(ω)=ω_1∑F(ω)|_{ω=nω_1}δ(ω-nω_1)\]
傅里叶变换的运算性质
| 注解 | 时域 | 频域 |
|---|---|---|
| 对偶性 | \(2πf(-ω)\) | \(F(t)\) |
| 尺度变换 | \(f(at)\) | \(\frac{1}{\lvert a\rvert}F(\frac{ω}{a})\) |
| 时移 | \(f(t-t_0)\) | \(F(ω)e^{-jωt_0}\) |
| 频移 | \(f(t)e^{-jω_0t}\) | \(F(ω+ω_0)\) |
| 时域微分 | \(f'(t)\) | \(jωF(ω)\) |
| 频域微分 | \(-jtf(t)\) | \(F'(ω)\) |
| 时域积分 | \(∫f(t)dt\) | \(πF(0)δ(ω)+\frac{F(ω)}{jω}\) |
常见信号的傅里叶变换
| 名称 | 时域函数\(f(t)\) | 频域函数\(F(ω)\) |
|---|---|---|
| 门函数 | \(E[u(t+\frac{τ}{2})-u(t-\frac{τ}{2})]\) \(E,-\frac{τ}{2}<t<\frac{τ}{2}\) |
\(\frac{2Esin(ω\frac{τ}{2})}{ω}=EτSa(\frac{ωτ}{2})\) |
| 直流信号/常函数 | \(E\) | \(2πEδ(ω)\) |
| 冲激函数 | \(δ(t)\) | \(1\) |
| 冲激偶函数 | \(δ'(t)\) | \(jω\) |
| 阶跃函数 | \(u(t)\) | \(\frac{1}{jw}+πδ(ω)\) |
| 单侧指数函数 | \(Ee^{-at}u(t)\) | \(\frac{E}{jω+a}\) |
| - | - | - |
| 周期冲激序列 | \(δ_T(t)\) | \(ω_1δ(ω-nω_1)\) |
| 周期方波/门函数序列 | - | \(EτSa(\frac{ωτ}{2})ω_1δ(ω-nω_1)\) |
| 正弦函数 | \(sin(ω_0t)\) | \(-jπδ(ω-ω_0)+jπδ(ω+ω_0)\) |
| 余弦函数 | \(cos(ω_0t)\) | \(πδ(ω-ω_0)+πδ(ω+ω_0)\) |
采样定理
奈奎斯特采样率:\(f_n=2f_m\), 采样频率\(f_n\)是输入信号的频率的两倍。
时域分析方法
卷积
定义: \[∫f(t)h(τ-t)dt=f(t)*h(t)\] 称为信号的卷积运算。
运算性质:
- \(f(t)*δ(t)=f(t)\)
- \(f(t)*δ(t-t_0)=f(t-t_0)\)
- \(f(t)*δ'(t)=f'(t)\)
- 图解法解卷积运算 对于简单的信号,可以采取翻转其中一个信号,将这个信号图像平移,平移过程中观察与另一个信号图像的重叠面积的变化。
冲激响应和阶跃响应
当输入信号为\(δ(t)\)时,系统的输出为\(h(t)\),称为单位冲激响应。
当输入信号为\(u(t)\)时,系统的输出为\(g(t)\),称为单位阶跃响应。
冲激响应和阶跃响应满足如下关系:
\[g(t)=∫_{-∞}^th(t)dt\]
由于卷积运算中\(f(t)h(τ-t)≠0\),因此阶跃响应可以用于决定积分的上下限。
零状态和零响应
零输入响应:没有任何输入时系统的响应,对应系统的特征微分方程输入为0的情况。
初始状态的值会直接影响到零状态响应:如果初始状态\(x(0)=c\)对应的零输入响应为\(r_{zs}^i\),那么初始状态为\(x(0)=2c\)对应的零输入响应为\(r_{zs}^{ii}=2r_{zs}^i\)
零状态响应:不考虑系统的初始状态,系统输入对系统造成的响应。
系统的零状态响应可以表示为输入信号为\(δ(t)\)时的系统响应与系统输入信号的卷积:
\[r_{zs}=h(t)*e(t) ↔ R_{zs}(s)=H(s)E(s)\] 系统的全响应: 系统的零状态响应和系统的零输入响应之和。
\[R(s)=H(s)E(s)+R_{zi}(s)\]
时域分析法解系统微分方程
求齐次解(零输入响应)
系统的齐次解方程:
\[f[y(t)]=0\]
将特征方程转化为多项式并求解。
对于微分方程的特征方程,其\(n\)阶微分项可以被换元为\(α^n\)项,最终将特征方程转化为关于\(α\)的\(n\)阶多项式。
对于差分方程的特征方程,其0阶差分项\(y(n)\)可以被换元为关于\(α\)的最高幂项,如此类推,最终将特征方程转化为关于\(α\)的\(n\)阶多项式。
根据多项式的解的个数和是否有重根,可以在下表中找到齐次解的形式,并带入多项式的解。
不同特征根所对应的齐次解(微分方程)
特征根 齐次解\(y_p(t)\) 单实根 \(e^{αk}\) r重实根 \(∑C_{r-1}t^{r-1} e^{αk}\) 不同特征根所对应的齐次解(差分方程)
特征根 齐次解\(y_p(k)\) 单实根 \(Cα^k\) r重实根 \(∑C_{r-1}k^{r-1} α^k\)
求系统特解(单位冲激响应)
- 带入具体的激励\(e(t)=δ(t)\)到系统的微分/差分方程。
- 通过0阶项\(r(t)\)与激励中最高次数项之间系数的关系,用待定系数法猜想系统响应\(r(t)\)的结构。
- 将\(r(t)\)的结构代回微分/差分方程,利用对应阶数项系数相等建立方程,解出\(r(t)\)结构中的常系数。
如果已知了一些特解,求另一些特解,可以使用迭代法。
即从\(h(0)\)开始列出微分方程,直到列到所求的特解对应的微分方程,将已知的特解带入,从而求出未知的特解。
拉普拉斯变换
傅里叶变换的局限性
- 对不满足狄利克雷条件的函数无法变换
- 难以求解无穷积分
拉普拉斯变换对
拉普拉斯变换:\(F(s)=L[f(t)]=∫f(t)e^{-st}dt\)
拉普拉斯反变换:\(f(t)=\frac{1}{2πj}∫F(s)e^{st}ds\)
拉普拉斯变换通过向傅里叶变换中添加衰减系数\(e^{-σ}\)来改善\(f(t)\)的收敛性,使其更可能满足狄利克雷条件。
实际上对于反变换,更多的是利用多项式除法,观察多项式的结构来进行反变换: \(F(s)=∑\frac{k}{s-p}↔f(t)=∑ke^{pt}\) (一阶实极点)
如果分子是含有s的表达式,尝试用\(A-\frac{C}{f(s)}\)的形式进行表达,常数部分转化为冲激函数。
拉普拉斯变换的运算性质
| 注解 | 时域 | 频域 |
|---|---|---|
| 时移 | \(f(t-t_0)\) | \(F(ω)e^{-t_0s}\) |
| 频移 | \(f(t)e^{-at}\) | \(F(s+a)\) |
| 尺度变换 | \(f(at)\) | \(\frac{1}{\lvert a\rvert}F(\frac{s}{a})\) |
| 时域微分(一阶) | \(f'(t)\) | \(sF(s)-f(0)\) |
| 时域微分(二阶) | \(\frac{df^2(t)}{dt}\) | \(s[sF(s)-f(0)]-f'(0)\) |
| 频域微分 | \(t^nf(t)\) | \((-1)^n\frac{d^nF(s)}{ds^n}\) |
| 时域积分 | \(∫f(t)dt\) | \(\frac{F(s)}{s}+\frac{f'(0)}{s}\) |
| 频域积分 | \(\frac{f(t)}{t}\) | \(∫F(s)ds\) |
初值定理: \(f(0_+)\lim_{s→∞}sF(s)\)
终值定理:\(\lim_{t→∞}f(t)=\lim_{s→0}sF(s)\)
卷积理论:\(L[f(t)h(t)]=\frac{1}{2πj}F(s)*H(s)\)
常见信号的拉普拉斯变换
| 名称 | 时域函数\(f(t)\) | 频域函数\(L(s)\) |
|---|---|---|
| 阶跃函数 | \(u(t)\) | \(\frac{1}{s}\) |
| 冲激函数 | \(δ(t)\) | \(1\) |
| 单侧指数函数 | \(Ee^{-at}u(t)\) | \(\frac{E}{s+a}\) |
| 斜坡函数 | \(tu(t)\) | \(\frac{1}{s^2}\) |
| 正弦函数 | \(sin(ω_0t)\) | \(\frac{ω_0}{s^2+ω_0^2 }\) |
| 余弦函数 | \(cos(ω_0t)\) | \(\frac{s}{s^2+ω_0^2}\) |
利用拉普拉斯变换求微分方程
以时域函数\(f(t)\)的拉普拉斯变换\(F(s)\)的微分特性:
一阶微分:\(\frac{df(t)}{dt}→sF(s)-f(0\_ )\)
二阶微分:\(\frac{df^2(t)}{dt}→s[sF(s)-f(0\_ )]-f'(0\_ )\)可以将微分方程以拉普拉斯变换从时域变换至频域。
对于描述系统的微分方程将其做拉普拉斯变换: \[F_{out}(R(s),s)=F_{in}(E(s),s)\]带入初始条件和给定的题目条件中的一些\(r(t)\)在特定时刻下的值,得到方程
解出频域内的\(R(s)\)
用待定系数法展开多项式分式并用拉普拉斯反变换得到\(r(t)\)
注意初始条件
对于全响应方程\(R(s)\),\(R(s)\)可以分解为两部分,一部分只与初始状态\(r(0)\)相关(零输入响应),另一部分方程只与输入\(E(s)\)有关(零状态响应)。对这两部分分别进行拉普拉斯反变换得到零输入响应和零状态响应。
Z变换
Z变换对
Z变换:\(X(z)=∑x(n)z^{-n}\)
收敛域:\(∑|x(n)z^{-n}<∞|\)
Z反变换:\(X(z)=z(\frac{A}{z-p_i})⟷x(n)=∑A(p_i)^n\)(一阶单极点)
收敛域*
\[∑∣x(n)z^{-n}∣<∞\]
Z变换的运算性质
| 注解 | 时域 | 频域 |
|---|---|---|
| 双侧时移 | \(x(n+m)\) | \(z^mX(z)\) |
| 右侧时移 | \(x(n-m)\) | \(z^{-m}[X(z)+∑_{k=-m}^{-1}x(k)z^{-k}]\) |
| 尺度变换(时域) | \(nx(n)\) | \(-z\frac{dX(z)}{dz}\) |
| 尺度变换(z域) | \(a^nx(n)\) | \(X(\frac{z}{a})\) |
初值定理: \(x(0_+)\lim_{x→∞}X(z)\)
终值定理:\(\lim_{n→∞}x(n)=\lim_{z→1}(z-1)X(z)\)
卷积理论:\(Z[x(n)*h(n)]=X(z)H(z)\)
常见信号的Z变换
| 名称 | 时域序列\(x(n)\) | 频域序列\(X(z)\) | 收敛域 |
|---|---|---|---|
| 单位冲激序列 | \(δ(n)\) | \(1\) | 整个z域 |
| 单位阶跃序列 | \(u(n)\) | \(\frac{z}{z-1}\) | \(⃒ z ⃒ <1\) |
| 斜坡序列 | \(nu(n)\) | \(\frac{z}{(z-1)^2}\) | \(⃒ z ⃒ <1\) |
| 单侧指数序列 | \(a^nu(n)\) | \(\frac{z}{z-a}\) | \(⃒ z ⃒ >⃒ a ⃒\) |
| 单侧正弦序列 | \(sin(ω_0n)u(n)\) | \(\frac{zsinω_0}{z^2-2zcosω_0+1}\) | \(⃒ z ⃒ >1\) |
| 单侧余弦序列 | \(cos(ω_0n)u(n)\) | \(\frac{z(z-cosω_0)}{z^2-2zcosω_0+1}\) | \(⃒ z ⃒ >1\) |
利用Z变换求差分方程
利用Z变换的单边右时移特性:
\(x(n-1)=z^{-1}X(z)+x(-1)\)
\(x(n-2)=z^{-2}X(z)+z^{-1}x(-1)+x(-2)\)
注意初始条件
- 将差分方程改写成Z变换的形式
- 确定初始状态,解出差分方程
- 反变换得到\(y(n)\)
系统方程
描述系统的方程\(H(s)=\frac{R(s)}{E(s)}\)
\(H(s)\)的分母为系统微分方程输入侧的特征方程,分子为系统输出侧的特征方程。
系统输入和输出在s域内都以多项式表示,系统方程自然是两个多项式的比值: \[H(s)=\frac{R(s)}{E(s)}=K\frac{Π(s-z_i)}{Π(s-p_k)}\] 其中\(p_i\)称为系统方程的极点,\(z_k\)称为系统方程的零点。
系统稳定性
在s域图像中,如果极点分布在s域的左半轴,表明系统是稳定的。
在z域图像中,如果极点分布在z域的单位圆内,表明系统是稳定的。
反馈系统的方程
如图:

系统的闭环传递函数:
\[\frac{C(s)}{R(s)}=\frac{G(s)}{1+G(s)H(s)}\] 其中:系统的开环传递函数为\(G(s)H(s)\)。
根轨迹图
系统的开环传递函数加入了一个根轨迹增益\(K\)以衡量闭环极点对开环传递函数的影响。
得到根轨迹图的步骤:
- 通过闭环传递函数的特征方程\(1+G(s)H(s)=0\)解出s与参数\(K\)之间的关系。
注意开环传递函数的特征方程是\(1+G(s)H(s)=0\)
二阶多项式方程的根:\(\frac{-b⨦√Δ}{2a}\)
- 在s域中标出零点。
- 在s域中标出极点,即\(K=0\)的位置。
- 增加K的值,在S域中标出一系列的s的位置,并以(\(K=x\))在每个点上方进行标注。
- 判断\(k→∞\)时,s的移动方向,并用箭头标注。
切比雪夫滤波器
特点
- 过渡带很小
- 有波纹
参数
实际的滤波器波形如图表示:
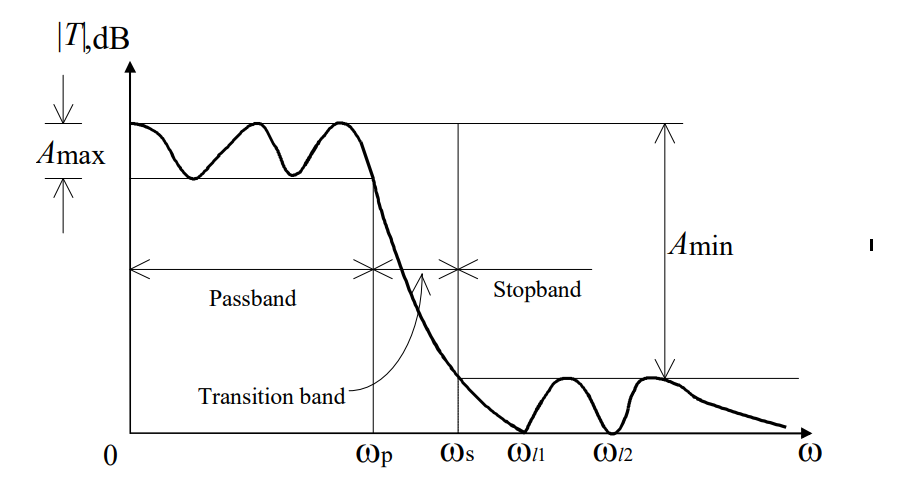
滤波器波形的四个参数:
- 通带边缘(Passband edge,\(ω_p\))
- 最大允许变化(Maximum allowed variation,\(A_{max}\))
- 阻带边缘(Stopband edge,\(ω_s\))
- 最小阻带衰减要求(Minimum required stopband attenuation,\(A_{min}\))
传递函数(低通)
\[|T(jω)|=\frac{1}{√1+ɛ^2C^2_n(ω/ω_p)}\] 其中:\(n≥\frac{cosh^{-1}M}{cosh^{-1}Ω}\)为电路阶数,\(ɛ=√{10^{\frac{A_{max}}{10}}-1}\)
\(Ω=\frac{ω_s}{ω_p}\)(称为选择因子(Select Factor)),\(M=√{\frac{\frac{1}{K_A}-1}{\frac{1}{K_r-1}}}\)
切比雪夫高通滤波器
将电感和电容对换就可以得到高通滤波器。
和原来的低通滤波器相比,新的高通滤波器\(ω_p\)相同,\(ω_s'=\frac{ω_p^2}{ω_s}\)。
设计方法
- 确定使用的滤波器类型
- 找到能够拟合要求的转换方程(巴特沃斯/切比雪夫)
- 根据波形图求出电路的最小阶数\(n\)
- 查表找到CL的数值,并作反归一化
- 连接电路