01. 运算放大器

运算放大器

结构和特性

一个运算放大器的结构如图所示：

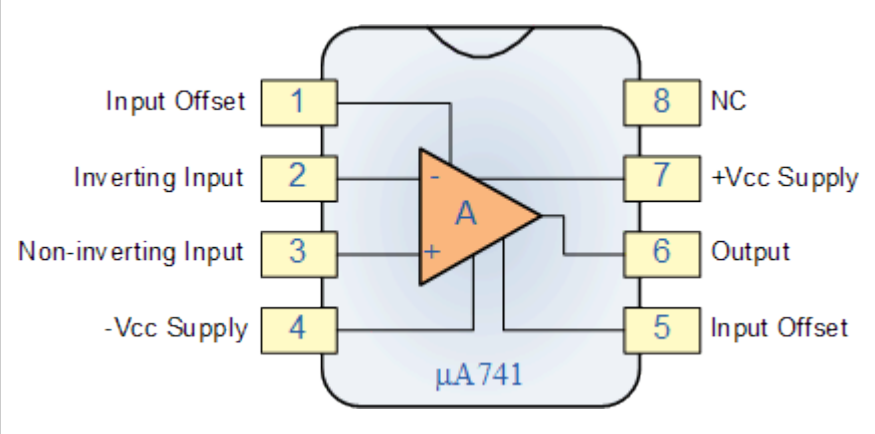
结构

输入和输出

2.反相输入端\(V_{(-)}\)
3.正相输入端\(V_{(+)}\)
6.输出\(V_{out}\)
运算放大器的输入电压\(V_{(in)}\)可以表示为：
\[V_{(in)}=V_{(+)}-V_{(-)}\]

供电

4.7.为两个供电接口，一般来说运算放大器的供电电压在⨦5v~⨦15v之间。

特性

增益

一般来说，运算放大器内部输入端的阻抗非常的大；而内部输出端的阻抗非常的小；同时运算放大器的增益非常大。
运算放大器的（电压）增益：
\[A=\frac{V_{out}}{V_{in}}\] 由于运算放大器的增益常常到了上万级别，而运算放大器本质上是放大两个输入端之间的差异，因此如果两个输入端之间的电压差值过大可能会导致烧坏电路。一般输入端的\(V_{(-)}\)和\(V_{(+)}\)要求：
\[V_{(+)}≈V_{(-)}\]
在理想状态下，运算放大器输入端的阻抗无限大，输出端的阻抗为0，且增益为无限大。

频率响应特性

对于运算放大器而言，随着频率的升高，运算放大器的电压增益会逐渐减小，如下图所示。

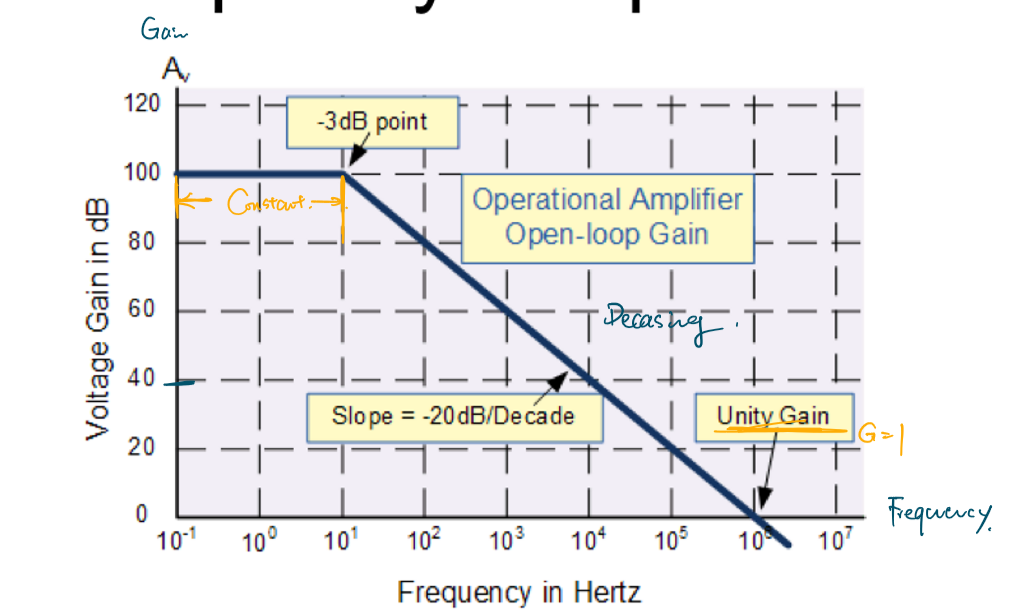
定义在某一频率时的带宽与增益的乘积为增益带宽积（GBP）：
\[GBP=Gain × Bandwidth\]

理想放大器的特性

一般认为理想放大器在反相输入端和同相输入端之间存在两个特性，方便进行电路分析：
1. 理想放大器的反相输入端和同相输入端之间的电压是相等的，称为“虚短路”。
2. 当其中一输入端口端直接接地时，理想放大器的反相输入端和同相输入端之间的电压是为“0”的，称为“虚接地”。

基本电路

反相放大器

反相放大器的电路连接如图所示：

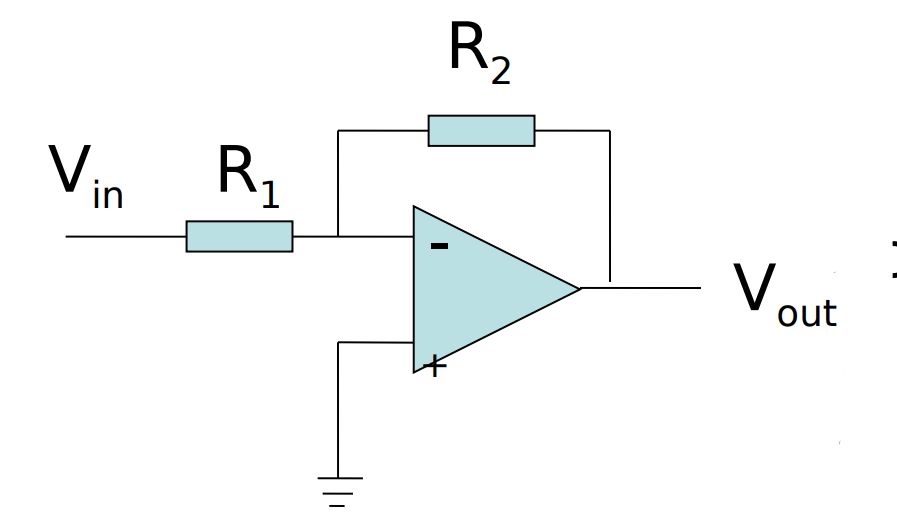
增益

运算放大器的推导建立在两个基本条件之上：
1. 由于\(V_{(+)}≈V_{(-)}\)，因此输入端的+-输入间可以视为通路，即\(V_{(+)}=V_{(-)}\)。
2. 人为地使得电阻\(R_1\)和\(R_2\)的阻值非常大（在千欧姆级别），因此通过-输入端与\(R_1\)之间的电流非常小，这部分电流可以视为0。

反相放大器的增益：
\[A=-\frac{R_2}{R_1}\]
其推导过程简写如下：
\[\begin{aligned} ∵&V_{(+)}≈V_{(-)},V_{(+)}=0 \\ ∴&V_{(+)}=V_{(-)}=0 \\ ∵&I_1=I_2,I_1=\frac{V_{in}-0}{R_1},I_2=\frac{0-V_{out}}{R_2}\\ ∴&\frac{V_{in}-0}{R_1}=-\frac{V_{out}}{R_2}\\ ∴&A=\frac{V_{out}}{V_{in}}=-\frac{R_2}{R_1} \end{aligned}\]

同相放大器

同相放大器的电路连接如图所示：

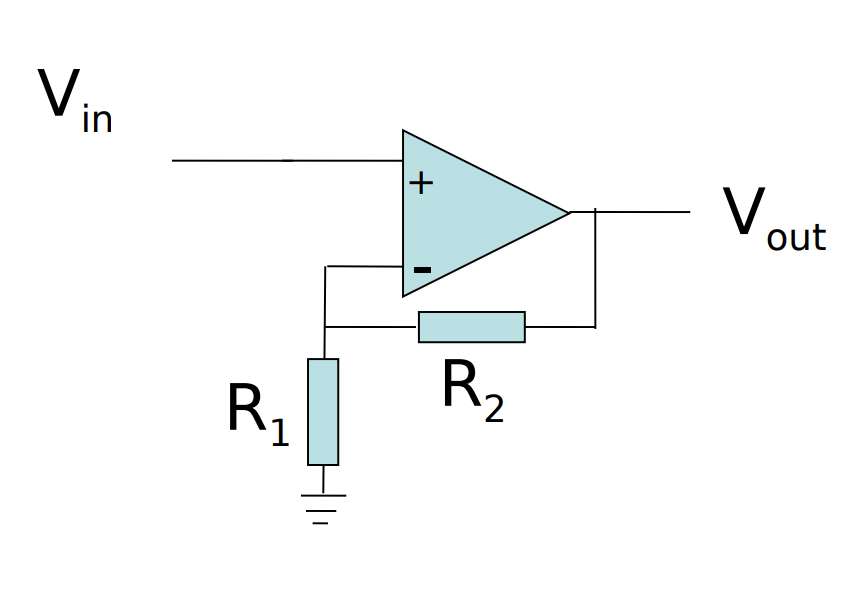
增益

同相放大器的增益：
\[A=1+\frac{R_2}{R_1}\] 其推导过程简写如下：
\[\begin{aligned} ∵&V_{(+)}≈V_{(-)},V_{(+)}=V_{in}\\ ∴&V_{(-)}=V_{(+)}=V_{in}\\ ∵&I_1=I_2,I_1=\frac{V_{in}-0}{R_1},I_2=\frac{V_{out}-V_{in}}{R_2}\\ ∴&\frac{V_{in}}{R_1}=\frac{V_{out}-V_{in}}{R_2}\\ ∴&A=\frac{V_{out}}{V_{in}}=1+\frac{R_2}{R_1} \end{aligned}\]

缓冲器

缓冲器结构如图所示：

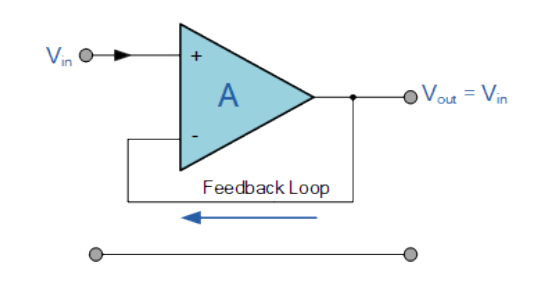
其增益始终为1。
设置缓冲器的目的是为了在不改变电压大小的前提下，对信号的电流进行操作，以补充衰减。 > 信息以电压的形式传输，而电流表征的是携带信息的信号强度

基本电路的应用

加法放大器（反相输入）

加法放大器（Summing Amplifier）的结构如下图所示：

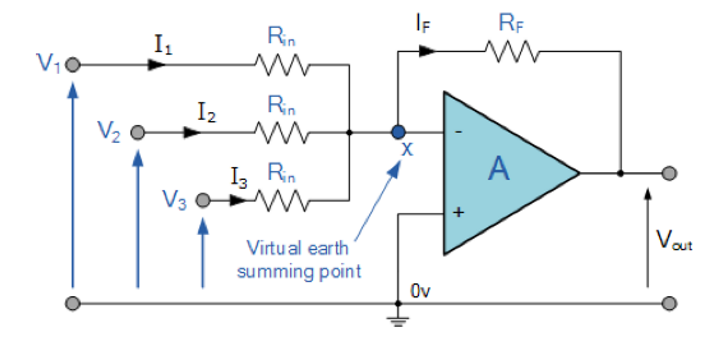
有输入端的各支路电流总和大小等于输出端的电流大小，考虑到虚接地，有：
\[∑\frac{V_{in}}{R_{in}}=-\frac{V_{out}}{R_F}\] 推出：
\[V_{out}=-R_F∑\frac{V_{in}}{R_{in}}\]

加法放大器（反相输入）的增益为：
\[G=\frac{V_{out}}{∑_iV_i}\]

积分器

积分器的电路如下图所示：

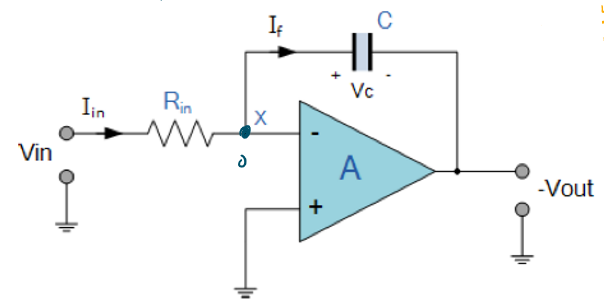
\[V_{out}=-\frac{1}{R_{in}C}∫V_{in}dt\] 其推导过程如下：
\[\begin{aligned} ∵&V_c=\frac{Q}{C}=-V_{out}\\ ∴&\frac{dV_{out}}{dt}=-\frac{dQ}{Cdt}=-\frac{I_F}{C}\\ ∴&I_F=-C\frac{dV_{out}}{dt}\\ ∵&I_{in}=\frac{V_{in}}{R_{in}}\\ ∴&-C\frac{dV_{out}}{dt}=\frac{V_{in}}{R_{in}}\\ ∴&V_{out}=-\frac{1}{R_{in}C}∫V_{in}dt \end{aligned}\]

微分器

微分器的结构如下图所示：

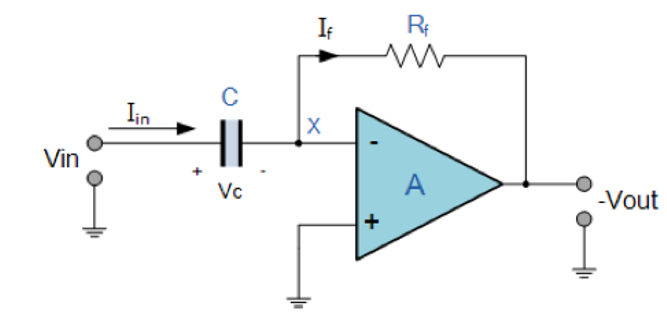
\[V_{out}=-R_FC\frac{dV_{in}}{dt}\] 其推导过程如下：
\[\begin{aligned} ∵&V_c=\frac{Q}{C}=V_{in}\\ ∴&\frac{dQ}{Cdt}=\frac{I_{in}}{C}=\frac{dV_{in}}{t}\\ ∵&I_F=\frac{V_{out}}{R_F},I_F=-I_{in}\\ ∴&V_{out}=-R_FC\frac{dV_{in}}{dt} \end{aligned}\]

差分放大器

与之前的加法器、积分器、微分器不同，差分器使用到了\(V_+\)和\(V_-\)两个输入端，结构如图所示。

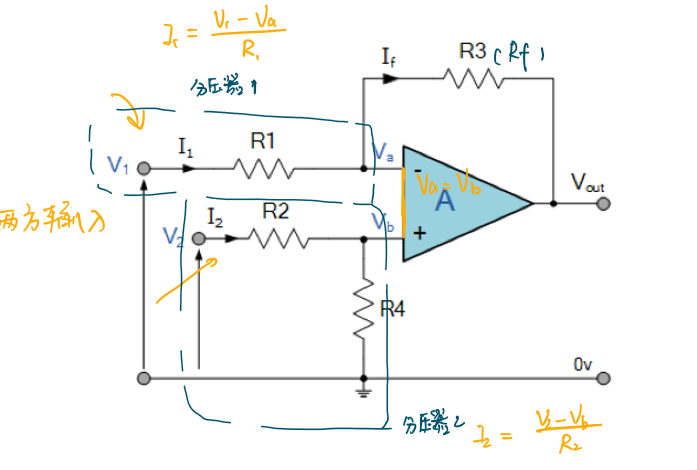
由之前的推理，放大器两个输入端的电压里仍然相等，有\(V_+=V_-\)。同时，根据分压定理：\(V_b=V_2(\frac{R_4}{R_2+R_4})\)。
由叠加定理，单独看两个电压源：
单独看\(V_1\)，有\(V_{out1}=-V_1\frac{R_3}{R_1}\)。
单独看\(V_2\)，有\(V_{out2}=V_2\frac{R_4}{R_2+R_4}\frac{R_1+R_3}{R_1}\)。
所以,
\[V_{out}=-V_1\frac{R_3}{R_1}+V_2\frac{R_4}{R_2+R_4}\frac{R_1+R_3}{R_1}\] 当\(\frac{R_2}{R_1}=\frac{R_4}{R_3}\)时，有： \[V_{out}=\frac{R_3}{R_1}(V_2-V_1)\] 这种设计常常在实际中应用。

差分放大器的增益可以定义为：
\[G=\frac{V_{out}}{V_1-V_2}\]

差分放大器的缺陷

如上图接入的差分放大器有两个缺陷：
1. 由于放大器内部输入端阻抗远远高于外部的两个电阻的阻值，因此实际上电流大部分会通过\(R_4\)流向地面而并非流入运算放大器中。
2. 当\(\frac{R_2}{R_1}=\frac{R_4}{R_3}\)时，差分放大器的增益为: \[Gain=\frac{R_2}{R_1}=\frac{R_4}{R_3}\] 要想改变差分放大器的增益，需要同时改变至少两个电阻以保证条件\(\frac{R_2}{R_1}=\frac{R_4}{R_3}\)依然成立，事实上通过改变至少两个电阻的阻值来改变放大器增益是非常麻烦的。

仪用放大器

为了减小差分放大器的缺陷，在实际运用中做了如下的改进，改进后的差分放大器称为仪用放大器。
对于缺陷1，改进办法是在两个输入端各连接一个缓冲放大器，由于缓冲放大器内部阻抗很高，因此电流不会大量流入接地端。

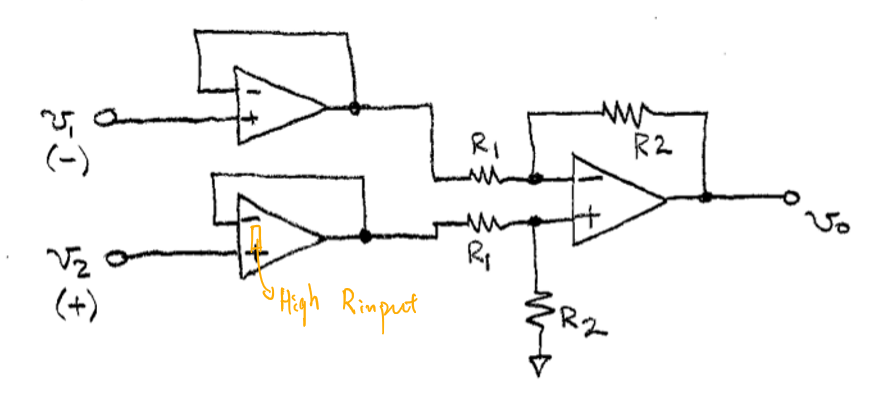
对于缺陷2，改进办法如图所示。下图所示的结构为仪用放大器的结构。

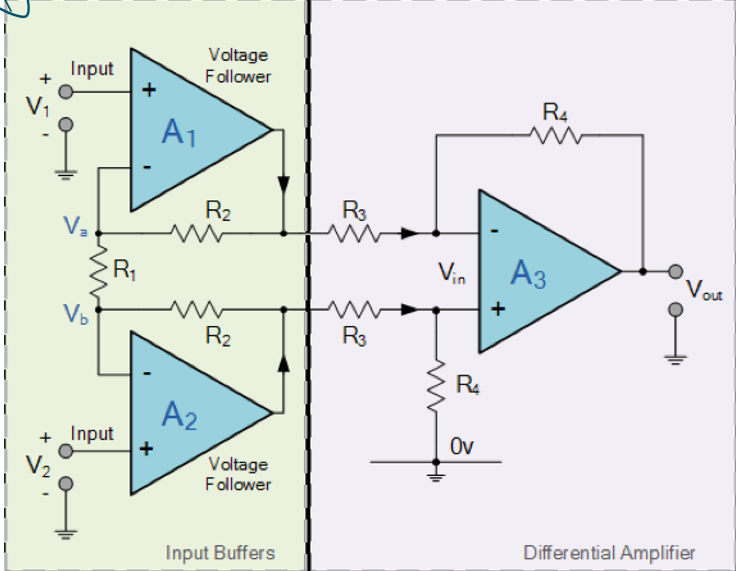
如图所示的电路中\(R_2→R_1→R_2\)（下图蓝色标注）上流过的电流是相等的：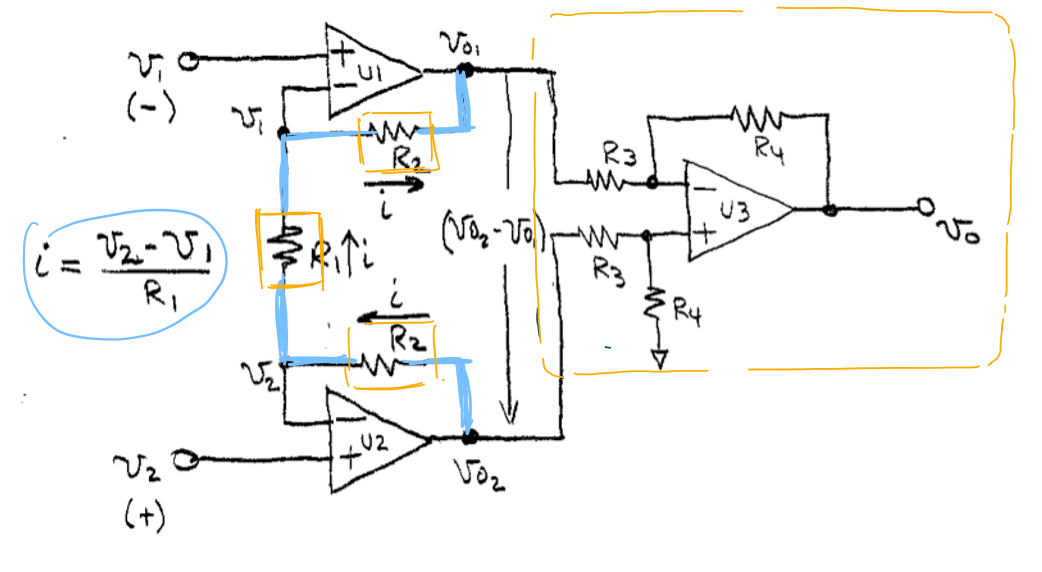

此处的电流为：\(i=\frac{V_2-V_1}{R_1}\)。
此时差分器输入端的电压差可表示为：\(V_{o2}-V_{o1}=i(2R_2+R_1)\)。
带入之前差分放大器的输出电压：\(V_{out}=\frac{R_2}{R_1}(V_2-V_1)\)，得到仪用放大器的输出电压表达式：
\[V_o=\frac{R_4}{R_3}(V_2-V_1)(1+2\frac{R_2}{R_1})\] 仪用放大器的增益：
\[Gain=\frac{R_4}{R_3}(1+2\frac{R_2}{R_1})\] 结合之前的推导可以发现，此时只需要改变\(R_1\)的阻值即可改变增益。
实际上，仪用放大器可以被集成电路化后做成一个8pin的电路元件，其中\(V_k\)和\(V_Y\)两个pin外部连接一个电阻\(R_1\)来改变放大器增益。

共模抑制比

对于差分放大器，之前只讨论了\(\frac{R_2}{R_1}=\frac{R_4}{R_3}\)时的增益。
当\(\frac{R_2}{R_1}≠\frac{R_4}{R_3}\)时，对于\(V_{out}=-V_1\frac{R_3}{R_1}+V_2\frac{R_4}{R_2+R_4}\frac{R_1+R_3}{R_1}\)，很难直接看出差分放大器的增益。所以人为地设置两个新的变量以分离电压，便于求出增益。

设对差模分量：\(V_d=V_2-V_1\)
共模分量：\(V_{cm}=\frac{V_2+V_1}{2}\)
有\(V_1=V_{cm}-\frac{V_d}{2}\)、\(V_2=V_{cm}+\frac{V_d}{2}\)。
带入原来的输出电压表达式中，得到：
\[V_{out}=\frac{1}{2}\frac{R_4}{R_2+R_4}[\frac{R_3+R_1}{R_1}+\frac{R_3}{R_1}]V_d+[\frac{R_3+R_1}{R_1}-\frac{R_3}{R_1}]V_{cm}\] 那么增益可以表示为：
\[Gain=\frac{V_{out}}{V_d}=A_d=\frac{1}{2}\frac{R_4}{R_4+R_2}[\frac{R_1+R_3}{R_1}+\frac{R_3}{R_1}]\] 这个增益称为对差模增益\(A_d\)。
同样地，定义共模增益\(A_{cm}\):
\[A_{cm}=\frac{V_{out}}{V_{cm}}=\frac{R_4}{R_2+R_4}[\frac{R_3+R_1}{R_1}-\frac{R_3}{R_1}]\] 放大器的差模增益是电路所需要的增益，而共模增益将放大直流噪声。共模抑制比（Common Mode Rejection Ratio，CMRR），定义为差模增益与共模增益的比值:
\[CMRR=\frac{A_d}{A_{cm}}\] \[CMRR(dB)=20lg\frac{A_d}{A_{cm}}\]

频率响应特性

放大器的频率响应特性曲线如图所示：

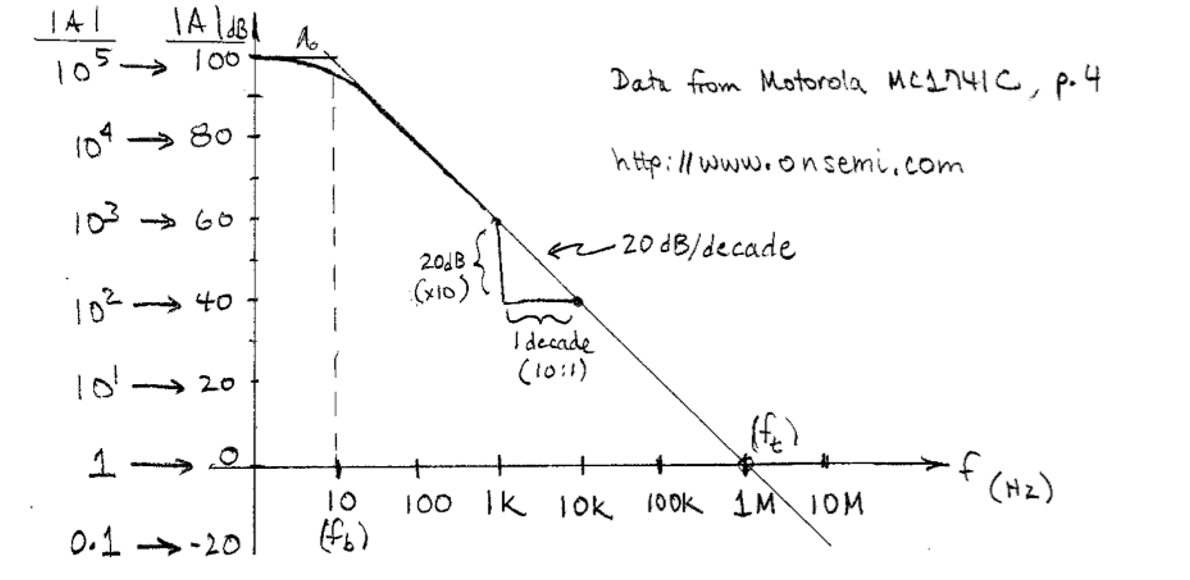
其中：
- \(f_b\)是\(maxgain(dB)-3dB=A_0\)时所对应的频率，一般认为在这个频率后放大器增益不再稳定，随着频率的增大而下降。称\(f_b\)为放大器的截止频率。
- \(f_t\)是增益为0，即1dB时所对应的频率，称为放大器的传输频率。 放大器的频率响应特性表示为：
\[A(f)=\frac{A_0}{1+j(\frac{f}{f_b})}\] 当\(f>>f_b\)时，可以化简为：
\[A(f)=\frac{A_0f_b}{f}\] 当增益为1时，求得传输频率的表达式：
\[f_t=A_0f_b\]

压摆率

理想的运算放大器在输入电压接入运算放大器的同时就会立即有稳定的输出电压，然而实际的运算放大器由于内部电容充电过程的存在，需要经过一小段时间才能达到稳定输出电压\(V_o\)，达到稳定输出电压的最大速率称为压摆率或电压转换速率（Slew Rate）。
\[S.R.=\frac{dV_o}{dt}|_{max}\]
如果输入信号的频率过高，以至于放大器的放大过程跟不上输入信号的变化，放大器的输出信号失真、幅度缩小。
当输出信号是一个正弦波\(y=Asinωt\)时，\(S.R.=Aωcosωt,ωt=0\)。
带入\(ω=2πf\)，得到电压转换速率与放大器输出电压信号的峰值\(A\)、频率\(f\)的关系为:
\[S.R.=2πAf\] 可以得到运算放大器所支持的某峰值下的最大信号频率为：
\[f_{max}=\frac{SR}{2πA}\] \(f_{max}\)称为全功率带宽，这个表达式也暗示可以通过减小信号的峰值使得运算放大器支持更高频率的信号。

泄露和补偿

在真实的放大器中，输入端\(V_+\)和\(V_-\)之间是有电流的，这个电流称为泄露电流，在反相放大器中这个电流会流向\(V_+\)的接地端。泄露电流的存在会造成假设\(V_+=V_-\)不成立，因此在运算放大器的内部需要添加一个补偿电容来对\(V_+\)和\(V_-\)的电压进行补偿。

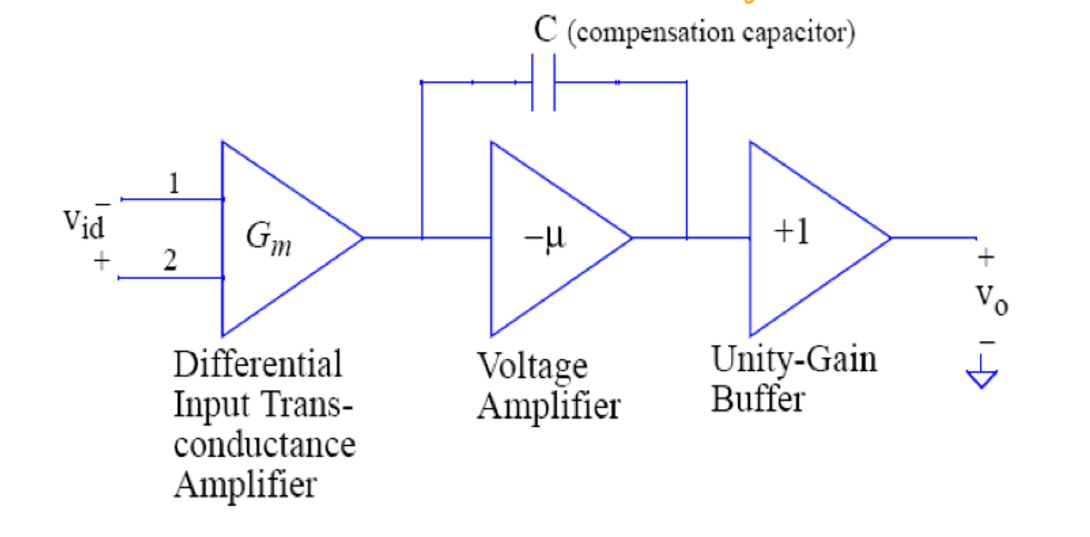
如图所示，当第一级输出的电流\(i_{id}\)为高频率时，电流绕过电压放大器，对电压放大器不会产生影响。
当第一级输出的电流\(i_{id}\)为低频率时，电容断路，电流被消除，但是电压信号仍然可以被放大。

同时在接地端需要额外增加一个补偿电阻以减小泄露电流的影响。在集成化的仪用放大器中，有两个pin：offset用于额外连接一个变阻器，调节补偿电阻的大小。