01. 数字信号
本文最后更新于 2025年6月4日 晚上
数字信号
数字信号是时间离散、幅值离散的信号。但是在本课中为了简化分析,认为时间离散、幅值连续的信号也是数字信号。
数字信号可以由序列进行表示:
\[...,x[-1],x[0],x[1],...\]
采样
模拟信号是时间连续、幅值连续的信号。使模拟信号转变为数字信号的过程称为采样。采样过程可由如下公式表示:
\[x[n]=x(t)|_{t=nT_s}=x(nT_s),n∈Z\] 其中\(T_s\)称为采样周期。
常见的数字信号
单位冲激序列
\[δ[n]=\begin{cases}
1,n=0 \\
0,others
\end{cases}\] 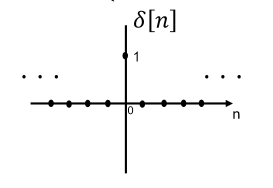
冲激序列的采样性质
类比冲击信号的采样性质,可以发现任何的数字信号都可以表示为时移的单位冲激序列的线性组合。
\[x[n]=∑x[k]δ[n-k]\]
单位阶跃序列
\[u[n]=\begin{cases}
1,n≥0 \\
0,others
\end{cases}\] 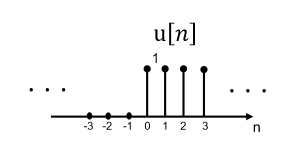
指数序列
\[x[n]=a^n\] 如果底数\(a\)是一个复数:\(a=Ae^{jθ}\),此时可以表示为:
\[x[n]=A^n(cosθn+jsinθn)\] 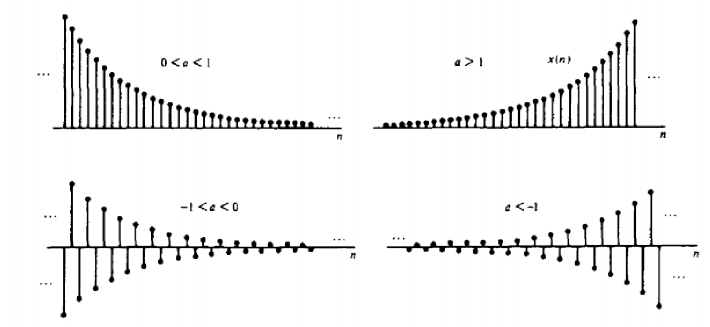
三角序列
连续的三角信号可以表示为:
\[x(t)=Asin(Ωt+φ)\] 此时的角频率\(Ω\)称为模拟角频率,单位为rad/s。
对连续的三角信号进行采样,从而得到数字域的三角信号:
\[x[n]=Asin(2πfn/f_s+φ)=Asin(ωn+φ)\] 其中\(f_s\)是采样频率,\(ω=\frac{2πf}{f_s}\),称为数字角频率,单位为rad或者rad/sample。
数字角频率的理解
由数字角频率:
\[ω=\frac{2πf}{f_s}=\frac{Ω}{f_s}\] 数字角频率可以看做是模拟角频率对其进行归一化的结果。
又有角频率公式:\(ω=2πf_d\),\(f_d\)称为数字频率。
\[f_d=\frac{f}{f_s}\] 数字频率可以看做是对模拟频率\(f\)进行归一化的结果。
三角序列的周期性
定义数字信号的周期性为:
\[x(n)=x(n+N)\] 对于数字三角信号(三角序列),有:
\[Acos(ω_0n+φ)=Acos(ω_0(n+N)+φ)=Acos(ω_0n+ω_0N+φ),0≤ω_0≤2π\] 可以发现当\(ω_0N=2πk,k∈Z\)时上述式子成立。
得到: \[ω_0=\frac{2πk}{N},k=0,1,...,N-1\] 也就是说,要想三角信号呈周期性:
- \(ω_0\)必须是π的整数倍以保证数字周期\(N\)是一个自然数。即存在\(N=\frac{2πk}{ω_0},k=0,1,...,N-1\)则该序列为周期序列。
- 只有N个不同的\(ω_0\)使得三角信号呈周期性。
- 对于复指数序列,使用欧拉公式变换为三角信号,由于cos和sin部分的数字角频率相等,因此可以按照上述判断标准进行判断。
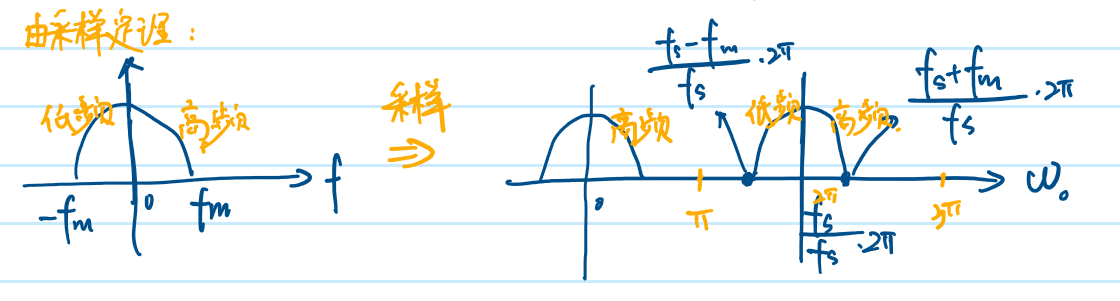
三角序列的振荡特性
对于连续的三角信号:\(Ω\)越大,三角信号的周期越小,三角信号振荡越剧烈。
对于三角序列:
- \(ω∈(0,π)\)时,\(ω\)越大,三角序列振荡越剧烈。
- \(ω∈(π,2π)\)时,\(ω\)越大,三角序列振荡越平缓。
推理的过程如下图所示: