03. 随机变量和随机过程

随机变量和随机过程

由于通信原理所研究的信号是连续的模拟信号，因此本节主要复习连续随机变量/随机过程的性质。

随机变量

概率密度和概率分布函数

对于随机变量\(X\)，概率密度函数(PDF)\(f(x)\)表示当\(X=x\)时候的概率：
\[f(x)=P(X=x)\]

概率分布函数/积累分布函数（CDF）\(F(x)\)表示\(X\)小于\(x\)的概率，对于连续随机变量，积累分布函数可以表示为：
\[F(x)=P(X≤x)=∫_{-∞}^xf(u)du\] 积累分布函数和概率密度函数有如下关系：
\[f(x)=\frac{dF(x)}{dx}\]

概率密度函数的性质

• 正定性：\(f(x)≥0\)
  
• 概率之和为1：\(∫f(x)dx=1\)
• 区间概率：\(P(a<X≤b)=∫_a^bf(x)dx\)

随机变量的统计特征

期望

期望表示随机变量的均值：
\[E(x)=∫xf(x)dx\]

期望的计算性质：
- \(E(C)=C\) - \(E(X+Y)=E(X)+E(Y)\) - 当随机变量\(X\),\(Y\)相互独立时，\(E(XY)=E(X)E(Y)\)

方差

方差表示随机变量分布的离散程度:
\[D(X)=∫[x_i-E(X)]^2f(x)dx\] 更多时候，方差可由期望推导出： \[D(x)=E[X-E(X)]^2=E(X^2)-E^2(X)\] > 求方差的步骤： > 1. 求出期望\(E(X)\) > 2. 求出均方值期望\(E^2(X)\) > 3. 带入公式求得\(D(X)\)

方差的计算性质：
- \(D(C)=0\) - \(D(X+C)=D(X)\) - \(D(CX)=C^2X\) - 当随机变量\(X\),\(Y\)相互独立时，\(D(X+Y)=D(X)+D(Y)\)

通信原理中常见随机变量的分布

均匀分布

均匀分布（Uniform Distribution）指随机变量在某个区间\((a,b)\)内取到某个值\(x\)的概率是相同的。

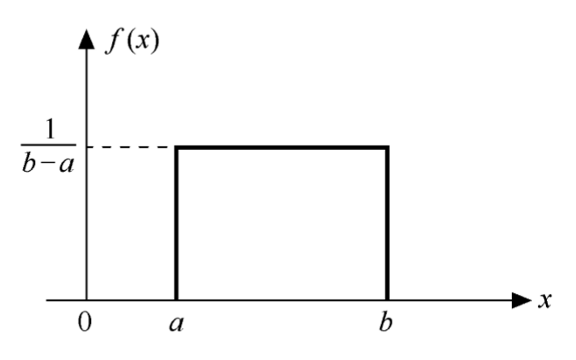
均匀分布的概率密度函数：
\[f(x)=\begin{cases} \frac{1}{b-a},a≤x≤b \\ 0,others \end{cases}\] - 期望：\(E(x)=\frac{b+a}{2}\) - 方差：\(D(x)=\frac{(b-a)^2}{12}\)

高斯分布/正态分布

随机变量在不任何束缚前提下的总体变化规律称为高斯分布/正态分布。

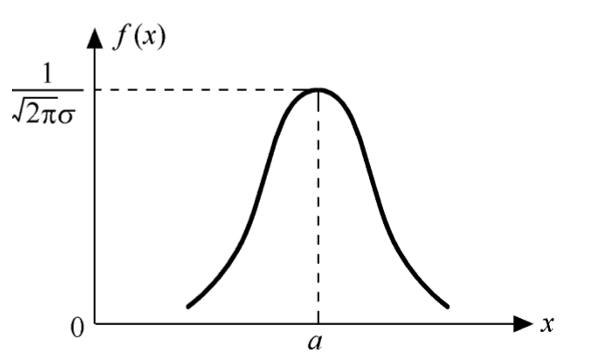
高斯分布的概率密度函数：
\[f(x)=\frac{1}{√(2π)σ}exp[-\frac{(x-μ)^2}{2σ^2}]\] 其中\(μ\)是随机变量\(X\)的均值，它影响高斯分布曲线的轴的位置。
\(σ^2\)是随机变量\(X\)的方差，它影响高斯分布曲线中最大值点的位置。

瑞利分布

当一个随机二维向量的两个分量呈独立的、有着相同的方差、均值为0的 正态分布 时，这个向量的模呈瑞利分布。
瑞利分布的概率密度函数：
\[f(x)=\begin{cases} \frac{x}{σ^2}exp(-\frac{x^2}{2σ^2}),x≥0 \\ 0,x≤0 \end{cases}\] \(σ^2\)是瑞利分布的方差。

随机过程

与上文所述的确知过程不同的是，在每一个时间点上的概率都不能用一个或若干个时间函数进行描述的过程称为随机过程。
随机过程可以有两种理解方式：
1. 在样本空间\(S\)中对每一个样本\(s_i\)采样得到的所有采样函数的集合。
2. 样本空间\(S\)中所有随机变量随着时间的推移。
简单来说，随机过程可以理解为是若干随机变量的集合。
随机过程的阶指随机过程中含有的随机变量的个数。阶数越大，对随机过程的统计特性描述就越充分。

概率密度和概率分布函数

随机过程\(ξ(t)\)在某个固定的时间\(t=t_1\)时是一个随机变量\(ξ(t_1)\)，其一阶概率积累函数可以表示为：
\[F_1(x_1,t_1)=P(ξ(t_1)≤x_1)\] 同样地：
\[f(ξ(t_1))=\frac{∂F_1(x_1,t_1)}{∂x_1}\]

描述随机过程的统计特征

期望

\[E(ξ(t))=∫ξ(t)f_1(x,t)dt=e(t)\] 其中\(ξ(t)\)是含有随机变量\(x\)的随机过程，\(f_1(x,t)\)是\(x\)的概率密度函数。
此时随机过程的期望应该是一个关于时间的函数。表示的是随机过程值的摆动中心。

方差

\[D(ξ(t))=E(ξ^2(t))-e(t)^2\] 随机过程的方差表示随机过程值围绕期望的摆动幅度。

自相关函数

随机过程的自相关函数用于描述随机过程在不同时间点上的随机变量之间的关联程度。
\[R(t,t+τ)=E[ξ(t)ξ(t+τ)]\] 自相关函数在\(τ=0\)时取得最大值，易证\(R(0)=E[ξ^2(t)]\)。
自相关函数在通信领域的一个应用是用于判断多径效应产生的时移信号与原信号之间的相关性。

平稳随机过程

严平稳过程要求随机变量的变化与初始值无关，只与时间间隔有关的随机过程。
\[f_n(x_1,...,x_n;t_1,...,t_n)=f_n(x_1,...,x_n;t_1+τ,...,t_n+τ)\] 宽平稳过程要求：
1. 随机过程的均值是一个常数：\(E(ξ(t))=C\) 2. 自相关函数是一个只关于时间间隔\(τ\)的函数：\(R(t,t+τ)=R(τ)\)

功率信号

在通信系统中，功率信号是一个宽平稳随机过程，下面使用自相关函数研究其性质。
> 此处自变量为τ（如平均功率为τ=0）

功率信号	自相关函数	注解
平均功率	\(R(0)=E(ξ^2(t))\)
直流功率	\(R(∞)=E^2(ξ(t))\)	当τ→∞时，表示为两个不相关信号的自相关函数
交流功率	\(R(0)-R(∞)=σ^2\)	平均功率=交流功率+直流功率

求解平均功率的方式：
1. \(R(0)\) 2. \(E(ξ^2(t))\) 3. 谱密度函数的积分 - 对于角频率谱密度函数：\(\frac{1}{2π}∫P_ξ(ω)dω\) - 对于频率密度函数：\(∫P_ξ(f)df\)

由于直流功率（功率的直流分量）是一个常数而不含有任何信息，对信号处理时常常使用自相关函数分解直流功率和交流功率。

遍历随机过程

如果一个随机过程的任何一个样本都经历了平稳随机过程所有的可能状态，称这个随机过程是遍历随机过程（Ergodic Random Process）。遍历随机过程最大的特点是过程中的任意一个随机变量\(x(t)\)的在时间上的统计特性和这个随机过程\(ξ(t)\)的统计特性相等。
对于遍历随机过程的期望：
\[E[ξ(t)]=∫ξf(ξ,t)dt=\lim_{T→∞}\frac{1}{T}∫_{-\frac{T}{2}}^\frac{T}{2}x(t)dt=\overline{a}\] 遍历随机过程的自相关函数：
\[R(τ)=E[ξ(t)ξ(t+τ)]=\lim_{T→∞}\frac{1}{T}∫_{-\frac{T}{2}}^\frac{T}{2}x(t)x(t+τ)dt=\overline{R(τ)}\] 综合上述两点，遍历随机过程必然是平稳随机过程。

证明遍历性

1. 计算过程中任意一个随机变量的期望：\(E(x)=∫xf(t)dt\)
2. 计算随机过程的时间均值：\(\lim_{T→∞}\frac{1}{T}∫_{-\frac{T}{2}}^\frac{T}{2}f(t)dt\)
3. 证明两者相等

对于时间均值函数： \[\overline{f(t)}=\lim_{T→∞}\frac{1}{T}∫_{-\frac{T}{2}}^\frac{T}{2}f(t)dt\] 当\(f(t)\)是一个周期函数时，其时间均值为0。

随机过程通过系统

由于真实的信号和噪声都是随机过程，因此有必要知道对于给定的随机过程，通过系统后，系统的输出情况。
### 随机过程通过线性系统 设系统的单位冲击响应\(h(t)⇔H(ω)\)，当随机过程\(ξ_i(t)\)通过系统后，系统的输出信号为\(ξ_o(t)\)，有：
\[ξ_o(t)=h(t)*ξ_i(t)=∫_0^∞h(τ)ξ_i(t-τ)dτ\] #### 输出信号的期望 \[\begin{aligned} E[ξ_o(t)]&=E[∫_0^∞h(τ)ξ_i(t-τ)dτ]\\ &=∫_0^∞h(τ)dτE[ξ_i(t-τ)]\\ &=∫_0^∞h(τ)dτE[ξ_i(t)]\\ &=H(0)E[ξ_i(t)] \end{aligned}\] 因此当输入信号是一个平稳随机过程，其期望\(E[ξ_i(t)]=a\)时，输出信号的期望：
\[E[ξ_o(t)]=H(0)E[ξ_i(t)]=aH(0)\]

输出信号的自相关函数

\[\begin{aligned} R_o(t,t+τ)&=E[ξ_o(t)ξ_o(t+τ)]\\ &=E[∫_0^∞h(α)ξ_i(t-α)dα∫_0^∞h(β)ξ_i(t+τ-β)dβ]\\ &=∫_0^∞h(α)dα∫_0^∞h(β)dβE[ξ_i(t-α)ξ_i(t+τ-β)]\\ &=∫_0^∞h(α)dα∫_0^∞h(β)dβR_i(τ+α-β)\\ \end{aligned}\] 因此，输出信号的自相关函数结果也必然是一个只与\(τ\)有关的函数：
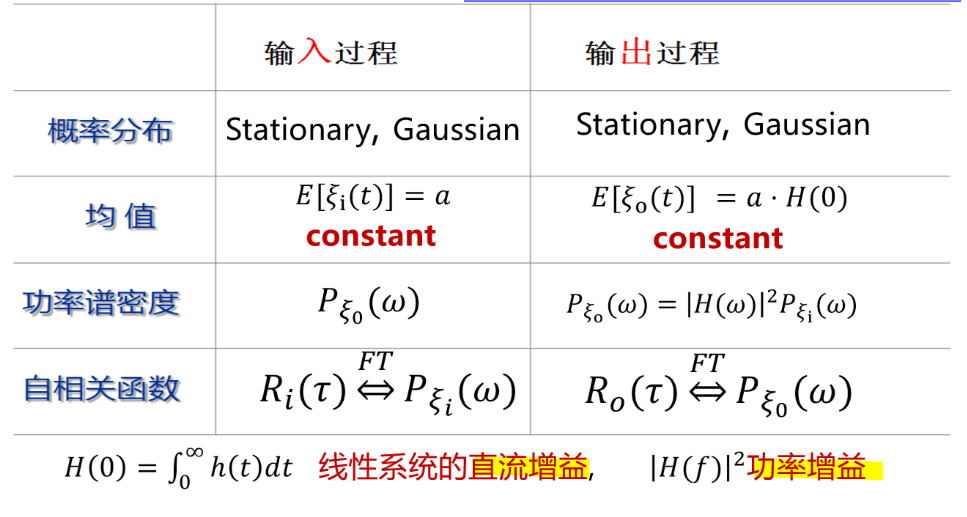
\[R_o(t,t+τ)=∫_0^∞h(α)dα∫_0^∞h(β)dβR_i(τ+α-β)=R_o(τ)\] 综合自相关函数和期望，可以得出结论：如果线性系统的输入信号是一个平稳随机过程，那么输出信号也必然是一个平稳随机过程。

功率谱密度

假设输入信号的功率谱密度为\(P_{ξ_i}(ω)=∫R_i(τ)e^{-jωτ}dτ\)，有：
\[\begin{aligned} P_{ξ_o}(ω)&=∫R_o(τ)dτ\\ &=∫dτ∫_0^∞h(α)dα∫_0^∞h(β)dβR_i(τ+α-β)\\ &=∫_0^∞h(α)e^{jωα}dα∫_0^∞h(β)e^{-jωβ}dβ∫R_i(τ')e^{-jωτ'}dτ'\\ &=H^*(ω)H(ω)P_{ξ_i}(ω)\\ &=|H(ω)|^2P_{ξ_i}(ω) \end{aligned}\]

随机过程通过调制系统

在信号中，调制系统的实质是一个乘法器，将输入信号与一个正弦信号相乘，得到输出信号。

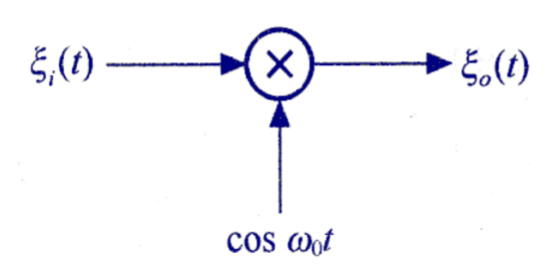
调制系统的输出信号可以表示为：
\[ξ_o(t)=ξ_{i}(t)cosω_0t\] 调制系统是一个非线性系统。

输出信号的自相关函数

\[\begin{aligned} R_o(t,t+τ)&=E[ξ_o(t)ξ_o(t+τ)]\\ &=E[ξ_i(t)ξ_i(t+τ)cosω_0tcosω_0(t+τ)]\\ &=\frac{1}{2}E[ξ_i(t)ξ_i(t+τ)][cosω_0t+cos(2ω_0t+ω_0τ)]\\ &=\frac{1}{2}R_i(τ)[cosω_0t+cos(2ω_0t+ω_0τ)]\\ &=\frac{1}{2}R_i(τ)cosω_0t+\frac{1}{2}R_i(τ)cos(2ω_0t+ω_0τ)\\ \end{aligned}\]

输出信号的功率谱密度

可以发现，由于\(cos(2ω_0t+ω_0τ)\)的存在，输出信号的自相关函数不再是一个只与\(τ\)相关的函数，此时如果要想通过傅里叶变换求到其频谱密度函数非常困难。
此时的方法是选用\(cos(2ω_0t+ω_0τ)\)的时间均值来近似代表其在整个时间上的变化规律。
\[\overline{R_o(t,t+τ)}=\frac{1}{2}R_i(τ)cosω_0t+\frac{1}{2}R_i(τ)\overline{cos(2ω_0t+ω_0τ)}\] 由于\(cos(2ω_0t+ω_0τ)\)是一个周期函数，其时间均值为0。
因此\(\overline{R_o(t,t+τ)}=\frac{1}{2}R_i(τ)cosω_0t\)。
对其做傅里叶变换得到输出信号的功率谱密度函数：
\[P_{ξ_o(ω)}=F[\frac{1}{2}R_i(τ)cosω_0t]=\frac{1}{4}[P_{ξ_i}(ω+ω_0)+P_{ξ_i}(ω-ω_0)]\]