03. 离散时间傅里叶变换

离散时间傅里叶变换

傅里叶变换的意义

对于一个线性时不变系统，系统任意的输入的信号可以表示为一系列特征函数的线性组合。而傅里叶变换的本质在于求出这个线性组合中每一项的系数和这个线性组合本身的表示。而连续时间域中的傅里叶变换是离散域中线性组合概念的拓展。
离散频域中的线性时不变系统的特征函数是指数函数（序列）:\(e^{jω_kn}\)，因此通过傅里叶变换，任何一个满足狄利克雷条件的离散时间域中的信号都可以表示为指数序列的线性组合：
\[x[n]=∑_ka_ke^{jω_kn}\] 通过傅里叶变换，这个线性组合可以表示为： \[x[n]=\frac{1}{2π}∫_{-π}^πX(e^{jω})e^{jωn}\] 其中\(X(jω)\)为这个线性组合的系数，有：
\[X(e^{jω})=∑_{n=-∞}^∞x[n]e^{-jωn}\] 上述式子称为离散时间傅里叶变换。 > 由于等比数列的求和性质，变换的结果是一个连续频谱。

其反变换即线性组合的表达式:
\[x[n]=\frac{1}{2π}∫_{-π}^πX(e^{jω})e^{jωn}\]

由傅里叶变换，这个线性组合的特征函数\(e^{jωn}\)在时域内表现为正弦函数\(cosωn\)，因此这个线性组合在时域上表征为正弦函数的线性组合，这表示一个信号可以被分解为若干个特性不同的正弦波。

连续和离散时间傅里叶变换的对比如下表所示：

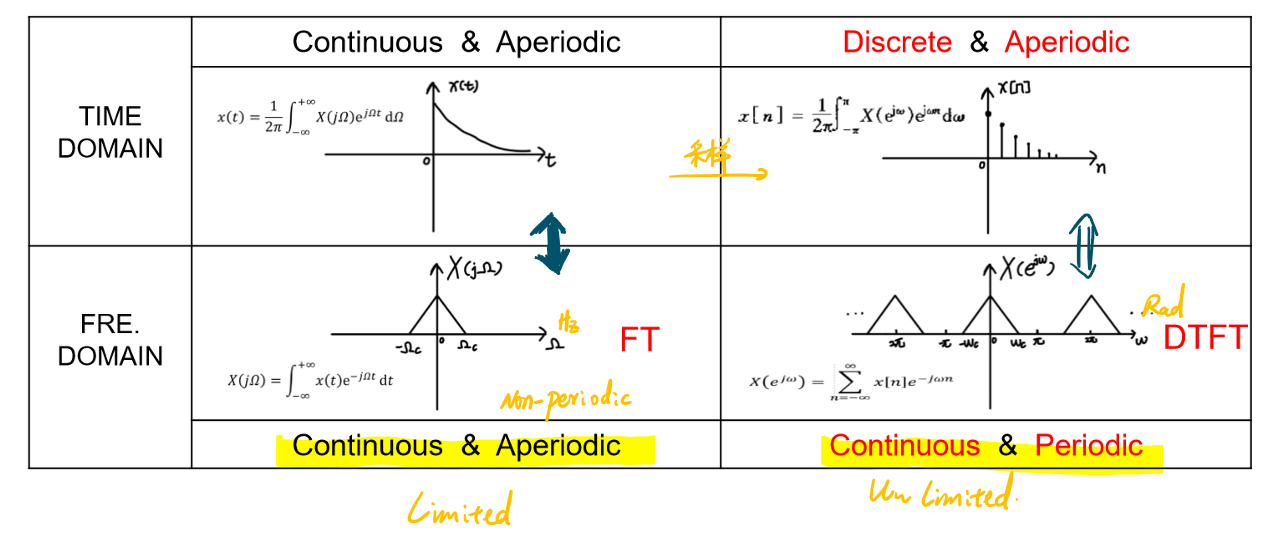
离散时间傅里叶变换的共轭性质

序列的分解

复分解

同连续傅里叶变换，离散时间傅里叶变换也可以做复分解：
\[X(e^{jω})=X_R(e^{jω})+jX_I(e^{jω})\] #### 共轭分解 定义序列\(x[n]\)的共轭对称序列:
\[x_e[n]=\frac{1}{2}(x[n]+x^*[-n])\] 共轭对称序列的性质：\(x_e[n]=x_e^*[-n]\)
序列\(x[n]\)的共轭反对称序列:
\[x_o[n]=\frac{1}{2}(x[n]-x^*[-n])\] 共轭反对称序列的性质：\(x_o[n]=-x_o^*[-n]\)
任何一个序列\(x[n]\)可以表示为其共轭对称和共轭反对称序列的和：
\[x[n]=x_e[n]+x_o[n]\] 共轭分解对频域序列也同样适用。

共轭信号的性质

注解	时域序列	频域变换
反向	\(x^\*[n]\) \(x^\*[-n]\)	\(X^\*(e^{-jω})\) \(X^\*(e^{jω})\)
幅度分量为偶函数	\(\lvert X(e^{jω})\rvert\)	\(\lvert X(e^{-jω}) \rvert\)
相位分量为奇函数	\(∠X(e^{jω})\)	\(-∠X(e^{-jω})\)
实部分量为偶函数	\(X_R(e^{jω})\)	\(X_R(e^{-jω})\)
虚部分量为奇函数	\(X_I(e^{jω})\)	\(-X_I(e^{-jω})\)

离散时间傅里叶变换的性质

注解	时域序列	频域变换
线性	\(ax[n]+by[n]\)	\(aX(e^{jω})+bY(e^{jω})\)
时移	\(x[n-n_0]\)	\(e^{-jωn_0}X(e^{jω})\)
频移	\(e^{jω_0n}x[n]\)	\(X(e^{j(ω-ω_0)})\)
反转	\(x[-n]\)	\(X(e^{-jω})\)
频域微分	\(nx[n]\)	\(j\frac{dX(e^{jω})}{dω}\)

卷积特性

时域卷积：
\[x[n]*y[n]⇔X(e^{jω})Y(e^{jω})\] 频域卷积：
\[x[n]y[n]⇔\frac{1}{2π}X(e^{jω})*Y(e^{jω})=\frac{1}{2π}∫_{-π}^πX(e^{jθ})Y(e^{j(ω-θ)dθ})\]