04. Z变换

Z变换

离散傅里叶变换的局限性

对于离散傅里叶变换\(X(e^{jω})=∑x[n]e^{-jωn}\)，要求原离散信号\(x(n)\)满足狄利克雷条件，即要求变换中的求和项收敛：
\[∑|x[n]|<∞ \] 有大量的信号不能满足这一条件。

Z变换原理

解决办法是在变换时添加一项\(r^{-n}\)，以在保留原信号特征的同时改善原信号的收敛性。 \[X_r(e^{jω})=∑x[n]r^{-n}e^{-jωn}=∑x[n](re^{jω})^{-n}\] 将：\(re^{jω}\)简记为\(z\)，得到Z变换的变换公式：
\[X(z)=∑x[n]z^{-n}\] Z变换可以将输入序列转变为以指数序列构成的线性组合。
### 收敛域 此时要求改善后的信号满足狄利克雷条件，有：
\[∑|x[n]z^{-n}|<∞\] 满足这个条件的\(z\)的取值称为这个Z变换对的收敛域。
可以发现\(|z|\)的取值决定了整个线性组合是否满足狄利克雷条件。
当\(|z|=1\)时，Z变换退化为离散傅里叶变换，满足这一条件的所有\(ω\)的取值在傅里叶平面内构成一个单位圆：

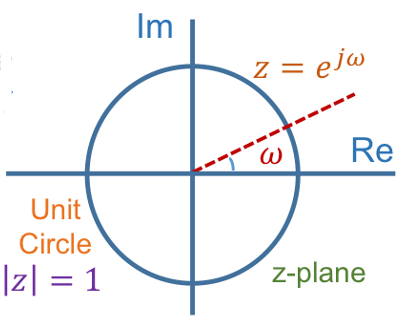
收敛特性

序列的Z变换是否存在与收敛域有关，下面讨论不同类型序列的收敛域特征：

序列类型	收敛域	图示
右边序列：\(x[n]=a^nu[n]\)	\(‖z‖>‖a‖\)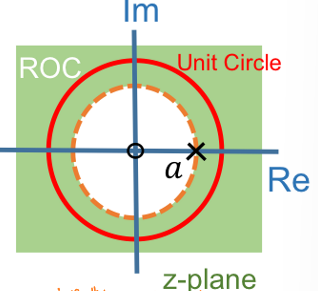
左边序列：\(x[n]=-a^nu[-n-1]\)	\(‖z‖<‖a‖\)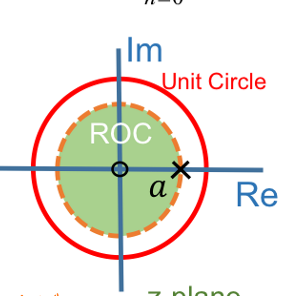
双边序列:\(x[n]=a^nu[n]-b^nu[-n-1]\)	\(‖a‖<‖z‖<‖b‖\)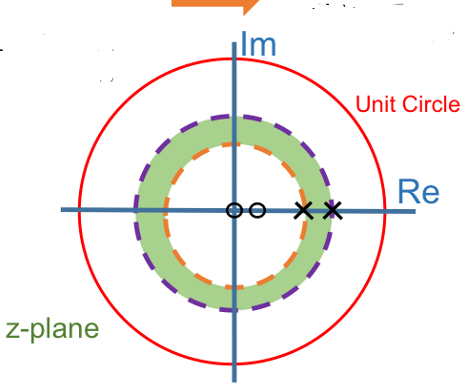

由上表可以总结出Z变换的三条性质： 1. 当且仅当收敛域包括单位圆时，原信号才能同时满足稳定性和因果性，其离散傅里叶变换存在。
2. 收敛域以极点（指数序列的基底）、0、无穷划分边界。
3. 在收敛域内不存在任何极点。

Z反变换

定义式

定义Z反变换为：
\[x[n]=\frac{1}{2πj}∮_{ROC}X(z)z^{n-1}dz\] 反变换的定义式涉及到曲线积分、计算比较困难，由于LIT系统的系统方程都能够写作多项式分数的形式，因此对LIT系统方程而言通常不采用求解定义式的方式来求解反变换，而更多地采用如下方法求解反变换式：

Z变换式的部分分式形式

序列\(x(n)\)的z变换式\(X(z)\)的一般形式可以写作由两个多项式组成的分式，称为部分分式：
\[X(z)=\frac{N(z)}{D(z)}=\frac{∑b_mz^m}{∑a_nz^n}\] 其中\(b_m\)称为方程的零点，\(a_m\)称为方程的极点。
当极点为一阶时,对等式两边同时除以\(z\)以提取常系数\(A\)：
\[\frac{X(z)}{z}=∑_{i=1}^N\frac{A_i}{z-a_i}\] 其中\(A_i=(z-a_i)\frac{X(z)}{z}|_{z=a_i}\)。
再乘上\(z\)：
\[X(z)=∑_{i=1}^N\frac{A_iz}{z-a_i}\] 其中\(A_i\)为\(x(n)\)的常系数，\(a_i\)为底数，也是极点。 对应的\(x(n)\)： \[x(n)=∑_{i=0}^∞A_i(a_i)^nu[n],n≥0\]

需要注意的是，需要根据\(z-a_i\)的正负对Z变换的收敛域进行讨论:
- 当\(|z|<(a_i)_{min}\)时，根据极点对应序列形式（收敛特性一小节中提到的表格），该项对应的指数序列为左边序列\(-A_i(a_i)^nu[-n-1]\)。对应分式项\(\frac{A_iz}{z-a_i}\)应写作\(-\frac{A_iz}{z-a_i}\)以保证\(z-a_i\)恒正。
- 当\(|z|>(a_i)_{max}\)时，根据极点对应序列形式，该项对应的指数序列为右边序列\(A_i(a_i)^nu[n]\)。 对应分式项应写作\(\frac{A_iz}{z-a_i}\)以保证\(z-a_i\)恒正。
- 当\(a_{min}<|z|<a_{max}\)时，根据极点对应序列形式，该项对应的指数序列为双边序列。

离散系统的频率响应与传递函数

离散系统的差分方程可以写作：
\[∑_{k=0}^Na_ky[n-k]=∑_{k=0}^Mb_kx[n-k]\] 求得系统的传递函数为：
\[H(z)=\frac{Y(z)}{X(z)}=\frac{∑b_mz^m}{∑a_nz^n}\] 定义系统的频率响应为输入和输出的离散时间傅里叶变换结果之比：
\[H(e^{jω})=\frac{Y(e^{jω})}{X(e^{jω})}\] 当系统的极点在单位圆内，且零点没有限制时,Z变换和离散时间傅里叶变换存在如下关系：
\[H(z)|_{z=e^{jω}}=H(e^{jω})\] 即\(z=e^{jω}\)。 带入频率响应，得到：
\[H(e^{jω})=\frac{b_0}{a_0}\frac{e^{jω(N-M)}Π_{k=1}^M(e^{jω}-b_k)}{Π_{k=1}^N(e^{jω}-a_k)}\] 可以发现\(e^{jω}-b_k\)和\(e^{jω}-a_k\)都表示从点\((b_k,0)\)或\((a_k,0)\)到单位圆上一点的向量。

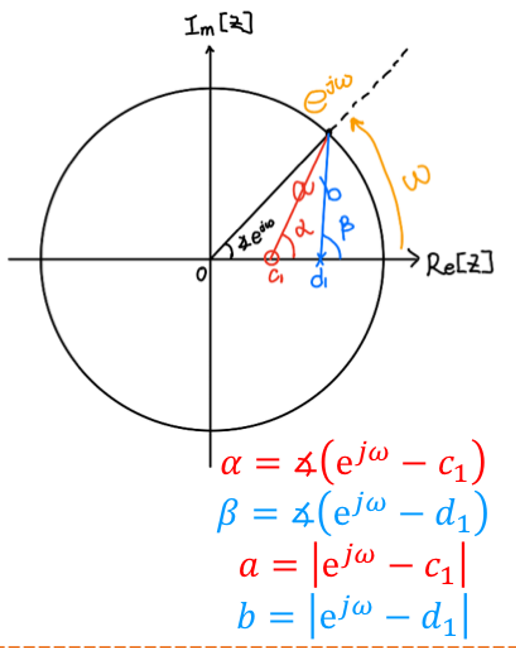
将系统的频率响应转化为角度表示：\(H(e^{jω})=|H(e^{jω})|e^{∠H(e^{jω})}\)，有：

• 系统方程的模长/幅度值(Magnitude)：
  \[|H(e^{jω})|=\frac{Π零向量的模长}{Π极向量的模长}\] 即系统方程频率响应\(H(e^{jω})\)的幅度值-频率响应，简称幅频响应。
  
• 系统方程的相位：
  \[∠H(e^{jω})=∑零向量的角度-∑极向量的角度\] 即系统方程频率响应\(H(e^{jω})\)的相位-频率响应，简称相频响应。