02. 滤波器
本文最后更新于 2025年6月4日 晚上
滤波器
滤波器按照滤波器本身是否消耗额外的能量(由于需要额外提供能量的组件多为运算放大器,因此也可按照有无运算放大器参与滤波分类)分为无源滤波器(额外不消耗能量、无运算放大器)和有源滤波器(额外消耗能量、有运算放大器)。
滤波器的阶数由滤波元件(L.C)的个数决定,在实际电路中,由于电感的体积较大,在集成电路设计中通常使用电容作为滤波元件。
无源滤波器
无源滤波器的截止频率由\(X_c=R\)给出:
\[f_c=\frac{1}{2πRC}\]
一阶低通滤波器
电路图如下所示:
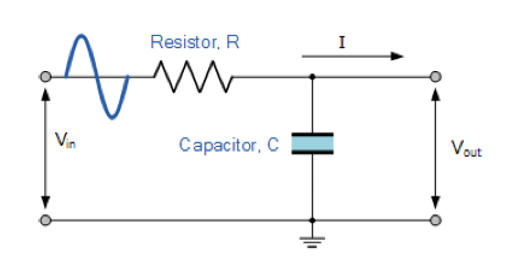
当电压信号频率增大时,电容容抗减小最终导致电容短路,\(V_{out}=0\)。
当电压信号频率减小时,电容容抗增大最终导致电容断路,此时\(V_{out}\)是有数值的。
一阶低通滤波器的频率响应特性如下图所示:
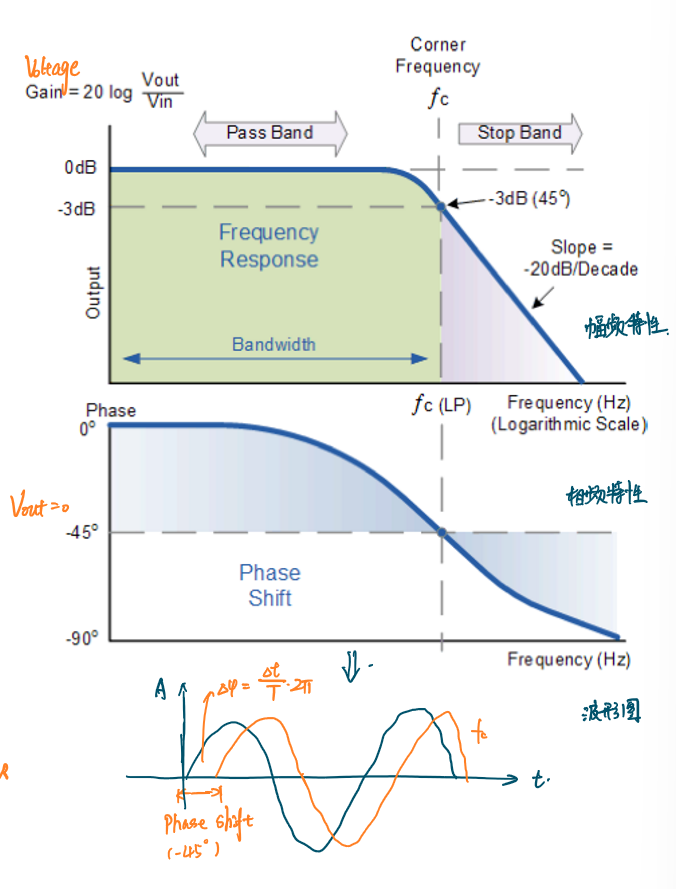
相移规律如下:
\[φ=-arctan(\frac{R}{X_c})=-arctan(2πfRC)\] 当达到滤波器的截止频率时:\(X_c=R\),因此相位移动为-45°。
二阶低通滤波器
由于无源滤波器都是线性滤波器,因此其特性实际上是一阶滤波器的线性叠加。
二阶无源低通滤波器的电路如图所示:
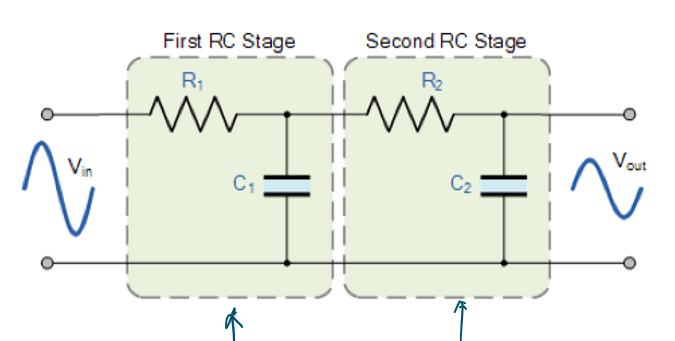
二阶低通滤波器的截止频率:
\[f_c=\frac{1}{2π√(R_1R_2C_1C_2)}\] 其频率响应特性如下图所示:
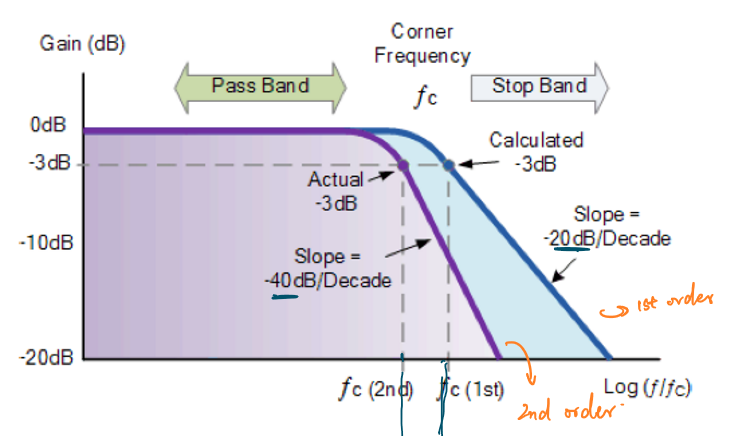
其相移为两个一阶滤波器的相移之和,即: \[φ=φ_1+φ_2\] 因此当滤波器达到截止频率时,其相移为-90°。
一阶高通滤波器
一阶高通滤波器的电路图与一阶低通滤波器的电路图相同,只是被测目标由电容改为了电阻。因此截止频率与一阶低通滤波器相同。
一阶高通滤波器的频率响应特性如图所示:
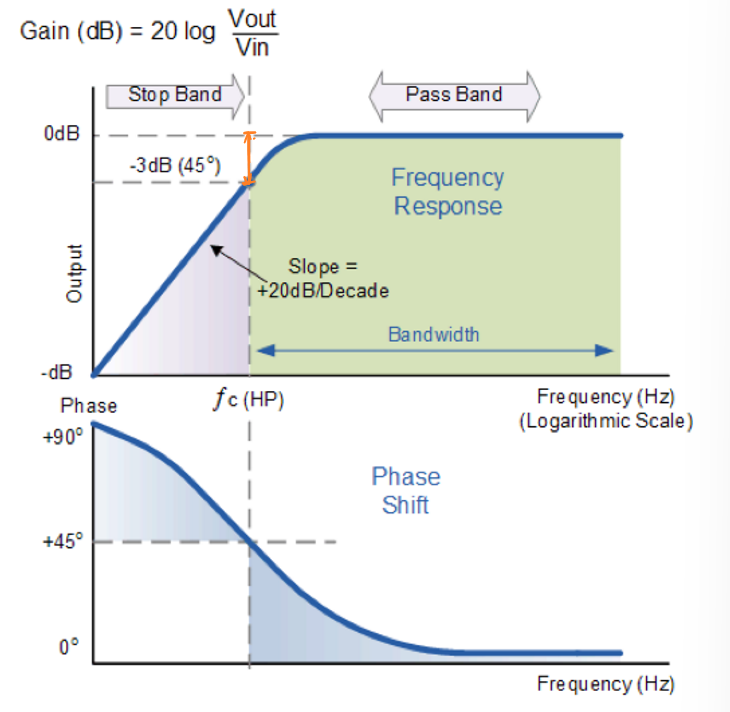
相移规律如下:
\[φ=arctan(\frac{R}{X_c})=arctan(2πfRC)\] 当达到滤波器的截止频率时:\(X_c=R\),因此相位移动为45°。
二阶高通滤波器
二阶高通滤波器的电路图如图所示:
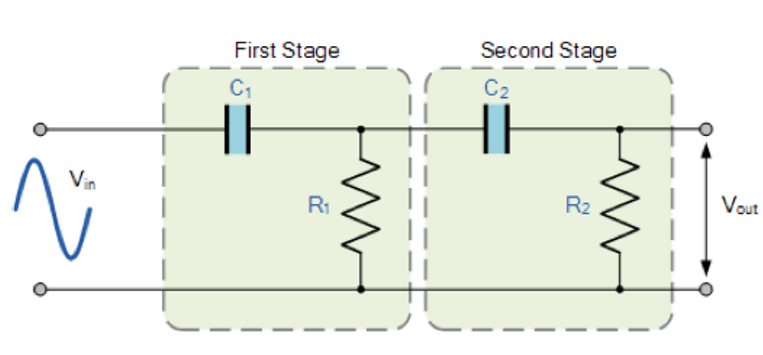
其频率响应特性图如图所示:
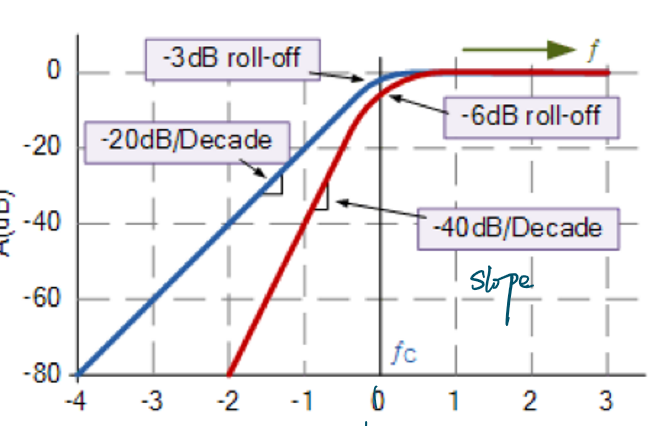
因此当滤波器达到截止频率时,其相移为90°
带通滤波器
带通滤波器的电路图为一个高通滤波器与一个低通滤波器并联。
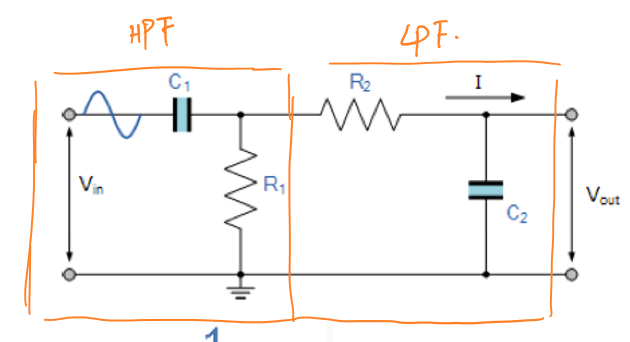
其频率响应图如图所示:
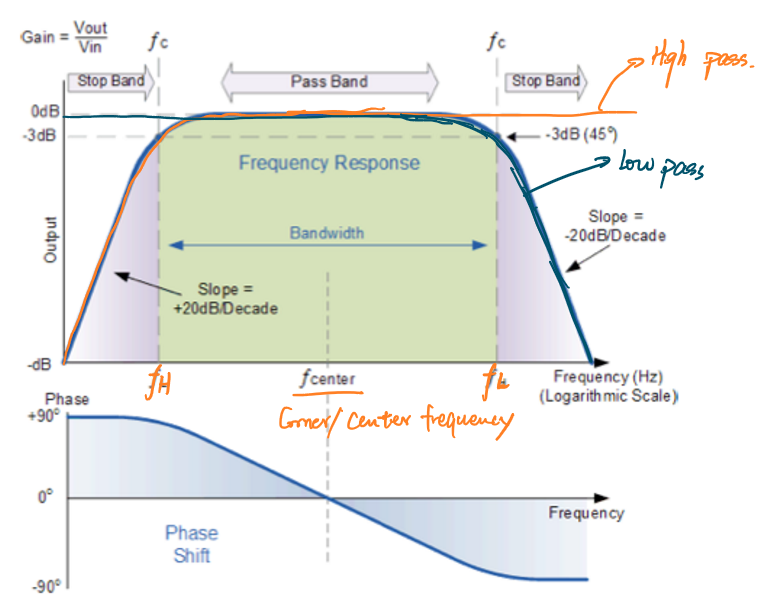
对于带通滤波器,其拥有两个截止频率\(f_H\)和\(f_L\),分别对应高通滤波器和低通滤波器的截止频率。
\[f_H=\frac{1}{2πR_1C_1},f_L=\frac{1}{2πR_2C_2}\] > 注意\(f_H<f_L\)。
其中心响应频率(Central resonance frequency)是这两个截止频率乘积的平方根:
\[f_c=√f_L×f_H=\frac{1}{2π√(R_1R_2C_1C_2)}\] 带通滤波器的相移在达到中心响应频率时为0。
定义带通滤波器的品质因数\(Q\):
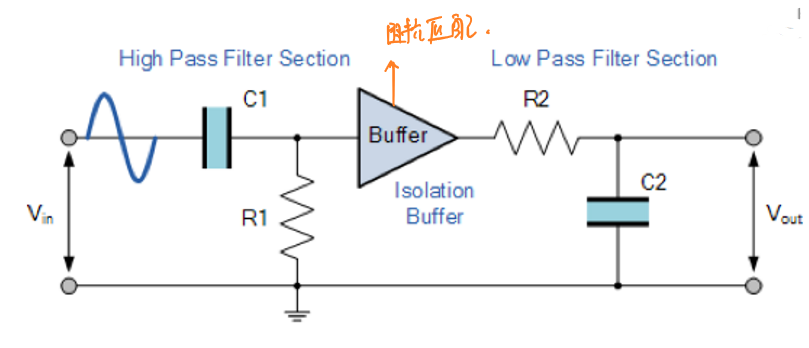
\[Q=\frac{f_c}{BW}=\frac{f_c}{f_H-f_L}\] 有时候为了彻底阻隔高通滤波器和低通滤波器之间的相互影响,会在分流处放置一个缓冲器,如图所示:
| 名称 | 电路图 | 被测目标 | 截止频率 | 下降/上升斜率 | 达到截止频率时的相移 |
|---|---|---|---|---|---|
| 一阶低通滤波器 |  |
C | \(\frac{1}{2πRC}\) | -20dB | -45° |
| 一阶高通滤波器 | 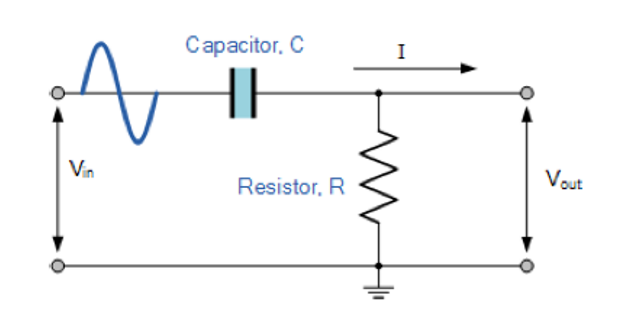 |
R | \(\frac{1}{2πRC}\) | 20dB | 45° |
| 二阶低通滤波器 |  |
C | \(\frac{1}{2π√(R_1R_2C_1C_2)}\) | -40dB | -90° |
| 二阶高通滤波器 |  |
R | \(\frac{1}{2π√(R_1R_2C_1C_2)}\) | 40dB | 90° |
| 带通滤波器 |  |
R、C | \(f_r=\frac{1}{2π√(R_1R_2C_1C_2)}\) \(f_H=\frac{1}{2πR_1C_1}\) \(f_L=\frac{1}{2πR_2C_2}\) |
20dB -20dB |
0° 90° -90° |
有源滤波器
有源滤波器中含有运算放大器,因此其最大增益必定大于0dB。
简单的有源滤波器电路实质是无源滤波器的输出端与运算放大器电路的输入端连接得到的电路,加入运算放大器的好处有两点:
- 由于理想运算放大器内部输入阻抗远大于输出阻抗,因此在输出端运算放大器可以提供低的输出阻抗。
- 激励电压信号/电流,减少信号在传输过程中的损失。
由于无源滤波器电路和运算放大器电路相互独立,因此有源滤波器的截止频率,上升速率等性质仍然与无源滤波器相同。
与无源滤波器不同的是,此时的最大增益不再为0dB,而是按照正相/反相运算放大器提供的最大增益进行计算。
有源滤波器的电路分析要点
- 对于高阶滤波器,从无源滤波器入手,观察电流的分流点。
- 找到每个无源滤波器与放大器输入端连接的节点,假设信号频率升高或者降低,观察此点的电压变化,由此判断出滤波器的类型(高通/低通)和放大器(正相/反相)的类型。
- 根据滤波器输出电压判断滤波器类型和放大器类型,进行相应的计算。
有源带通滤波器
有源带通滤波器的结构为一个高通滤波器和低通滤波器分别跨在一个放大器的两侧串联构成,如图所示:
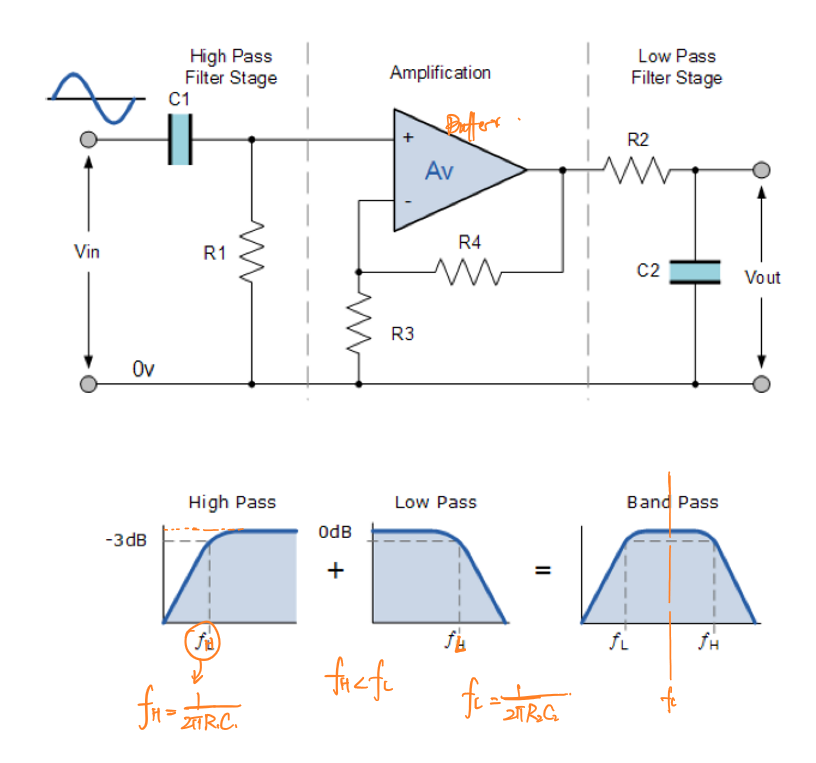
简化后的有源带通滤波器电路:
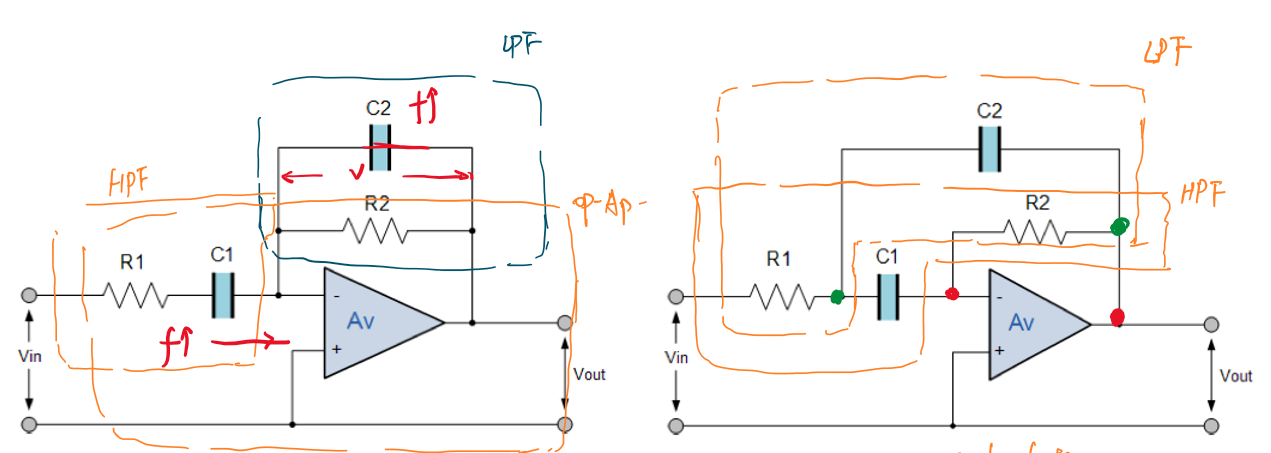
有源带阻滤波器
有源带阻滤波器由带通滤波器由低通和高通滤波器与放大器并联得到:
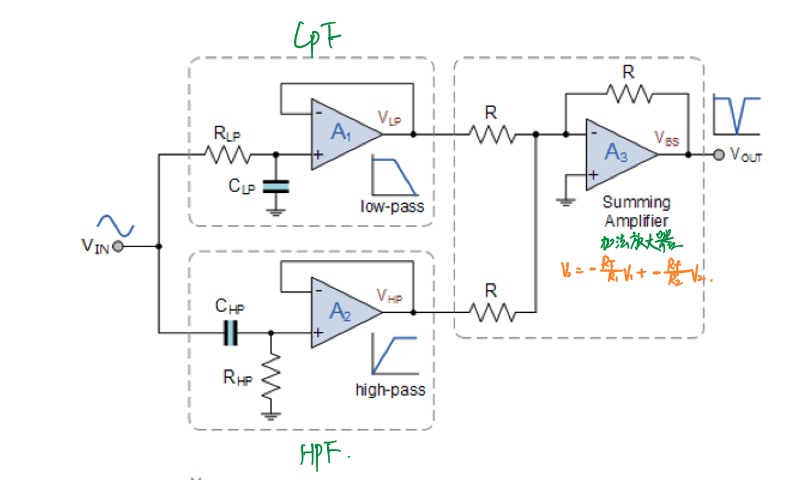
带阻滤波器的计算方法和带通滤波器完全相同,其各参数为各无源滤波器参数的线性叠加。带阻滤波器的中心响应频率为:
\[f_c=√f_L×f_H\] 达到中心响应频率时,同带通滤波器,其相移为0°。
带阻滤波器的品质因数计算方法和带通滤波器完全相同。
陷波滤波器
陷波滤波器(Notch Filter)是带阻滤波器的一种,由于陷波滤波器的\(f_L\)和\(f_H\)相隔很近,其阻带很窄,因此也称点阻滤波器。常常用于去除固定频率分量或阻带很窄的地方。如用于去除直流分量,去除某些特定频率分量。
陷波滤波器的电路图和带阻滤波器完全相同,其频率响应特性如图所示:
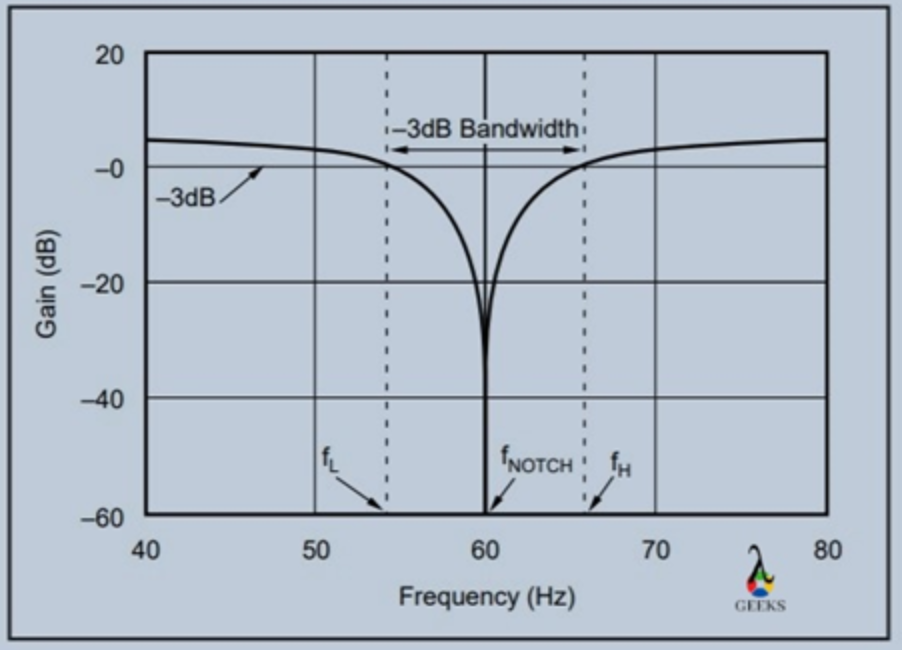
陷波器的中心响应频率记作\(f_N\),计算方法同带阻滤波器。
> 陷波器的相关资料:https://zh-cn.lambdageeks.com/notch-filter-circuit/#def
Sallen-Key 滤波器结构(二阶高通滤波器)
Sallen-Key滤波器是一种滤波器的搭建结构。其二阶高通滤波器的基本结构如图所示:
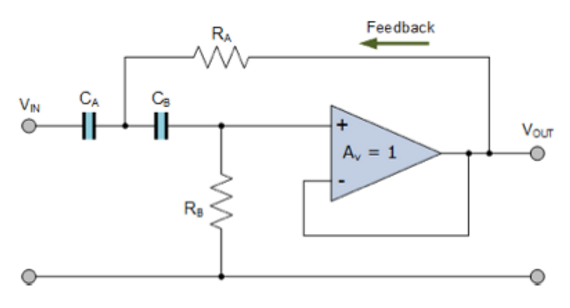
这种构造的滤波器可以通过直接改变运算放大器的增益来改变整个滤波器的最大增益,滤波器的最大增益由如下公式给出:
\[Gain_{max}=A×Q\] 其中\(A\)表示运算放大器的增益。
该放大器的中心响应频率为:
\[f_C=\frac{1}{2π√R_AR_BC_AC_B}\] 通常所有电阻的阻值相等,所有电容的电容值相等:
\[f_C=\frac{1}{2πRC}\] Sallen-Key 滤波器的品质因数由如下公式给出:
\[Q=\frac{1}{3-A}\] > Sallen-Key滤波器的带宽为3dB。
其频率响应曲线由品质因数\(Q\)决定:
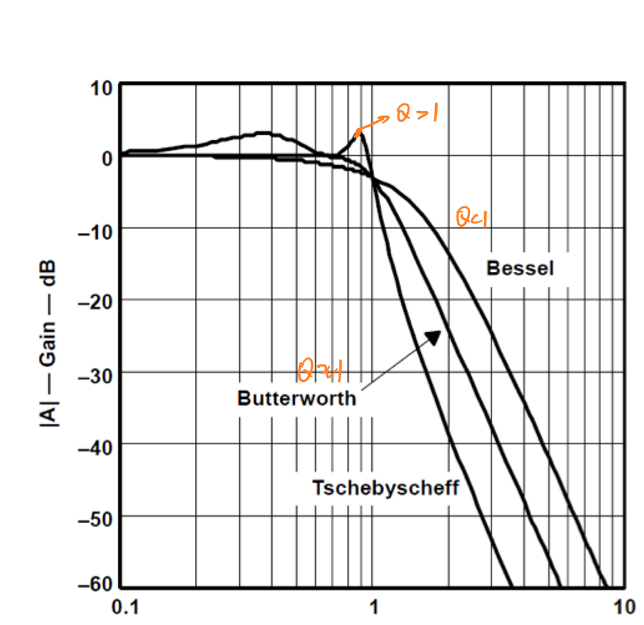
按照\(f = f_0\)附近频率特性的特点,可将滤波器分为巴特沃斯(Butterworth)、切比雪夫(Chebyshev)和贝塞尔(Bessel)三种类型。 > https://www.eet-china.com/mp/a25110.html