05. 离散傅里叶级数·离散傅里叶变换

离散傅里叶级数·离散傅里叶变换

复指数序列的周期性

\(x[n]=e^{jω_0n}\)，由于\(ω_0∈[0,2π)\)的周期性，因此有：\(x[n]=e^{jω_0n}=e^{j(ω_0+2πk)n}\)，令\(ω_0N=2πk,k∈Z\)，有：
\[x[n]=e^{jω_0n}=e^{j(ω_0+2πk)n}=x[n+N]\] 复指数序列\(x[n]\)具有周期性，称\(N\)为其周期。
由于\(ω_k=\frac{2πk}{N}∈[0,2π)\)，因此当序列周期为\(N\)时，当且仅当\(k=0,1,2,...,N-1\)时存在\(N\)个不同的\(ω_k\)。\(N=\frac{2πk}{ω_0}\)。

离散傅里叶级数（DFS）

根据连续时间周期信号的傅里叶变换：
\[x(t)=∑_{k=-∞}^∞X(kΩ_0)e^{jkΩ_0t}\] 其中连续信号的角频率为：\(Ω_0=\frac{2π}{T}\)
类比连续时间周期信号，设周期序列\(\tilde{x}[n]\):\(\tilde{x}[n]=\tilde{x}[n+rN],r∈Z\)，有：
\[\tilde{x}[n]=∑_{k=-∞}^∞X(kΩ_0)e^{j\frac{2π}{N}kn}\] 由于满足条件的频率分量\(ω_k\)只有\(N\)个：
\[\begin{aligned} \tilde{x}[n]&=∑_{k=-∞}^∞X(kΩ_0)e^{j\frac{2π}{N}kn}\\ &=∑_{k=0}^{N-1}X(kΩ_0)e^{j\frac{2π}{N}kn}\\ &=\frac{1}{N}∑_{k=0}^{N-1}\tilde{X}[k]e^{j\frac{2π}{N}kn} \end{aligned}\] 其中\(\tilde{X}[k]\)为离散傅里叶级数系数，可反推得到：
\[\tilde{X}[k]=∑_{n=0}^{N-1}\tilde{x}[n]e^{-j\frac{2π}{N}kn}\]

定义\(W_N^{kn}=e^{-j(\frac{2π}{N})kn}\)，有离散傅里叶级数分析：
\[\tilde{X}[k]=∑_{n=0}^{N-1}\tilde{x}[n]W_N^{kn}\] 离散傅里叶级数合成：
\[\tilde{x}[n]=\frac{1}{N}∑_{k=0}^{N-1}\tilde{X}[k]W_N^{-kn}\]

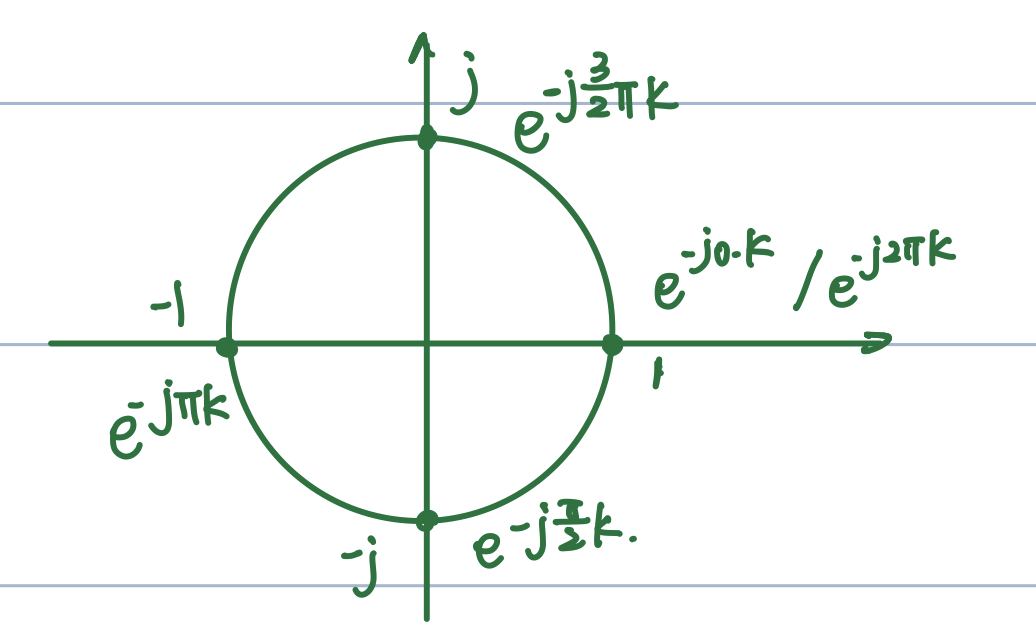
\(W_N^{kn}\)是复数的角度表示形式，一般计算时转化为z域中的坐标以方便计算。如:\(W_4^2=e^{-j\frac{2π}{4}×2}=-1\)

离散傅里叶级数的意义

周期为\(N\)的序列可以表示为\(N\)个周期为\(N\)的复指数序列的线性组合。
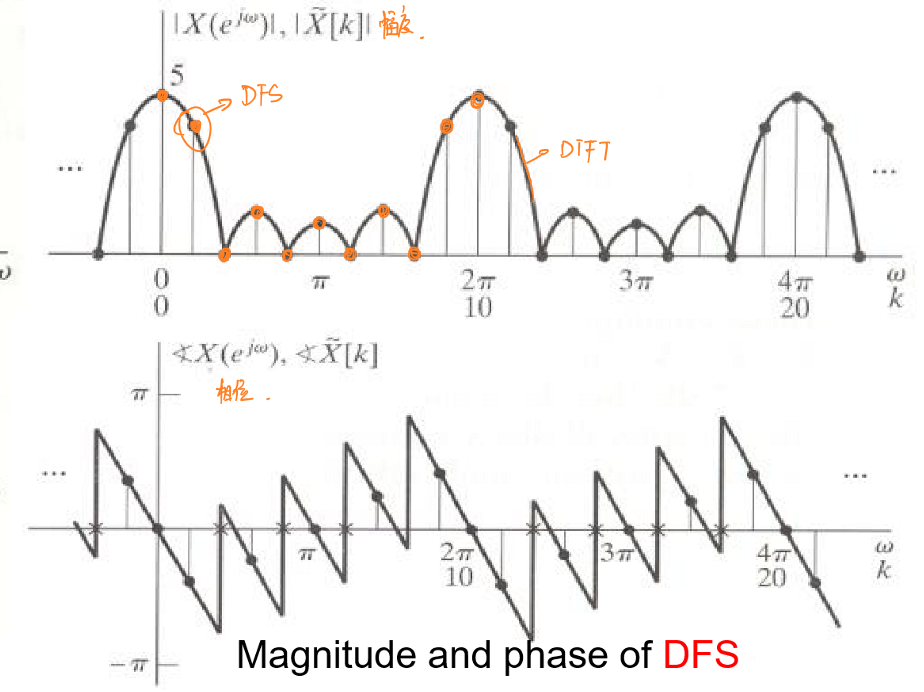
#### 离散傅里叶级数与离散时间傅里叶变换（DTFT）的关系 事实上，可以将离散傅里叶级数看作是对离散时间傅里叶变换结果\(X(e^{jω})\)以周期为\(N\)做延拓后，对其进行采样的结果。

离散傅里叶级数与Z变换的关系

给定Z变换：\(X(z)|_{z=e^{jω}}=X(e^{jω})\)，那么：
\[\tilde{X}[k]=X(z)|_{z=e^{j(2π/N)k}}=X(e^{j(2π/N)k}),k=0,1,...,N-1\] 即离散傅里叶级数可以看做是在Z变换的单位圆上做均匀采样的结果。

离散傅里叶级数的性质

1. 周期性：如果\(\tilde{x}[n]\)的周期为\(N\)，\(\tilde{X}[k]\)的周期同样为\(N\)。
   
2. 线性：\(a\tilde{x_1}[n]+b\tilde{x_2}[n]↔a\tilde{X_1}[k]+b\tilde{X_2}[k]\)
   
3. 时移：\(\tilde{x}[n-m]↔W^{km}_N\tilde{X}[k]\)
   
4. 频移：\(\tilde{X}[k-l]↔W^{-nl}_N\tilde{x}[n]\)
   
5. 对偶性：如果\(\tilde{x}[n]↔\tilde{X}[k]\)，那么\(\tilde{X}[n]↔N\tilde{x}[-k]\)

周期卷积

如果两个序列\(\tilde{x_1}[n]\)、\(\tilde{x_2}[n]\)有相同的周期\(N\)，有: \[\tilde{x_1}[n]\tilde{⊗}\tilde{x_2}[n]=∑_{m=0}^{N-1}\tilde{x_1}[m]\tilde{x_2}[n-m]↔\tilde{X_1}[k]\tilde{X_2}[k]\] 周期卷积定理可以被矩阵化为：
\[\tilde{x}[n]\tilde{⊗}\tilde{y}[n]=\left[\begin{matrix} \tilde{z}[0] \\ \tilde{z}[1] \\ ...\\ \tilde{z}[N-2] \\ \tilde{z}[N-1] \end{matrix}\right]|_{periodic}=\left[\begin{matrix} \tilde{y}[0] & \tilde{y}[N-1] & ...& \tilde{y}[2] & \tilde{y}[1]\\ \tilde{y}[1] & \tilde{y}[0] & ...& \tilde{y}[3] & \tilde{y}[2]\\ ...&...&...&...&...\\ \tilde{y}[N-2] & \tilde{y}[N-1] & ...& \tilde{y}[0] & \tilde{y}[N-1]\\ \tilde{y}[N-1] & \tilde{y}[N-2] & ...& \tilde{y}[1] & \tilde{y}[0]\\ \end{matrix}\right]\left[\begin{matrix} \tilde{x}[0] \\ \tilde{x}[1] \\ ...\\ \tilde{x}[N-2] \\ \tilde{x}[N-1] \end{matrix}\right]\] 可以发现矩阵\(Y\)内部每一列的元素在进行周期性的位置轮换。
周期卷积计算可以在MATLAB®中使用命令toeplitz(x,y)得到，其中x,y为两个周期序列单周期内所有元素组成的向量，两个向量长度相同。
> 当两向量长度不等时，使用0进行补齐。

离散傅里叶变换（DFT）

当离散傅里叶序列变换的对象变成非周期有限长度序列时，此时的变换称为离散傅里叶变换（DFT）：
\[X[k]=∑_{n=0}^{N-1}x[n]W_N^{kn},0≤n≤N-1\] 其反变换为：
\[x[n]=\frac{1}{N}∑_{k=0}^{N-1}X[k]W_N^{-kn},0≤n≤N-1\]

离散傅里叶变换的性质

1. 线性：\(a{x_1}[n]+b{x_2}[n]↔a{X_1}[k]+b{X_2}[k],0≤k≤N-1\)
   
2. 对偶性:如果\({x}[n]↔{X}[k]\)，那么\(\tilde{X}[n]↔N{x}[(-k)mod(N)],0≤k≤N-1\)
3. \(N\)点循环时移：\(x[(n-m)mod(N)]↔W^{km}_NX[k],0≤k≤N-1\)

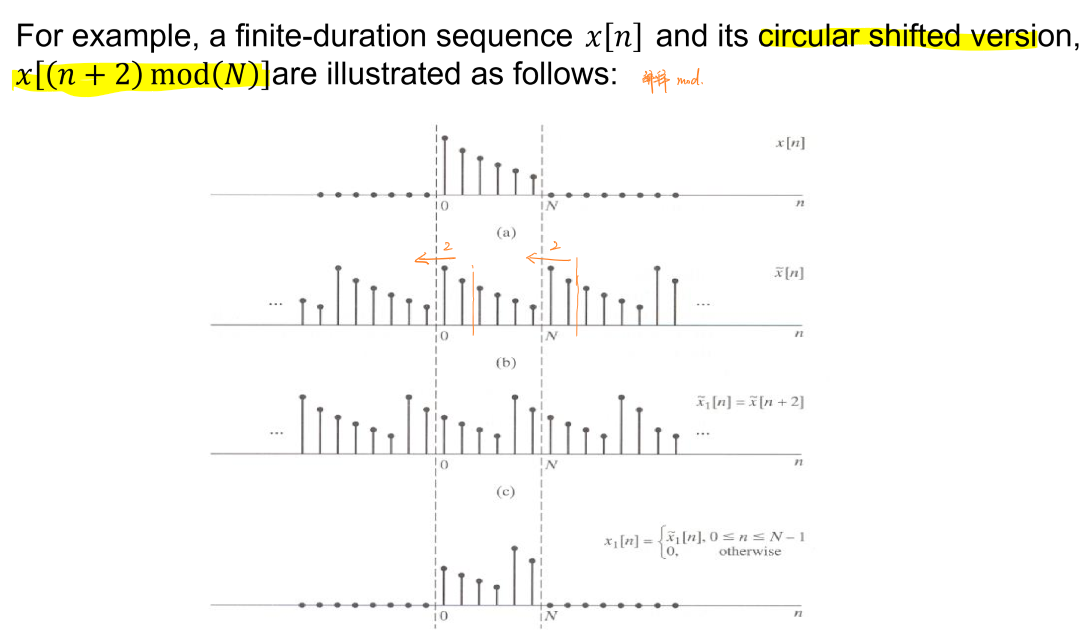
\((n+m)modN\)运算的含义是取序列的\(0-N\)部分以\(N\)为周期进行延拓，延拓后的序列向左平移\(m\)个单位，取现在序列\(0-N\)的结果。

离散傅里叶变换(DFT)、离散傅里叶级数（DFS）、离散时间傅里叶变换（DTFT）、Z变换的关系

不难看出周期序列\(\tilde{x}[n]\)做傅里叶级数分析后一周期内（\(0≤n≤N-1\)）的结果与\(x[n]\)做离散傅里叶变换的结果完全一致。

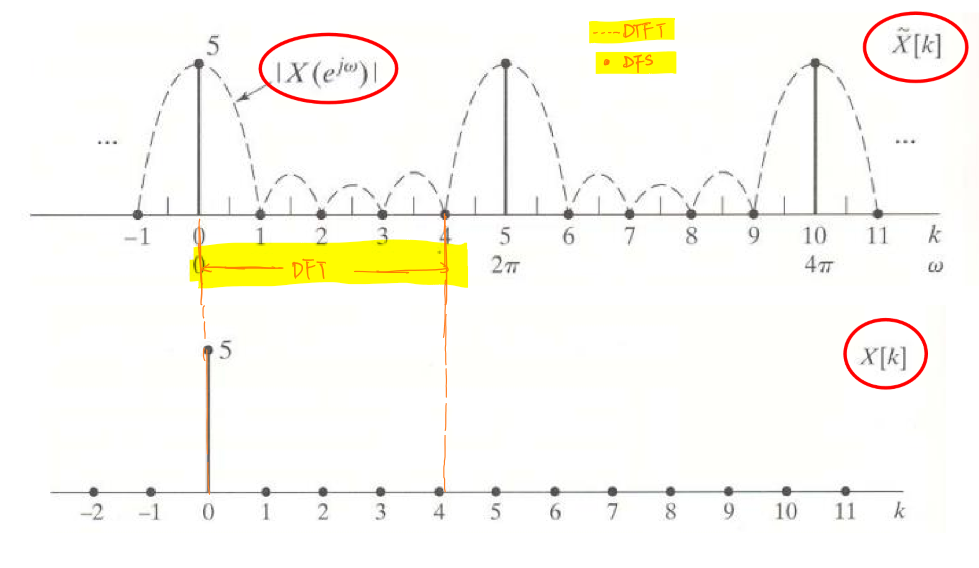
可以发现：离散傅里叶级数是对离散时间傅里叶变换的结果进行采样，而一周期内的采样结果则为离散傅里叶变换的结果。
周期序列\(\tilde{x}[n]\)做傅里叶级数分析后一周期内（\(0≤n≤N-1\)）的结果与\(x[n]\)做离散傅里叶变换的结果完全一致。

可以发现：离散傅里叶级数是对离散时间傅里叶变换的结果进行采样，而一周期内的采样结果则为离散傅里叶变换的结果。
对于Z变换，\(z=re^{jω}\)，如果选择\(r=1\)，那么Z变换将退化为离散时间傅里叶变换：
\[X(e^{jω})=X(z)|_{z=e^{jω}}\] 因此，Z域单位圆上的任意一点表示\(e^{jω}\)。 而离散傅里叶变换是对离散时间傅里叶变换一周期内的采样，因此离散傅里叶变换是在Z域单位圆上的均匀采样。

循环卷积/圆周卷积

定义两个序列非周期序列的\(N\)点\(x[n]\)、\(y[n]\)循环卷积/圆周卷积（Circular shift）为：
\[x[n]⊗_Ny[n]=∑_{m=0}^{N-1}x[m]y[(n-m)mod(N)]\] \(x[n]\)和\(y[n]\)具有相同的序列长度，两个序列长度如果不相同，使用0进行补齐。
其物理意义是将其中一个序列反转（称为反褶）后，进行\(N\)点循环时移\(m\)次，与原序列线性卷积的结果。
同样地，循环卷积也可以被矩阵化为：
\[x[n]⊗y[n]=\left[\begin{matrix} z[0] \\ z[1] \\ ...\\ z[N-2] \\ z[N-1] \end{matrix}\right]=\left[\begin{matrix} y[0] & y[N-1] & ...& y[2] & y[1]\\ y[1] & y[0] & ...& y[3] & y[2]\\ ...&...&...&...&...\\ y[N-2] & y[N-1] & ...& y[0] & y[N-1]\\ y[N-1] & y[N-2] & ...& y[1] & y[0]\\ \end{matrix}\right]\left[\begin{matrix} x[0] \\ x[1] \\ ...\\ x[N-2] \\ x[N-1] \end{matrix}\right]\] 利用矩阵化后的式子可以高效地在时域计算循环卷积。

在频域上，循环卷积对应两个序列DFT的乘积：
\[x[n]⊗y[n]↔X[k]Y[k]\]

当\(N\)大于两个序列的长度时，直接将两个序列的长度用0填充到长度\(N\)，再进行循环卷积。
当\(N\)小于两个序列的长度时，循环卷积时则会发生混叠（Alising）。长度为\(L\)的序列\(x[n]\)发生混叠的过程表示为：
\[\begin{aligned} x[0],x[1],...,&x[N],...,x[L-2],x[L-1]\\ &⇓\\ x[0]+x[N],x[1]+&x[N+1],...,x[N-1]+x[2N-1] \end{aligned}\]

循环卷积与线性卷积的关系

当循环卷积的点数大于\(2L-1\)（即线性卷积的长度）时，其结果与线性卷积（\(x[n]\*y[n]\)）完全相同。

循环卷积与周期卷积的关系

如果\(\tilde{x_1}[n]\)、\(\tilde{x_2}[n]\)分别对应是\(x_1[n]\)、\(x_2[n]\)以周期为\(N\)的延拓，有：
\[(x_1[n]⊗_Nx_2[n])R_N=\tilde{x_1}[n]\tilde{⊗}_N\tilde{x_2}[n]\] \(R_N\)表示以周期为\(N\)的延拓。
即在周期卷积对象的主值序列是循环卷积对象时，\(N\)点循环卷积是\(N\)点周期卷积的主值序列。