06. 线性调制的解调方法·抗噪性

线性调制的解调方法·抗噪性

线性调制的解调方法分为两种，其一为相干解调，适用于所有线性调制方法。其二为非相干解调（包络解波法），仅适用于调幅。

相干解调

相干解调法适用于所有的线性调制，其过程如图所示：

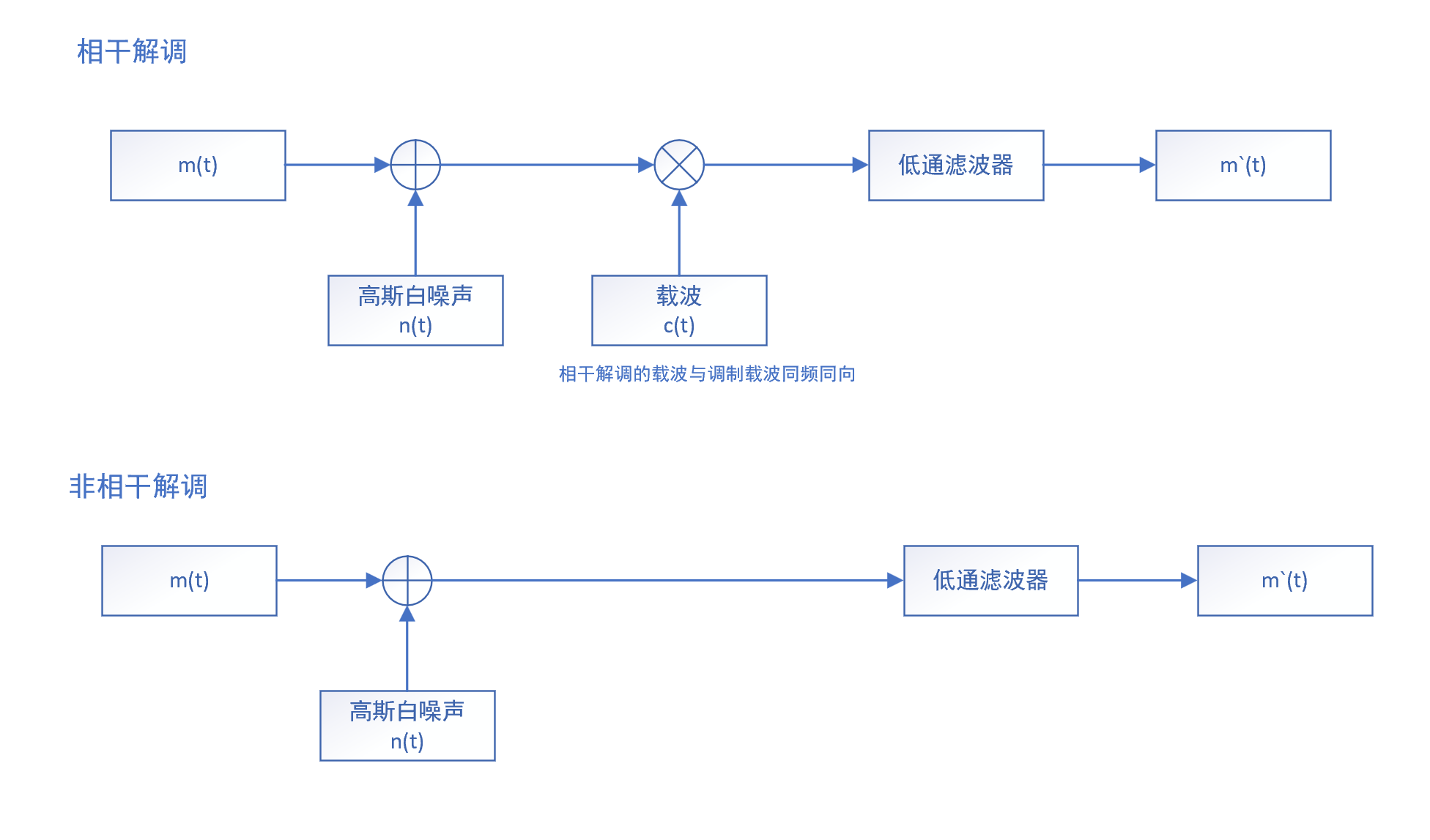
如图，当信号传入解调端后，信号与另一个同频同相的载波相乘，通过低通滤波器过滤出直流分量即可得到复原后的信号\(m_o(t)\)。

调幅、双边带调制的相干解调

对于调幅（AM）：
输入进解调部分的信号:\(S_{AM}(t)=[A_0+m(t)]cos(ω_ct+φ_0)\)。
这个信号将与一个同频同相的载波相乘：
\[\begin{aligned} ρ(t)&=[A_0+m(t)]cos(ω_ct+φ_0)cos(ω_ct+φ_0)\\ &=\frac{1}{2}[A_0+m(t)][cos(φ_0-φ_0)+cos(2ω_ct+2φ_0)] \end{aligned}\]

由于通常载波频率\(ω_c\)非常的高，因此通过低通滤波器时\(cos(2ω_ct+2φ_0)\)一项被过滤掉，只留下直流分量：
\[m_0=\frac{1}{2}[A_0+m(t)]\] > 低通滤波器只需要保证\(m(t)\)的频谱分量能够通过即可，因此理想的低通滤波器的截止频率应当为\(ω_m\)，实际上通常为\(1.5ω_m\)。

接下来信号进入减法器，减去直流\(\frac{1}{2}A_0\)后得到最终的输出：
\[m_0=\frac{1}{2}m(t)\] 对于双边带调制（DSB）其过程与上述过程基本相同，由于双边带调制后的信号不存在直流分量\(\frac{1}{2}A_0\)，因此无需通过减法器。

可以得到解调后信号的能量：
\[S_o|_{AM}=S_o|_{DSB}=\frac{\overline{m^2(t)}}{4}\]

非相干解调在\(A_0+m(t)>>n_i(t)\)时的结果和相干解调的各项值完全相同。
### 单边带调制的相干解调 进入解调部分的信号：\(S_{SSB}=\frac{1}{2}m(t)cosω_ct∓\frac{1}{2}\hat{m(t)sinω_ct}\)，与同频同相位的载波相乘：
\[ρ(t)=\frac{1}{4}[m(t)cos(φ_0-φ_0)∓\hat{m}(t)sin(φ_0-φ_0)]+\frac{1}{4}[m(t)cos(2\omega_ct+2φ_0)∓\hat{m}(t)sin(2ω_c t+2φ_0)]\] 通过低通滤波器过滤掉含有\(ω_c\)的部分：
\[m_o(t)=\frac{1}{4}[m(t)cos(φ_0-φ_0)∓\hat{m}(t)sin(φ_0-φ_0)]\] 通过时协同步器，可以得到： \[m_o(t)=\frac{1}{4}m(t)\]

可以得到解调后信号的能量：
\[S_o|_{SSB}=\frac{\overline{m^2(t)}}{16}\]

非相干解调（包络检波法）

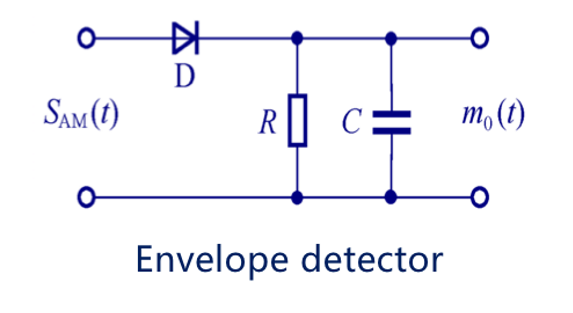
非相干解调（包络检波法）仅适用于调幅，对于\(|m(t)|_{max}≤A_0\)的调制信号，其通过如下图所示的包络线检测电路（本质上是低通滤波器的改装）后，即可消除保留波形图中幅度变化较大的部分，从而保留包络线。

相干解调过程的噪声

对于解调过程，假设输入进解调模组的加性高斯白噪声为\(n_p\)，其可以分为同相分量和正交分量两部分：\(n_p(t)=n_ccosω_ct-n_s(t)sinω_ct\)。
这两部分与载波相乘：
\[\begin{aligned} n_p(t)&=[n_ccosω_ct-n_s(t)sinω_ct]cosω_ct\\ &=\frac{1}{2}n_c(t)+\frac{1}{2}[n_c(t)cos2ω_ct--n_s(t)sin2ω_ct] \end{aligned}\] 通过低通滤波器过滤掉含有\(ω_c\)的部分：
\[n_o(t)=\frac{1}{2}n_c(t)\] 那么输出噪声的能量为： \[N_o=\frac{1}{4}N_i\] 由于DSB、AM与SSB的输入噪声能量不相同，有：
\[N_o|_{AM}=N_o|_{DSB}=\frac{n_0f_H}{2}\] \[N_o|_{SSB}=\frac{n_0f_H}{4}\] 可以得到三种调制模式在输出端的信噪比：
\[SNR_o|_{AM}=SNR_o|_{DSB}=\frac{\overline{m^2(t)}}{\frac{n_0f_H}{2}}\] \[SNR_o|_{SSB}=\frac{\overline{m^2(t)}}{\frac{n_0f_H}{4}}\]

信噪比增益

定义信噪比增益：
\[G=\frac{SNR_o}{SNR_i}\] 即解调端的信噪比与调制端的信噪比之比。
可求得三种调制模式的信噪比增益为：
\[G=\begin{cases} \frac{2\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}≤\frac{2}{3}...AM \\ 2...DSB\\ 1...SSB\\ \end{cases}\] > 在不能直接通过信噪比增益衡量调制效果的好坏，事实上，当输入信号相同时，DSB和SSB的抗噪性能理论上是相等的。

总结：线性调制的解调的性质

线性调制方法	输出信号	解调后功率	解调后噪声	输出信噪比\(SNR_o\)	信噪比增益
调幅	\(\frac{1}{2}m(t)\)	\(\frac{1}{4}\overline{m^2(t)}_{co}\) \(\overline{m^2(t)}_{noc}\)	\(\frac{n_0f_H}{2}_{co}\) \({2n_0f_H}_{noc}\)	\(\frac{\overline{m^2(t)}}{2n_0f_H}_{co}\) \(\frac{\overline{m^2(t)}}{2n_0f_H}_{noc}\)	\(\frac{2\overline{m^2(t)}}{A_0^2+\overline{m^2(t)}}≤\frac{2}{3}\)
双边带调制	\(\frac{1}{2}m(t)\)	\(\frac{1}{4}\overline{m^2(t)}\)	\(\frac{n_0f_H}{2}\)	\(\frac{\overline{m^2(t)}}{2n_0f_H}\)	\(2\)
单边带调制	\(\frac{1}{4}m(t)\)	\(\frac{1}{16}\overline{m^2(t)}\)	\(\frac{n_0f_H}{4}\)	\(\frac{\overline{m^2(t)}}{4n_0f_H}\)	\(1\)