04. 振荡器
本文最后更新于 2025年6月4日 晚上
振荡器
巴克豪森稳定性准则
反馈放大器在提升增益的同时降低了放大器的稳定性,可以利用反馈放大器在高增益下低稳定性的特点制作振荡器,使得输入的直流信号能够被振荡从而产生交流信号。
振荡器电路的框图如下:
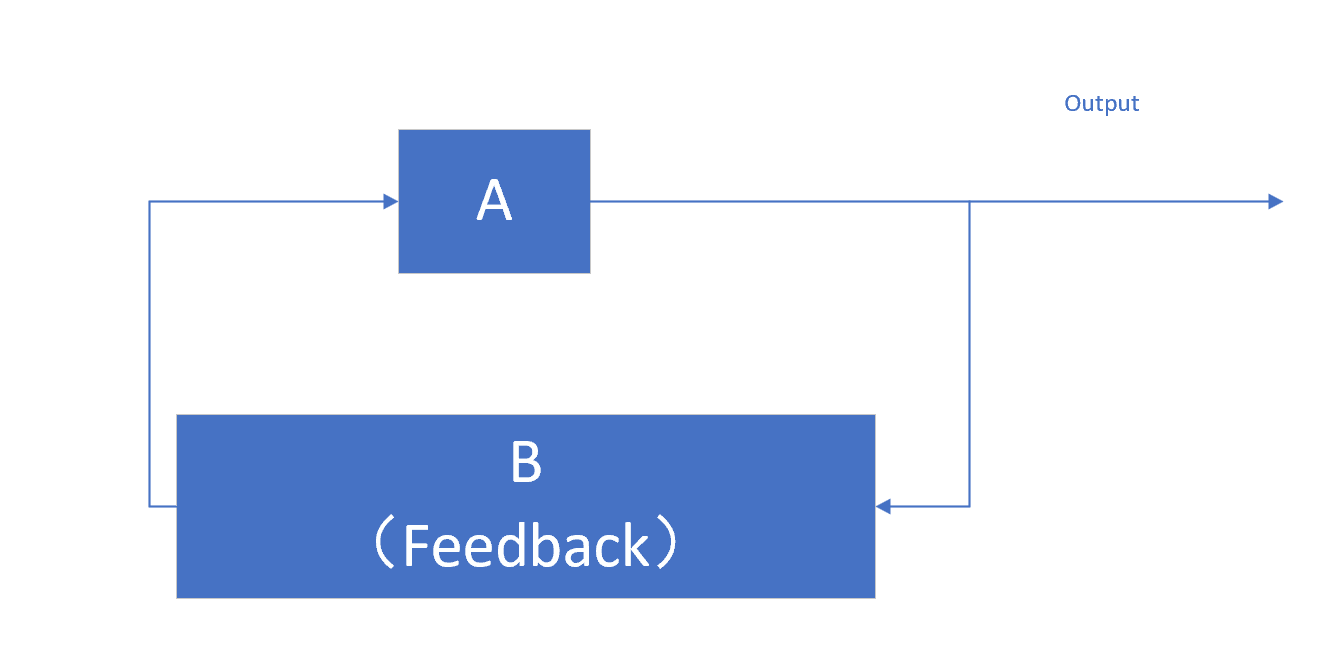
要形成稳定的振荡波形,反馈电路中不能有外源输入存在,或者说外源输入对其无影响,反馈电路中的输入只来源于噪声,根据反馈的\(G=\frac{V_{o}}{V_{in}}=\frac{A}{1-AB}\)可知,当\(|AB|=1\)时可以满足这一条件。
假设放大增益为\(A(ω_1)=|A|e^{jω_1}\),反馈增益为\(B(ω_2)=|B|e^{jω_2}\),那么整个反馈系统的前馈增益为:
\[A(ω_1)B(ω_2)=|A|e^{jω_1}|B|e^{jω_2}=|AB|e^{j(ω_1+ω_2)}\] 如果输入一个正弦噪声\(n(t)\),那么下一时刻得到的噪声为:
\[n(t+1)=|AB|e^{j(ω_1+ω_2)}n(t)\] 要想使正弦噪声的波形稳定,那么需要使得前馈增益为1.
此外,反馈信号的相位和输入信号的相位相同,否则在叠加时产生的相移会使振荡不均匀。
因此,制造稳定振荡的两个条件:
对于反馈:\(G=\frac{A_v}{1-A_vB}\),\(|AB|=1\):
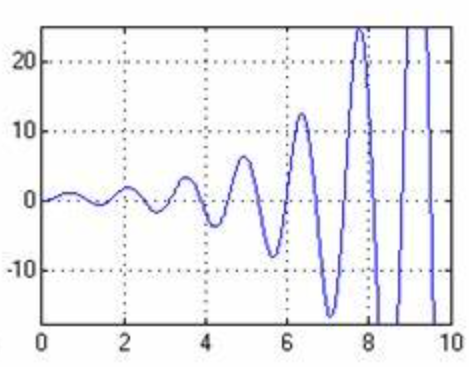
- 当\(|AB|>1\)时,每一次反馈都会加强信号,无法产生稳定的振荡波形:
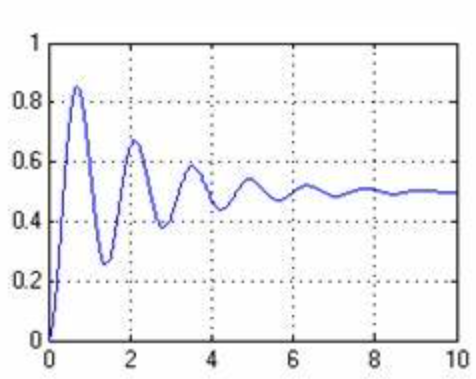
- 当\(|AB|<1\)时,每一次反馈都会削弱信号,无法产生稳定的振荡波形:
- 当\(|AB|=1\)时,每一次的反馈信号和输入信号相同,可以产生稳定的振荡波形:
- 当\(|AB|>1\)时,每一次反馈都会加强信号,无法产生稳定的振荡波形:
\(ω_1+ω_2=2nπ,n=0,1,2...\),反馈信号的相位与放大电路输入信号的相位相同。
- 对于正反馈放大器,其反馈信号的相位和输入信号的相位相同。
- 对于负反馈放大器,反馈信号的相位和输入信号的相位相差180°,因此需要人为添加相移器对相移进行复位。
这两个条件称为巴克豪森稳定性准则。满足这两个条件的反馈电路才可以产生稳定的正弦波。
文氏电桥振荡器
由于正反馈放大器可以带来振荡,负反馈放大器可以带来稳定性,文氏电桥振荡器结合了上述两种反馈放大器的优点,其电路如图所示:
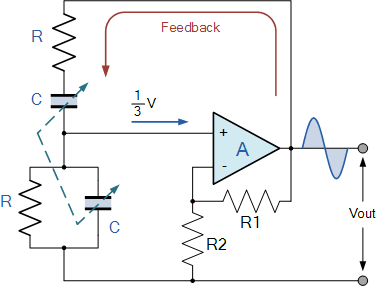
文氏电桥振荡器的 正相输入端连接的是一个由RC组成的带通滤波器电路,与正相输入端构成振荡电路,产生振荡。 其中带通滤波器的电路如下图所示:
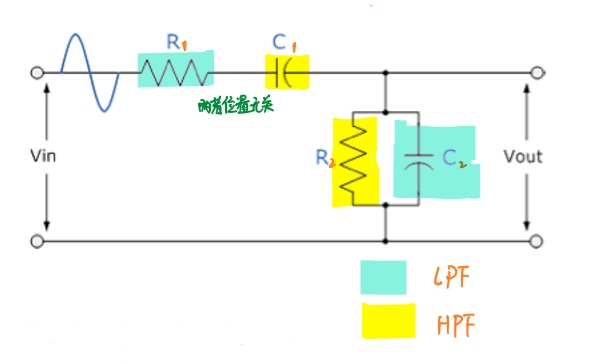
这个带通滤波器的作用是选择特定频率的信号传入正反馈放大器,从而产生振荡。
其频率响应特性曲线如下图所示:
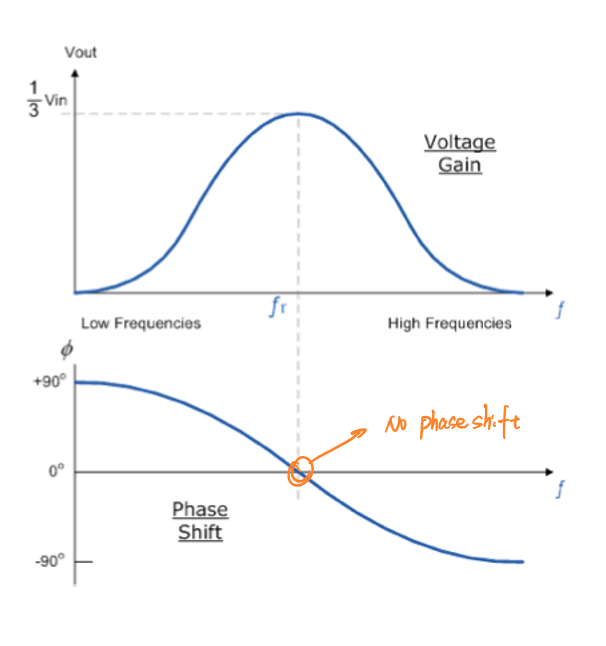
可以发现,当信号频率为:
\[f_r=\frac{1}{2πRC}\] 时,带通滤波器的相移为0,满足条件2。
文氏电桥的输出与放大器的同相输入端相连,此时放大器可以看做是一个同相放大器。
通过数学计算\(|AB|=1\)可以发现,这个结果取决于同相放大器的电压增益\(A_v\),当电压增益\(A_v=1+\frac{R_f}{R_g}≥3\)时才能满足这一条件。
这一部分的数学推导:https://blog.csdn.net/weixin_43996900/article/details/106189102
同时放大器的反相输入端可视为一个反相放大器,以负反馈确保电路输出稳定。
相移振荡器
由于负反馈放大器本身可以满足\(|AB|=1\)的条件,另一种满足相移条件的方式是将负反馈放大器连接到相移器电路上,当相移器能够实现信号相移180°时即可使电路输出稳定的正弦波。
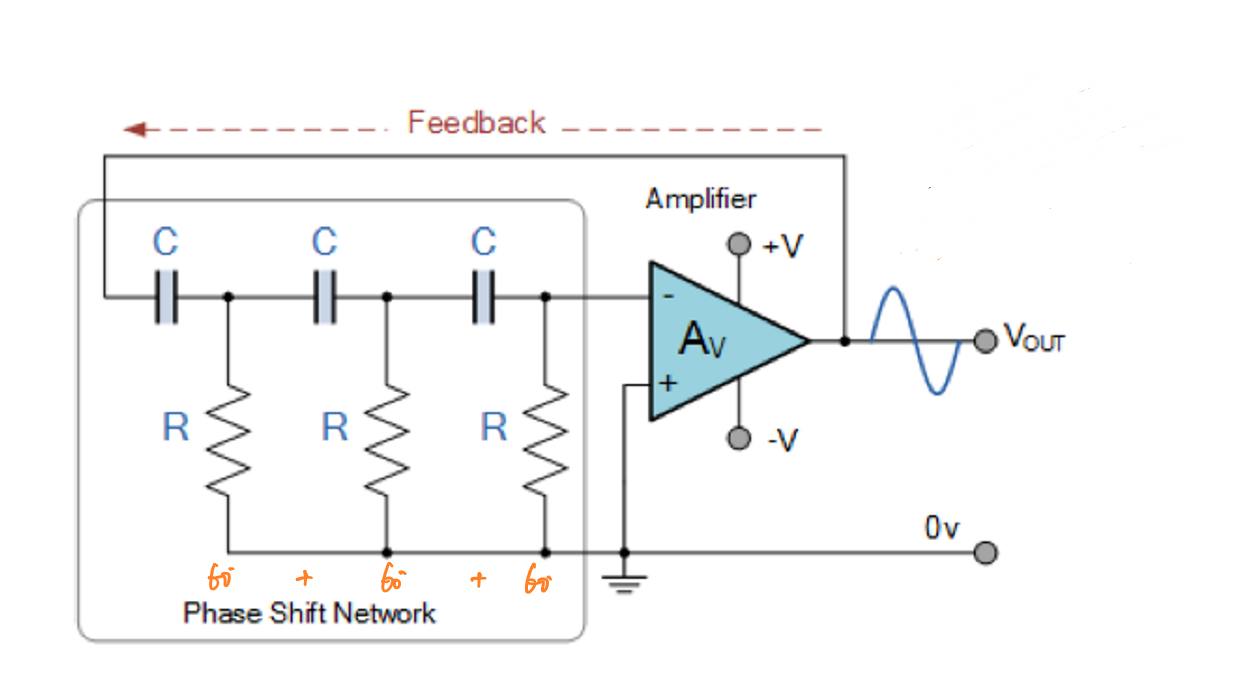
相移器
相移器通过高通滤波器的并联实现,根据高通滤波器的频率响应关系和相移公式可知,每个相移器的相移为:
\[Δφ=arctan\frac{X_c}{R}\] 通过调整电路中RC的值即可使其在输入信号频率\(f_r\)固定的情况下产生特定的相移。
当高通滤波器并联时,要使相移平均到高通滤波器,有如下公式:
\[f_r=\frac{1}{2πRC\sqrt{2N}}\] 其中\(N\)代表高通滤波器的个数,它与相移之间满足如下关系: \[Δφ=\frac{180°}{N}\] 需要注意的是,\(N\)的值越大,所需要的器件越多,同时由于每个高通滤波器在\(f_r\)处的增益都小于0,对所连接的运算放大器电压增益的要求也更高:运算放大器的电压增益需要大于所有高通滤波器在\(f_r\)的增益之和,该电路才能正常工作。通常认为\(A_v≥29\)。
同时,根据高通滤波器的相频响应图可知,二阶90°相移器的\(f_r\)无限趋近于0,不具有实用性。
松弛振荡器
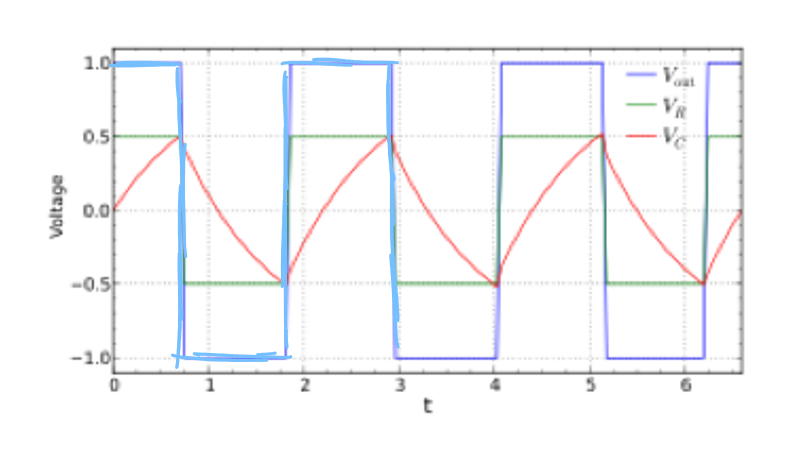
松弛振荡器电路如图所示:
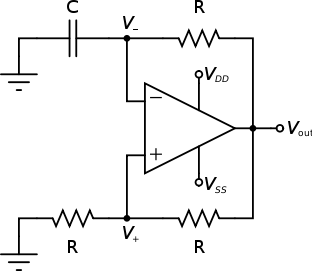
其反相输入端可以看做是一个振荡电路,通过电容的充放电可以产生三角波,而同相输入端可以看做是一个同相放大器。
当所有电阻阻值、所有电容阻值都相等时,有电路的谐振频率:
\[f_r=\frac{1}{2.2RC}\]