07. 模拟基带信号的非线性调制和解调方法

模拟基带信号的非线性调制和解调方法

载波信号：
\[C(t)=Acos(ω_ct+φ_0)\] 除了可以用载波信号的幅度携带基带信号之外，还可以用基带信号的角频率和相位携带基带信号，这两种方法都是非线性调制。
非线性调制的后信号的频谱会有额外增加的频率成分。
通常非线性调制的带宽远远大于线性调制的带宽，因此非线性调制通过牺牲其有效性增加可靠性。

调相

设载波可以表示为：\(φ(t)=K_pm(t)\) 其中\(K_p\)称为相位敏感度（Phase Sensitivity）。
\[S_{PM}=Acos(ω_ct+K_pm(t))\] 当\(m(t)=A_mcosω_mt\)时：
\[S_{PM}(t)=Acos(ω_ct+K_pA_mcosω_mt)\] 称\(m_P=K_pA_m\)为调相指数：
\[S_{PM}(t)=Acos(ω_ct+m_Pcosω_mt)\]

调频

调频将基带信号携带到相位分量的微分形式上：\(\frac{dφ(t)}{dt}=K_fm(t)\)。
其中\(K_f\)称为频率敏感度（Frequency Sensitivity）。
\[S_{FM}=Acos[ω_ct+K_f∫m(t)dt]\] 当\(m(t)=A_mcosω_mt\)时：
\[S_{FM}=Acos[ω_ct+\frac{K_fA_m}{ω_m}sinω_mt]\] 称\(m_f=\frac{K_fA_m}{ω_m}\)为调相指数：
\[S_{FM}(t)=Acos(ω_ct+m_fsinω_mt)\]

调频的非相干解调

调频可以通过非相干解调进行，输出的信号为：
\[s_o(t)=K_d[ω_c+K_fm(t)]\] 通过低通滤波器：
\[s_o(t)=K_dK_fm(t)\]

调频的相干解调（窄带信号）

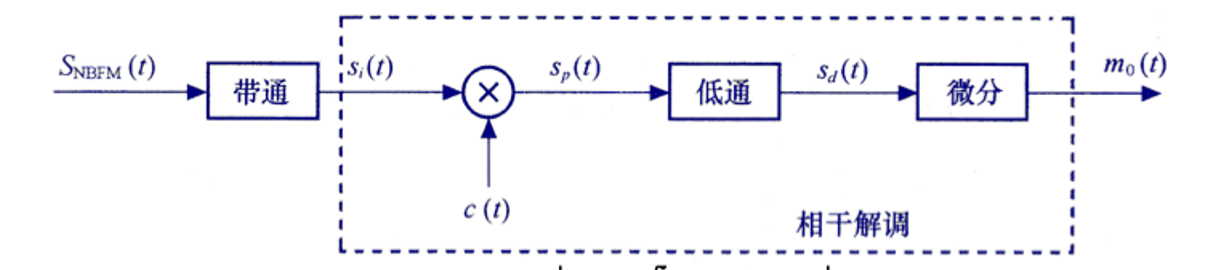
窄带信号的调频输出信号为：
\[m_o(t)=\frac{A}{2}K_fm(t)\]

宽带调频参数

宽带调频时，其带宽存在如下关系：
\[B_{FM}≈2(Δf+f_H)=2(m_f+1)f_H\] 其中\(Δf\)是最大频率分量。
调频后的能量：
\[P_{FM}=\frac{A^2}{2}\] 调频的信噪比增益：
\[G=3m_f^2(m_f+1)\]

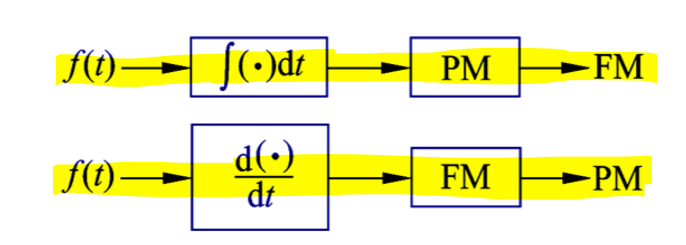
调频和调相的关系

\(f(t)\)积分后的信号通过积分器后调相的结果是其调频结果。
\(f(t)\)微分后的信号通过微分器后调频的结果是其调相结果。

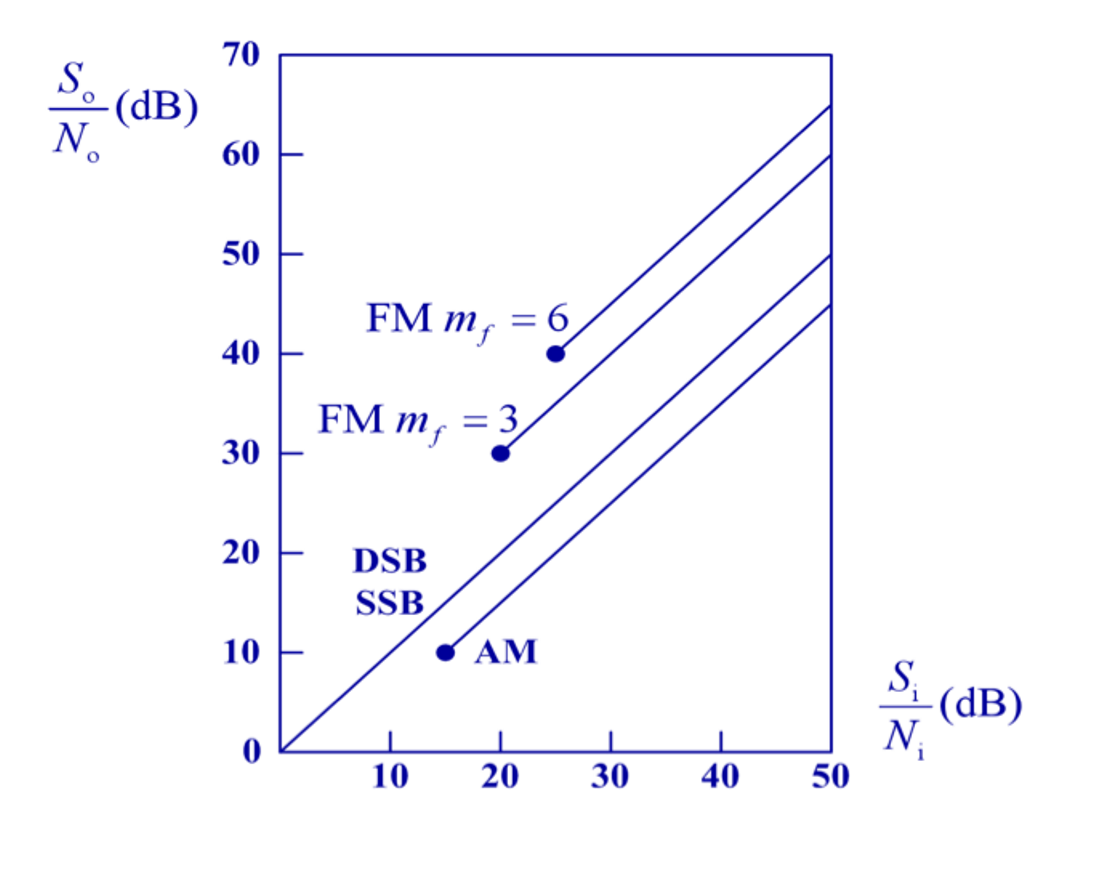
所有调制方法的信噪比增益如图所示：