08. 模拟信号的数字化/信源编码

模拟信号的数字化/信源编码

在现代通信中，更经常用到的是将模拟信号在发送端进行数字化处理后进行传输，信号在接收端进行解码还原。整个过程如下图所示：

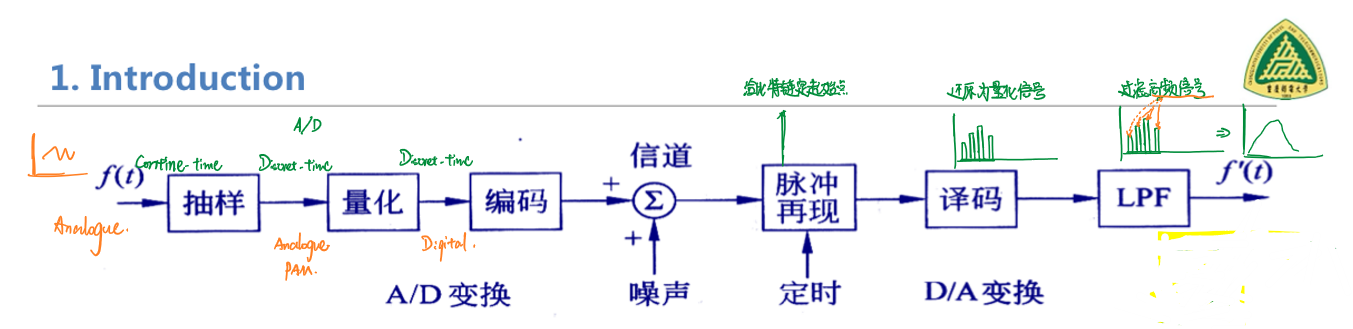
原信号经过抽样、量化后由模拟信号变成数字信号，再经过编码使得信号的幅值由无限（注意\(δ(t)\)的幅值是无限大的）变为有限描述，传输至信道，在接收端，首先通过定时规定信号的起始点和周期，再经过译码还原为量化信号（PAM，仍然是数字信号），最后通过低通滤波器过滤高频信号后在接收端还原为模拟信号\(f_o(t)\)。
> \(f_o(t)\)和\(f(t)\)实际上是不同的两个信号，原因有三：
> 1. 采样结果受到采样频率和信号变化频率的影响，不同的采样频率对同一个信号变化频率采集到的结果不同，甚至得到的采样信号可能是和原信号完全相反的波形。
> 2. 量化过程受到精度限制，极有可能获得原信号在某时间点上幅值的近似值而非准确值，这两个值之间的差距称为量化噪声。量化噪声产生后无法被消除。
> 3. 传输过程中信道的噪声和干扰。

采样

由奈奎斯特采样定理可知：采样的实质是原信号与周期冲激序列相乘:
\[m_s(t)=m(t)δ_T(t)\] 现实中很难获得一个周期冲激序列，因此改用一个周期方波序列作为抽样使用的信号。在自然采样中(Natural sampling)，采样后的每一个信号分量的幅值是随着时间变化的：

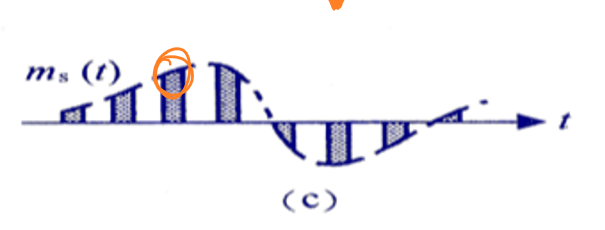
平顶抽样（Ceiling sampling）在自然采样后加入了一个保持器，可以使得信号的每一个分量的幅值被采集到后保留一段时间：

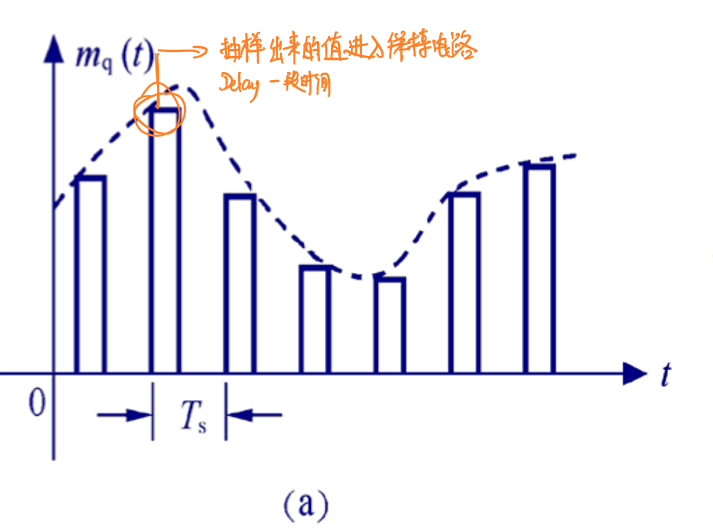
由奈奎斯特采样定理可得：
\[\begin{aligned} m_s(t)&=m(t)δ_T(t)\\ =&∑m(nT_s)δ(t-nT_s)\\ \end{aligned}\] 在频域中可得到采样后的信号频谱：
\[M_s(f)=\frac{1}{T}∑M(f-nf_s)\]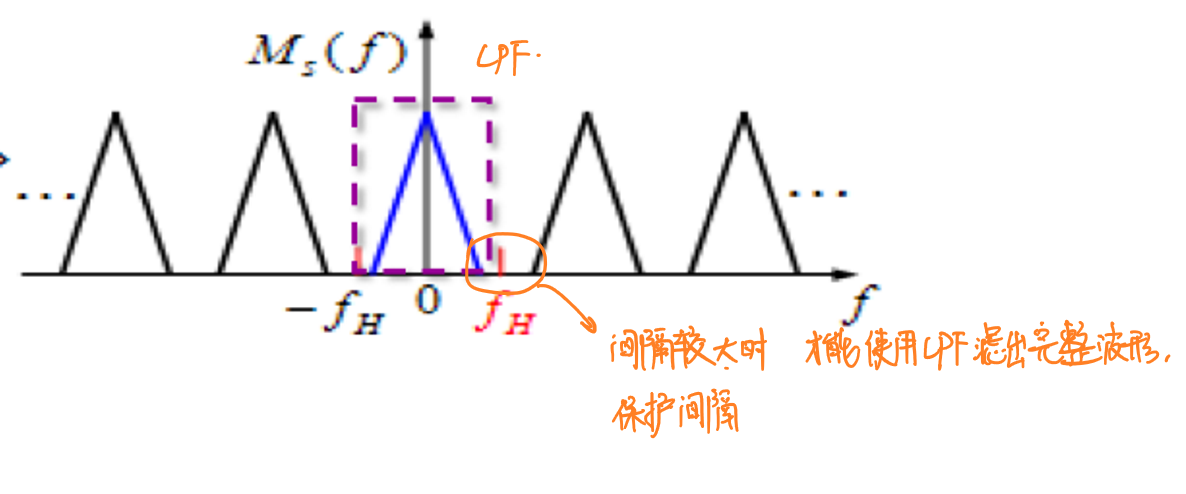

采样后频谱的每一个分量都包含原信号的完整信息，因此可以设计低通滤波器滤出一个频域周期内(\(f_s\))的信号。这种做法的前提条件是频谱分量间不能有任何的重叠，否则滤出的信号会由于重叠而产生混叠误差。（Aliasing error）

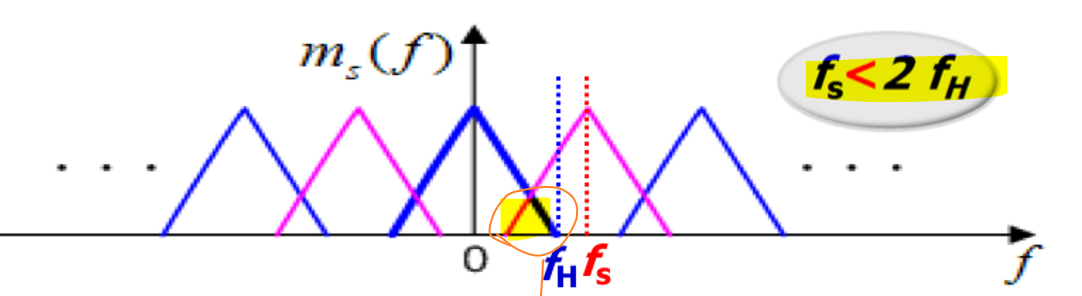
因此规定采样频率必须至少高于原信号带宽：
\[f_s≥2f_H\] 但是采样频率越高，整个频谱的带宽越大，频谱利用率越低，最好的采样频率为两者相等时：\(f_s=2f_H\)，称为奈奎斯特采样频率。

带通信号采样

这样的采样方式对低通信号（原信号频谱\(f_L=0\)）固然是可行的，对于带通信号（原信号\(f_L≠0\)），这样的采样使得频谱中出现很多无信号部分，称为频谱空洞，导致频谱利用效率降低。因此需要在上述方法上进行改进。

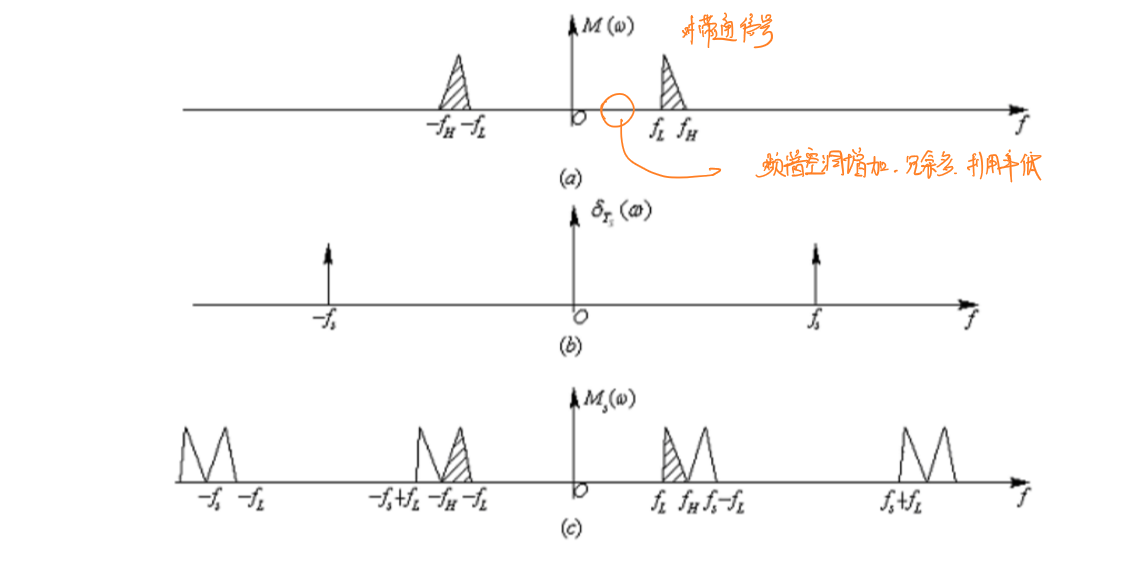
对于带通信号，其采样频率\(f_s\)应当满足如下条件：
\[f_s≥2B(1+\frac{M}{N})\] 其中\(M\)为\(|\frac{f_H}{B}|\)的小数部分，\(N\)为\(|\frac{f_H}{B}|\)的整数部分。
满足\(f_s=2B(1+\frac{M}{N})\)的采样结果不会出现频谱空洞。
对于上式，当\(f_L\)非常大时，\(f_s≈2B\)。

量化

均匀量化

量化过程简述如下：将信号的幅值划分成若干个区间，某时刻原信号幅值落在该区间时，量化信号在此时刻的幅值为这个区间的中值。

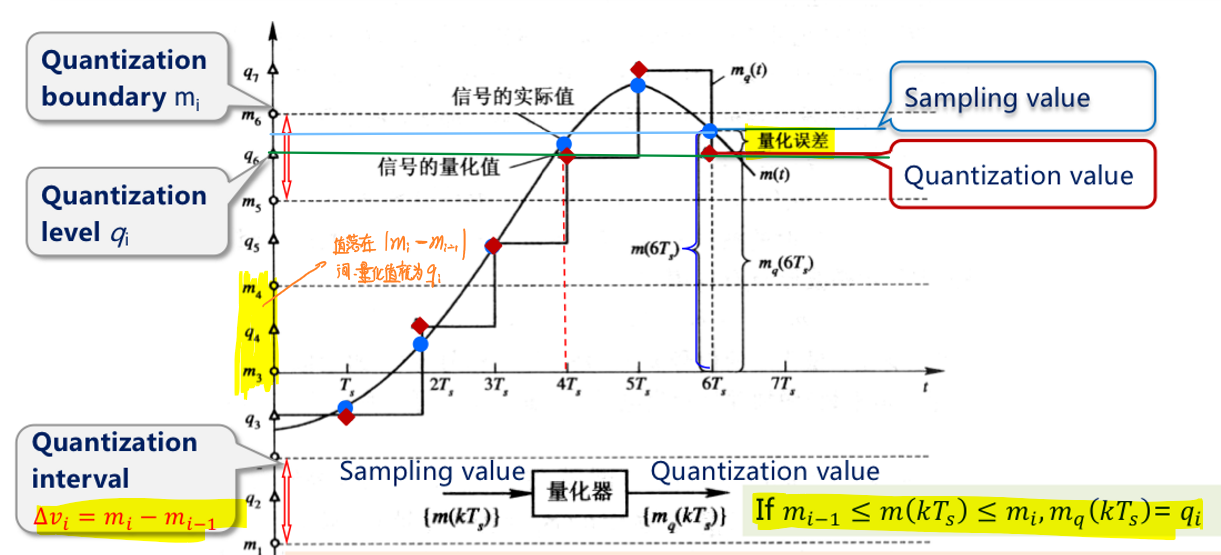
该过程可以用数学表示为：
\[m_q(kT_S)=q_i,\text{if }m_{i-1}≤m(kT_s)≤m_i\] 这个过程中的每个区间称为量化间隔，在均匀量化中，这个间隔是均等的：\(Δ=\frac{V_m}{N}\)，\(N\)为用于描述信号的比特数，与量化精度相关。每个区间的上界是下一个区间的下界，每个界限以\(m_i\)表示。当原信号落入某区间时，用于描述/替代原信号幅值的值称为量化电平\(q_i\)，量化电平通常是该区间的中值，以减小总体的量化误差：
\[q_i=\frac{m_i+m_{i-1}}{2}\]

均匀量化的信噪比

输入信号的平均功率：
\[S=E[(m_k)^2]=∫x^2f(x)dx\] \(m_k\)表示采样值，\(m_q\)表示量化值。
量化值与实际值之间的误差称为量化误差/量化噪声，量化噪声的功率在数学上表示为：
\[N_q=E[(m_k-m_q)^2]=∫_a^b(x-m_q)^2f(x)dx\] \(f(x)\)是原信号的概率密度函数，原信号需要符合均匀分布才能使用均匀量化。
带入\(m_i=a+iΔ\)，\(q_i=a+iΔ-i\frac{Δ}{2}\)后化简计算，可以发现量化噪声的功率只与量化间隔有关。
定义量化信噪比为输入的采样信号功率与量化噪声的功率之比：
\[\frac{S}{N_q}=\frac{E[(m_k)^2]}{E[(m_k-m_q)^2]}\]

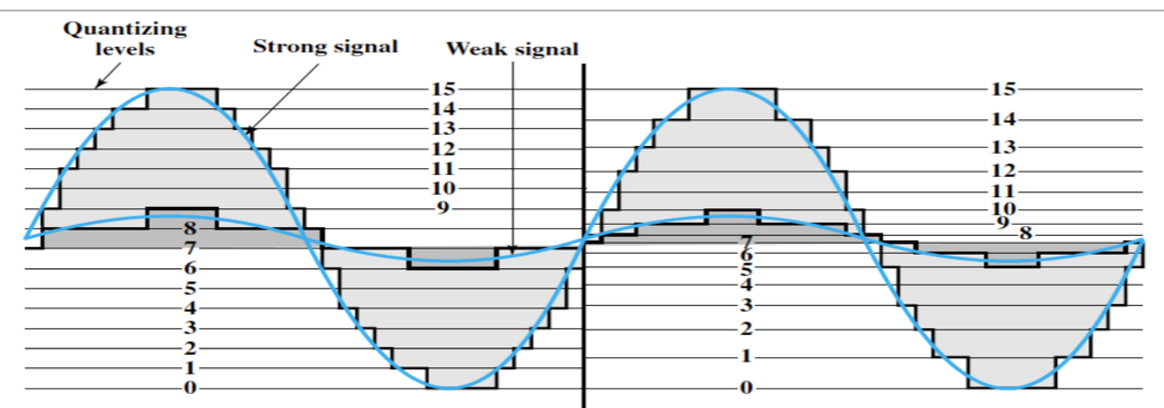
从上述结论可以发现，量化噪声与输入信号的功率大小无关，因此小的输入信号功率会导致非常小的量化信噪比。

非均匀量化

解决“小的输入信号功率会导致量化信噪比小”这一问题的基本思路是使用一个函数对信号的幅值进行重映射，使其能够扩大小功率时的幅值，缩小大功率时的幅值。这个函数称为压缩律。输入信号经过压缩器使用压扩器增大小功率信号的幅值后，再使用均匀量化就能减小量化信噪比。在接收处，通过压缩率的反函数可以对压缩信号进行还原。

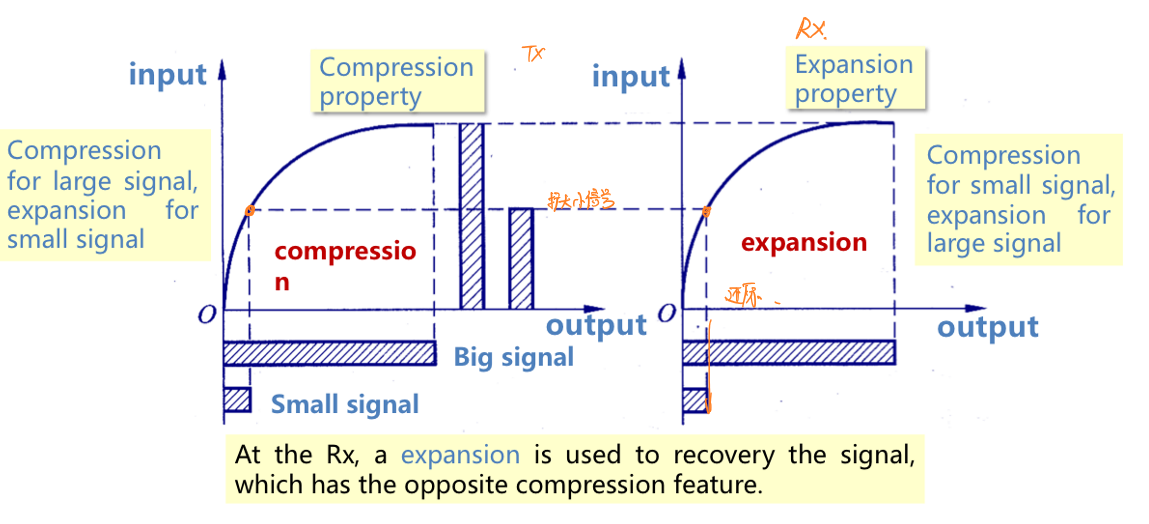
国际电信联盟（ITU）所采用的两种压缩律分别为A压缩律和μ压缩律，A压缩律在中国和欧盟国家使用，μ压缩律在美国、日本、韩国使用，国际通信时使用A压缩律作为标准。本章只介绍A压缩律。
A压缩律可以用如下公式表示：
\[y=\begin{cases} \frac{Ax}{1+lnA},0≤x≤\frac{1}{A}\\ \frac{1+ln(Ax)}{1+lnA},\frac{1}{A}≤x≤1 \end{cases}\] 其中\(x\),\(y\)分别表示最大值归一化后压扩器的输入和输出信号。

A压缩律的数字化

在数字系统中，压缩律通过折线对模拟压缩律进行近似，ITU规定数字化的A压缩律以13折折线近似，μ压缩律以15折折线近似。对A压缩律，具体的表示方法如下：

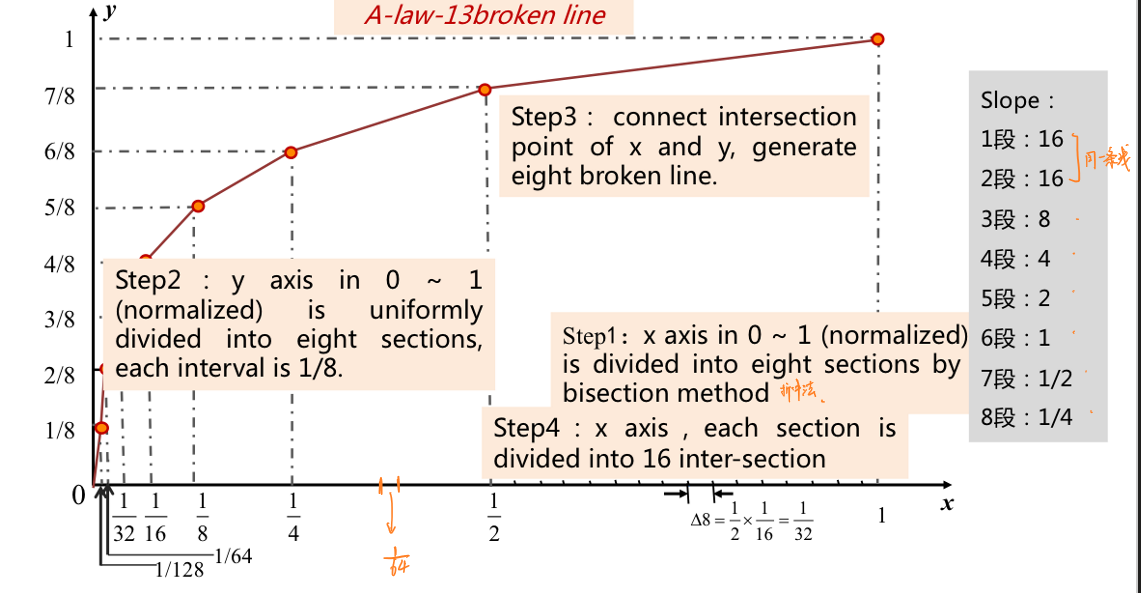
1. 将最大值归一化后的\(x\)轴采用折中法反复折中，划分为8段落（\(0-\frac{1}{128}\)到\(\frac{1}{2}-1\)），称为量化段。对于每一个段落，分为16个小区间，称为量化级。最小的区间长度出现在\(0-\frac{1}{128}\)段，定义\(Δ=\frac{1}{128×16}=\frac{1}{2048}\)。每一量化段的量化间隔如下表所示：
   

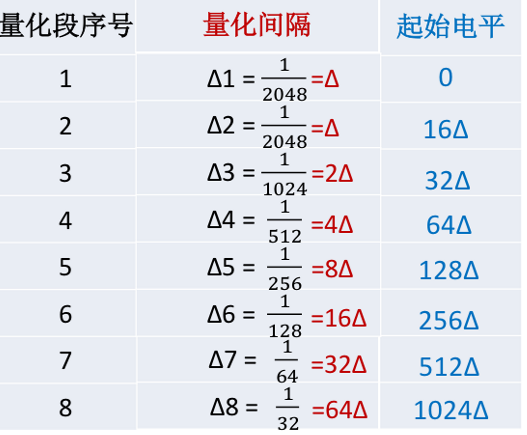
   需要注意，声音信号的幅值分布在I象限和III象限，因此量化折线还需要镜像对称到第III象限。由于-2，-1，1，2四个量化段的斜率相等，是同一条线，因此一共使用了13条折线来描述A压缩律（I象限、III象限）。
   

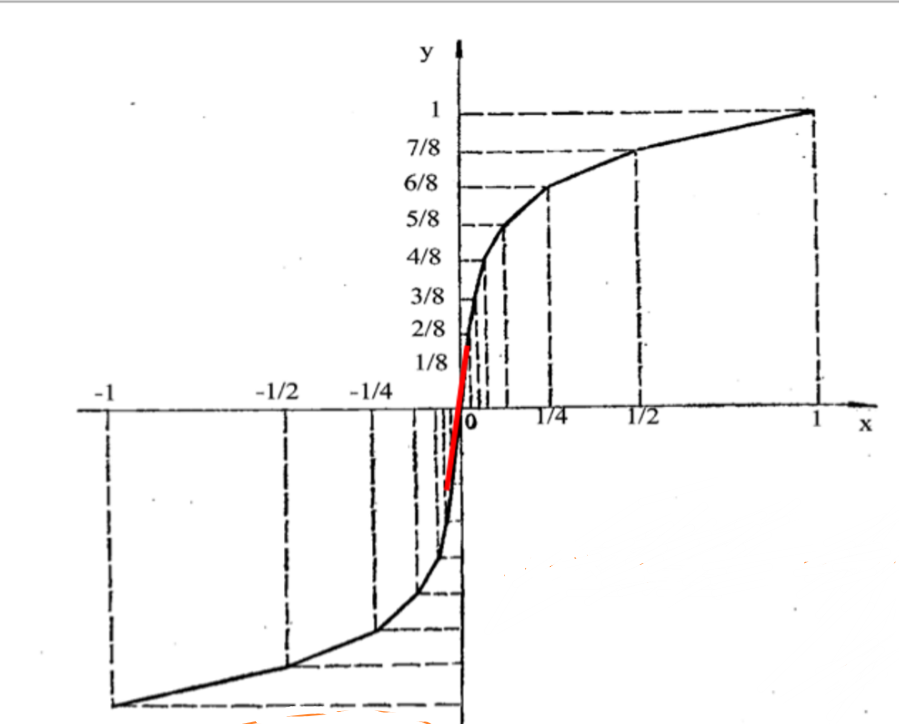
   那么\(x\)轴一共有256个量化级，可以用8bit进行表示：
   \[M=2×8×16=2^8\]

2. \(y\)轴平分为8段，每一段间隔相等。
   

3. 连线。

编码

通信系统中常用的编码有三种：
1. 自然二进制编码（NBC） 2. 格雷码 3. 折叠码（FBC）

折叠码

本节着重介绍折叠码，折叠码化需要选取折叠的位置，取折叠码第一位表示极性，即是折叠位置以上（正，1）还是折叠位置以下（负，0），然后出去极性，将值到折叠位置的距离二进制化，得到该值对应的折叠码。

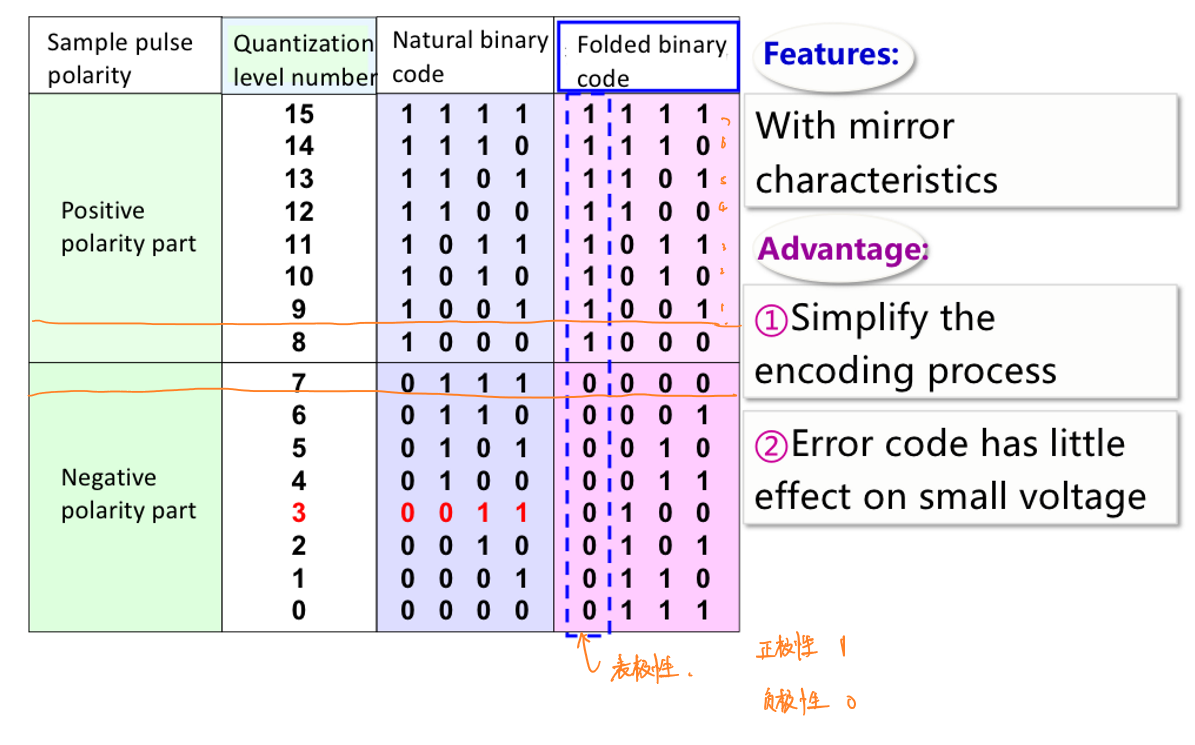
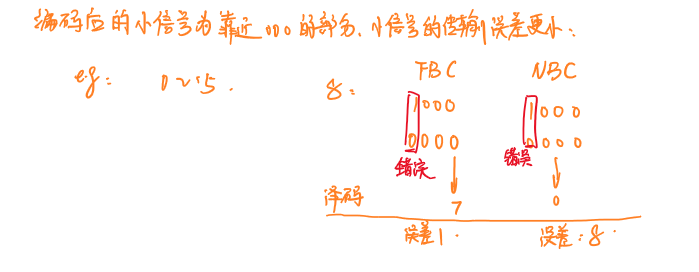
折叠码的优势在于，对相同的点平/值，折叠码表示所用的比特数要少于自然二进制编码。此外，折叠码对小信号（0附近的信号）比较友好，当表示极性的比特位发生错误时，对应的电平误差只有1。

脉冲编码调制（PCM）

脉冲编码调制是基于A压缩律的非均匀调制的一种编码方法，是一种折叠码。但是由于声音格式有负幅值，因此其折线位于0处。PCM采用了如下格式进行编码：

	极性码	段落码	段内码
	\(C_1\)	\(C_2C_3C_4\)	\(C_5C_6C_7C_8\)
意义	极性	对应8个段落	对应每一个段落中的16个量化级

PCM编码与数字化的13折A压缩律对应如下：

段落编号	电平区间	段落码	量化间隔Δ
1	0-16	000	\(1=2^0\)
2	16-32	001	\(1=2^0\)
3	32-64	010	\(2=2^1\)
4	64-128	011	\(4=2^2\)
5	128-256	100	\(8=2^3\)
6	256-512	101	\(16=2^4\)
7	512-1024	110	\(32=2^5\)
8	1024-2048	111	\(64=2^6\)

脉冲调制编码过程

量化后的电平值转化为脉冲调制编码的步骤为：
1. 判断电平的正负，如果是正：\(C_1=1\)，如果为负，\(C_1=0\)。 > 注意“1正0负”

2. 根据电平值和电平区间，判断电平落在了哪一个段落，决定段落码\(C_2C_3C_4\)。
   
3. 将电平值减去段落的起始值，与量化间隔相除，结果转化为8421码即为\(C_5C_6C_7C_8\)。

与量化间隔相除结果的余数部分无法通过编码表示，称为编码噪声\(N_e\)。
由于这样的转换方式比较低效，实际上的通信系统通常采用逐位进行比较的逐次比较法，过程如下图所示：

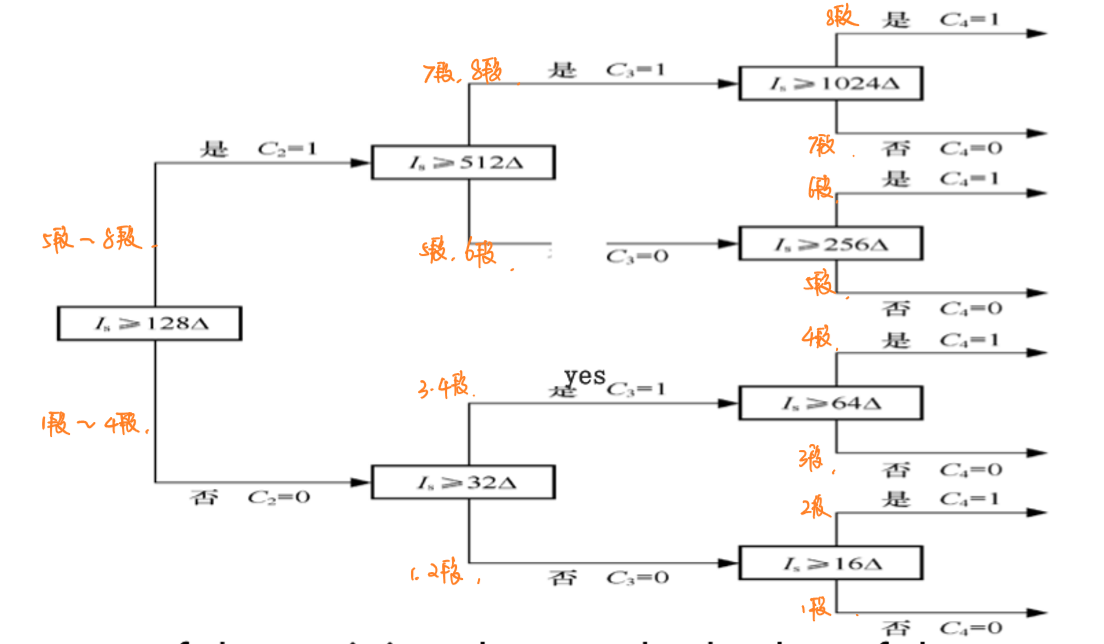
脉冲调制的解码

PCM编码在解码端首先会变成11位的自然二进制编码。
#### PCM与11-NBC的关系 PCM基于非均匀脉冲，是一种非线性编码。由于之后的通信电路中含有仅支持线性输入的逻辑电路，因此还需要将7bit的PCM转化为11bit的自然二进制编码（NBC），两者之间满足：
\[I_{PCM}=I_{11-NBC}\] 即两者编码转化为10进制的结果是相同的。
因此PCM编码转为10进制后再转为自然二进制即可得到NBC。

PCM与12-NBC的关系

由于PCM编码只考虑到了每个量化区间内的起始值\(m_{i-1}\)而并非量化电平\(p_i\)，在解码过程中需要补充每个量化段的半个量化区间\(\frac{Δ_i}{2}\)，由于最小的\(\frac{Δ_1}{2}=0.5\)，因此需要额外补充一个bit来弥补增加的精度，生成12位NBC码。
\[I_{12-NBC}=I_{PCM}+\frac{Δ_i}{2}\] 因此，脉冲编码调制的量化噪声\(N_q\)为编码噪声减去\(\frac{Δ_i}{2}\): \[QN=EN-\frac{Δ_i}{2}\]

PCM的抗噪性分析

传输速率

PCM的传输速率为：
\[R_B=f_s×log_2M\] 其中\(f_s\)为采样频率，\(M\)为比特数，A律13折PCM中\(M=256\)。

信噪比

解码器端解码后的信号可以表示为：
\[\hat{m}(t)=m_0(t)+n_q(t)+n_e(t)\] \(n_q(t)\)为量化噪声，\(n_e(t)\)为传输过程中的高斯白噪声。
因此整个过程的信噪比表示为：
\[\frac{S_o}{N_o}_{PCM}=\frac{\overline{m^2(t)}}{N_q+N_e}\] 通过计算可以发现，当\(m(t)\)服从均匀分布时，量化信噪比表示为：
\[\frac{S}{N_q}=M^2\]

时分复用

时分复用（TDM）可以达到在一个小时间段内同时传输多条信号的目的。

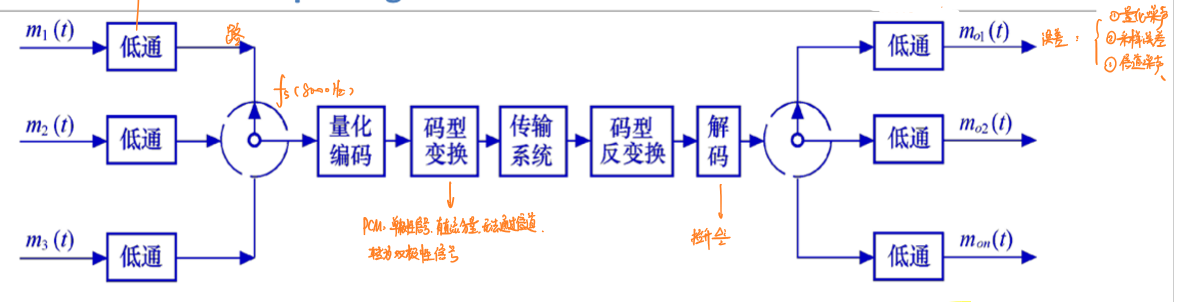
如上图所示，多路信号作为输入，每一路的输入信号都要通过一个低通滤波器以保证信号的最高频小于\(f_H\)(对于声音信号是3400Hz)，保证采样时可以抽取到所有的信息。此后，多路信号汇合，通过一个抽样转盘，该抽样转盘会在一个周期内均匀地抽取每一路信号的一部分，对于声音信号，抽样转盘的采样频率为\(f_s=8000Hz\)。
在解码端也存在一个与发送端频率完全相同的抽样转盘，该转盘在一个周期内会将经过时分复用后的信号还原分配给每一路信号。

对于每一路信号，抽样转盘能够提取这路信号的时间段称为一个路时隙\(T_a\)（Time slot），每一路信号的一个路时隙组成一帧（Frame），即抽样转盘的采样周期\(T_s\)，二者存在如下关系：
\[T_a=\frac{T_s}{n}\] \(n\)表示信号的路数。
对于PCM信号，每一路信号的一个路时隙信息量为8bit，即一个路时隙的字长\(l=8bit\)，因此对于TDM-PCM信息传输速率可以表示为：
\[R_B=R_b=nlf_s\] \(f_s\)为转盘的抽样频率。

占空比

对每一帧而言，其中电平不为0的时间段（即信息传输的时间）称为符号持续时间\(τ\)（Symbol duration），定义占空比（Duty Cycle）表示符号持续时间和一个周期时间之比：
\[Duty.Cycle=\frac{τ}{T_s}×100\%\] 当\(τ=T_s\)时，表示一个周期内所有时间都在发送符号，称为归零码（RZ Code），\(τ≠T_s\)时，称为不归零码（NRZ Code）。

30/32 PCM 基群结构*

30/32 PCM 基群结构是我国普遍使用的TDM-PCM方式，一帧有32个路时隙，其中有2个路时隙用于传输同步信号，剩余的30个路时隙用于传输信息。
其中TS0用于传输同步码、监视码、对端告警码组（简称对告码）；TS16用于传输信令码；TS1—TS15传前15个话路的话音数字码，TS17—TS31传输后15个话路的话音数字码。
此外还有16个复帧（Multi-frame）用于特殊用途（如定位信号，CRC校验码，信令传输等等）。

信令是用来表示通话状态的一系列信息，如：摘机、挂机信号、拨号、忙音等。