07. 晶体管的直流偏置状态

晶体管的直流偏置状态

晶体管的偏置类型

BJT晶体管只有在直流工作状态下，才能作为放大器或者开关正常工作。在实际设计中，有两种方式来控制静态工作点（\(I_C\)和\(V_{CE}\)）的值：
- 基极偏置 在基极偏置下，保持\(I_B\)始终不变来设置\(I_C\)和\(V_{CE}\)的值。
基极偏置通常用于晶体管作为开关时。
- 发射极偏置 在发射极偏置下，保持\(I_E\)始终不变来设置\(I_C\)和\(V_{CE}\)的值。
发射极偏置通常用于晶体管作为放大器时。

基极偏置

基极偏置的电路图如图所示：

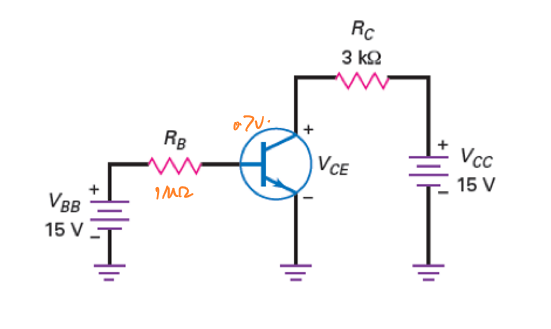
基极偏置下，发射极接地，基极接入一个直流电压\(V_{BB}\)。当\(V_{BB}\)和\(R_B\)固定时（这两个值已知），\(I_B\)固定。 通过对基极环路和集电极环路应用基尔霍夫电流/电压定律计算出\(I_C\)和\(V_{CE}\)。
\[\begin{aligned} I_B&=\frac{V_{BB}-V_{BE}}{R_B}\\ I_C&=βI_B\\ V_{CE}&=V_{CC}-I_CR_C\\ \end{aligned}\] 可以发现这个计算过程中要用到电流增益\(β\)，因此静态工作点的选取和\(β\)有关。
由于静态工作点对\(β\)极为敏感，因此静态工作点很容易出现在饱和和截止区域，因此基极偏置通常用于晶体管作为开关时。
> 饱和状态下可以通过计算\(I_{CSat}\)反求\(I_B\)。

反馈偏置*

由于电流增益\(β\)的大小与温度、器件本身等诸多因素有关，在电路设计时应当尽量避免\(β\)对电路的输出产生影响，导致不稳定的结果。反馈偏置就是一类利用负反馈对\(β\)变化而导致的静态工作点变化进行抑制的电路。
### 发射极反馈偏置 由于基极偏置的静态工作点对\(β\)极为敏感，考虑使用负反馈让\(I_C\)不会产生过多变化。发射极反馈偏置就是采用这样一种思路的电路，其结构如下图所示：

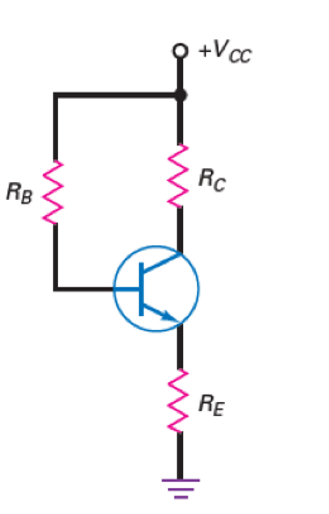
在这个电路中：
如果\(I_C\)增大，由\(I_C≈I_E,V_E=I_ER_E\)可知\(V_E\)会增大；
由\(V_{BE}=V_{B}-V_E=0.7V\)可知\(V_B\)增大；
由\(V_B=V_{BB}-I_BR_B\)可知\(I_B\)减小；
由\(I_C=βI_B\)可知\(I_C\)最终会减小。
反之亦然。
但是相比于静态工作点不随\(β\)发生任何变化的发射极偏置而言，\(β\)仍然对发射极反馈偏置存在影响：虽然存在负反馈限制\(I_C\)的变化，但是在实际过程中\(I_C\)的变化仍可能不满足设计需求，因此发射极反馈偏置电路不常用。

集电极反馈偏置

集电极反馈是另一种尝试负反馈来抑制\(I_C\)发生变化的电路，其结构如图所示：

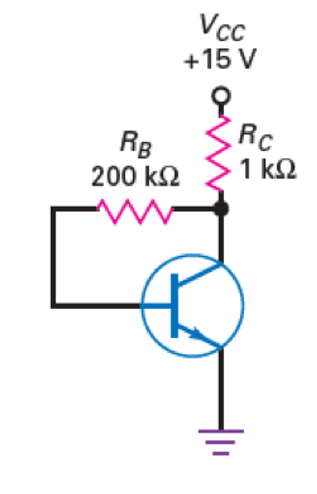
在这个电路中：
如果\(I_C\)增大，由\(V_C=V_{CC}-I_CR_C\)可知\(V_C\)减小；
由\(V_B=V_{BE}=V_{C}-I_BR_B=0.7V\)可知\(I_B\)减小；
由\(I_C=βI_B\)可知\(I_C\)最终会减小。
反之亦然。
在实际应用中，由于比发射极反馈偏置电路图更简单，集电极反馈偏置的负反馈更容易抑制\(I_C\)的变化，但是也对\(β\)很敏感。

集电极-发射极反馈偏置*

集电极-发射极反馈偏置试图综合上述两种反馈偏置的负反馈效果，来达到更好抑制效果的目的。但是事实上，集电极-发射极反馈偏置虽然优于前两者的反馈抑制效果，但是很难大规模生产，因此不常应用，其电路图如下图所示。

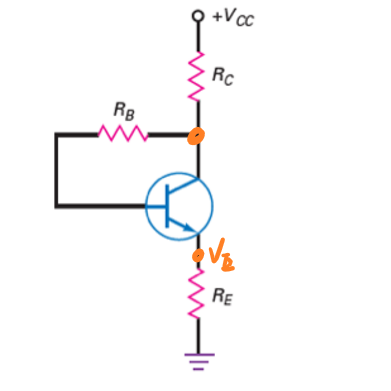
发射极偏置

发射极偏置的电路如图所示：

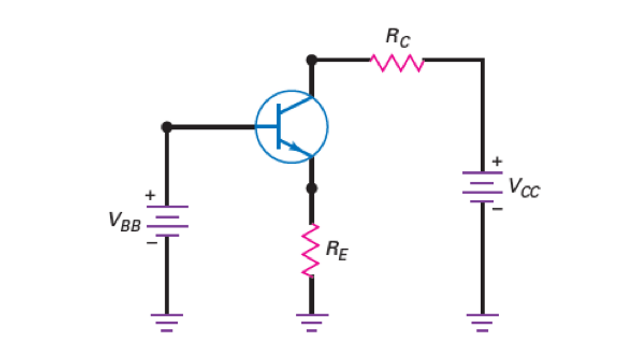
发射极偏置下，发射极接入一个电阻\(R_E\)，在\(V_{BB}\)和\(V_{BE}\)的作用下，发射极产生一个发射极电流\(I_E\)。当给定\(R_E\)和\(V_{BB}\)时，\(I_E\)固定不发生变化。 通过对基极环路和集电极环路应用基尔霍夫电流/电压定律计算出\(I_C\)和\(V_{CE}\)。
在这种情况下：
\[\begin{aligned} I_E&=\frac{V_{BB}-V_{BE}}{R_E}\\ I_E&≈I_C\\ V_{CE}&=V_C-V_E\\ &=V_{CC}-I_CR_C-I_ER_E \end{aligned}\] 可以发现，此处计算\(I_C\)时不会用到\(β\)，即静态工作点的选取与\(β\)无关。这种情况下的静态工作点较为稳定，处于放大区域内，因此发射极偏置常用于晶体管作为放大器时。

发射极偏置的变形

分压偏置

分压偏置（Voltage Divider Bias，VDB）的电路图如图所示：

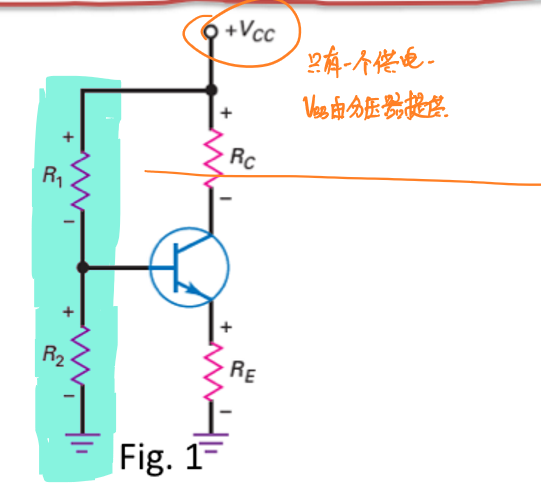
分压偏置其实是发射极偏置的改装：与发射极偏置的唯一不同点在于基极供电\(V_{BB}\)直接由\(V_{CC}\)和分压器提供：
\[V_{BB}=\frac{R_2}{R_1+R_2}V_{CC}\] 其余计算与分压偏置相同。

双电源发射极偏置

双电源发射极偏置（Two supply Emitter Bias，TSEB）结构如图所示：

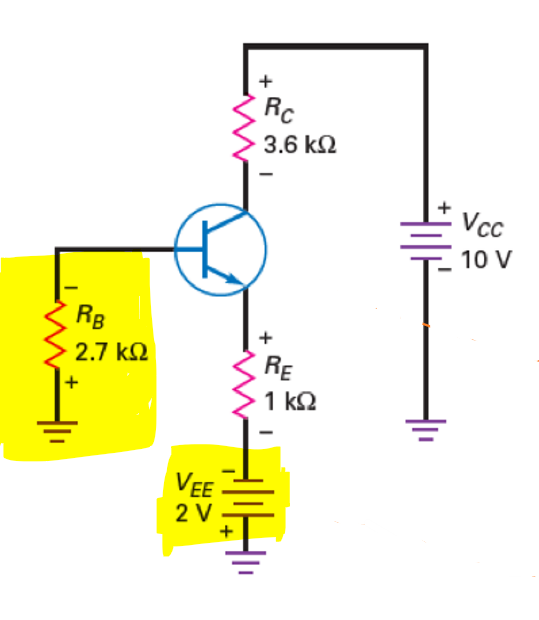
在这种情况下，发射极有两个直流电压源\(V_{BE}\)和\(V_{EE}\)。由于基极连接电阻后直接接地，\(I_B\)非常小，可以认为\(V_{B}=0\)。
因此对于发射极：
\[V_E=0-V_{BE}=-0.7V\] \[I_E=\frac{V_E-V_{EE}}{R_E}\] 其余计算同发射极偏置。

偏置类型	恒定量	电路特征	静态工作点与\(β\)独立？
基极偏置	\(I_B\)	基极端有电阻\(R_B\)	否
发射极偏置	\(I_E\)	发射极端有有电阻\(R_E\)	是