09. 数字基带传输系统中信号的码型、波形和频谱

数字基带传输系统中信号的码型、波形和频谱

数字基带传输系统简述

数字基带传输系统的模型如图所示：

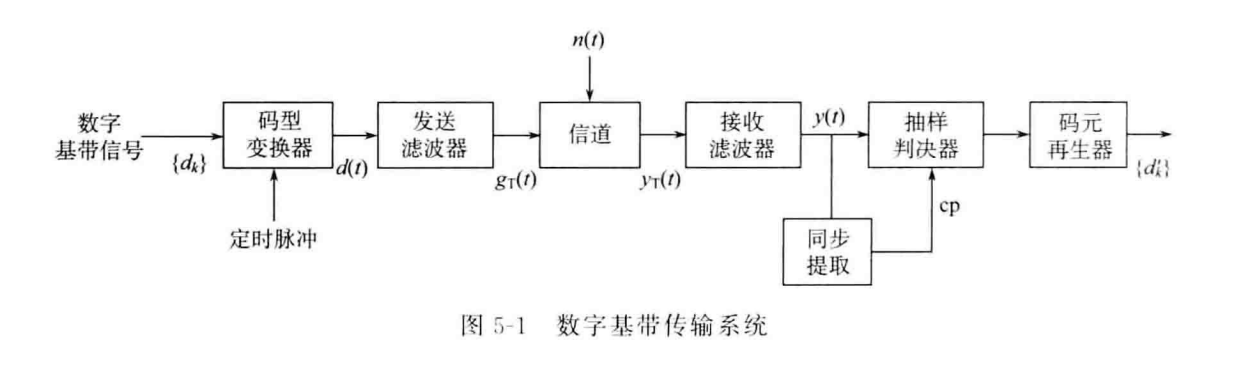
经过脉冲编码调制的PCM编码成为数字信号(a)，通过脉冲形成器由单极性码变成双极性码(b)，并提供定时脉冲(f)。生成的双极性码信号通过发送端的低通滤波器过滤掉高频分量后，成为升余弦波形(c)。

由0/1组成的编码称为单极性码。单极性码含有直流分量，无法通过由逻辑门电路构成的判决器。双极性码含有负电平（逻辑中以-1表示）。

定时脉冲是周期为\(T_s\)的冲激序列，目的是为了让接收端知道每个字符（0/1/-1）的持续时间和出现时间间隔。

数字基带传输系统的信道常采用线缆、明线。在信道中存在加性噪声，使信号发生失真等现象(d)。
发送的模拟信号在接收端通过低通滤波器过滤掉信道中的加性噪声(e)，在同步提取模块中提取出信号的定时脉冲(f)，接收信号和这个定时脉冲被送入抽样判决器：抽样判决器会在每一个定时脉冲时判断接收信号的电平大小对应数字信号的1还是0，抽样判决器生成信号如(g)所示。最终，接收信号被复原为数字信号(h)。
数字传输系统中各阶段的波形如图所示：

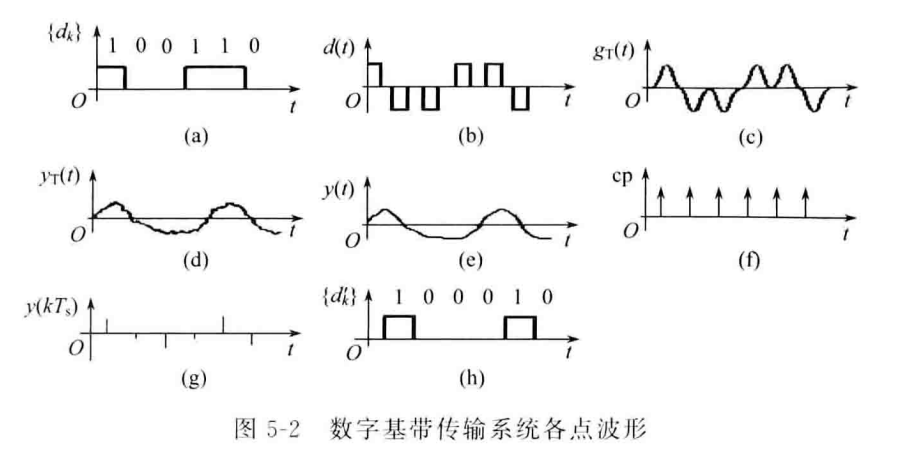
码间串扰

通过上图可以看出，原来的PCM信号在传输过程中产生了失真，使得原有的两个字符信号发生重叠而无法被判决器识别，最终导致误码。这样的两个字符重叠而产生的干扰称为码间串扰（Inter Symbol Interferance, ISI）。如何减少传输过程中的码间串扰是数字通信中的一个重点问题。

信道编码的码型设计

码型设计标准

原始信息编码为方便基带数字信号传输系统传输的编码方式（称为码型）。通常认为，对码型的要求包含如下几点：
1. 在编码阶段不能包含直流分量，且低频分量少。
2. 码型要便于提取出定时脉冲。
3. 具备纠错、检错能力。
4. 高频分量尽量少，以减小码间串扰。
5. 传输和变换设备简单，便于实现。

码型选择

根据有无极性和是否归零可以将可能的编码大致分成四类：单极性归零码、单极性不归零码、双极性归零码、双极性不归零码。其频域内频谱图如下图所示：

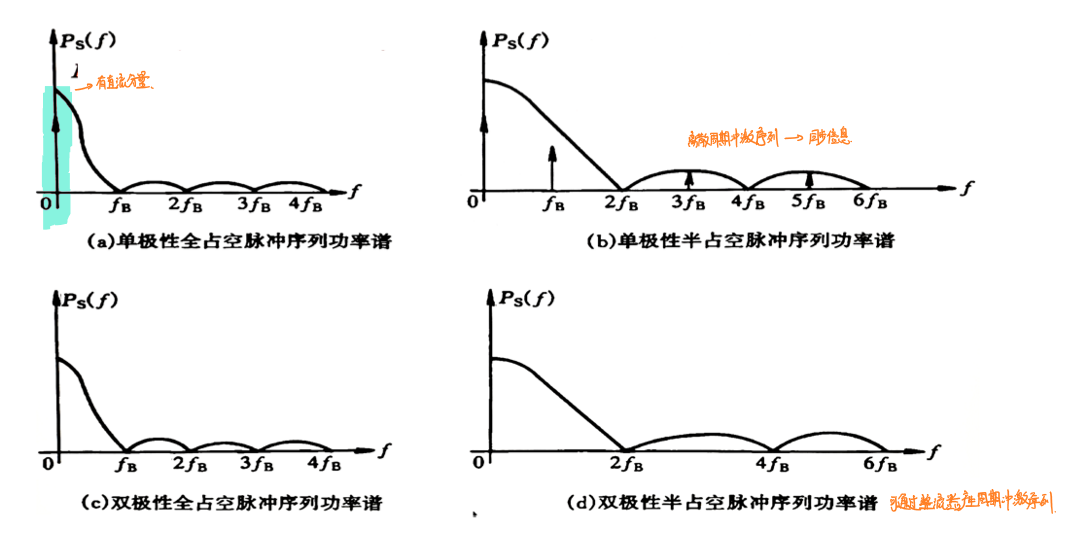
无直流分量在频域内的直接体现为0频时没有冲激信号，单极性不归零码(a)和单极性归零码(b)都存在直流分量，因此不适合用于传输。但是单极性归零码存在一个周期性的冲激序列，可以直接作为定时脉冲使用。
对双极性不归零码而言，不能直接提取定时脉冲，分离出定时脉冲的过程也比较复杂，因此不适用于传输。
对双极性归零码而言，虽然不能直接提取定时脉冲，但可以通过使用一个整流器转换为单极性归零码，从而提取出定时脉冲，且无直流分量，因此双极性归零码在数字基带传输中得到广泛应用。

除了上述四类码型外，还有差分码，时钟脉冲和输入单极性数字信号做异或运算/模二加法，得到输入信号的差分码。
差分码在接收端收到的极性与发送端完全相反时，也能够正确的判决。在此不详述。

AMI码和HDB₃编码

AMI码

AMI码是传号交替反转码的缩写，AMI码是一种双极不归零码，其编码规则如下：
* 消息编码中的0保持不变
* 消息编码中的1在AMI码中为1或-1，1和-1交替出现

例如：
消息编码： 1.0.0.1.1.1
其AMI码： +1.0.0.-1.1.-1

因此AMI码可以通过交替出现的极性观察传输过程中是否出现误码。
但是，当消息编码中含有过长的连0信号时（如：0000000），会给定时脉冲的提取造成困难，为了改进AMI码在长0信号下的传输问题，HDB₃码应运而生。

HDB₃ 码

HDB₃的编码规则基本和AMI码相同，但相比于AMI码，其规定在连续三个0信号出现时加入一个破坏脉冲V以防止过长0信号导致定时脉冲难以提取的问题。HDB₃码的编码规则如下：
1. 给定一个初始符号以指定消息编码中起始1的极性，使用AMI编码方式对消息进行编码。起始1的极性与初始符号的极性相反。
2. 当有连续4个0信号出现时，第四个0信号改为破坏脉冲V，对破坏脉冲的极性有如下规定：
i）V的极性交替反转（高优先级）
ii）破坏脉冲的极性与前一个“1”的极性相同（V视作1）
3. 在V的极性不满足条件2时，连0信号的第一个0变为补性码B'，B'的极性与其后一个V的极性相同。B'后的1全部反转极性。
4. V和B'保留极性，并替换为“1”。

例如：指定符号位为“+”：
消息编码：10000 0000 0000 0000 1
AMI编码： -10000 0000 0000 0000 1
加入破坏脉冲：-1000-V 000V 000-V 000V 1
加入补性码：-1000-V B’00V -B'00-V B'00V -1
HDB₃编码： -1000-1 1001 -100-1 1001 -1

HDB₃在解码时只需要找到连0信号两端极性相同的部分，替换为0即可：
HDB₃解码：-10000 0000 0000 0000 -1

曼彻斯特码

曼彻斯特码/双向码

曼彻斯特码是一种双极性不归零码，其01编码为脉冲信号的上升沿和下降沿，巧妙地解决了长连0信号由于电平不发生变化而导致的定时脉冲提取困难的问题。其编码规则为：
脉冲波形在同步脉冲间隔周期50%时：
- 脉冲上升沿表示逻辑1
- 脉冲下降沿表示逻辑0

例如：

但是曼彻斯特码在极性发生反转时容易发生译码错误，为了解决这个问题，引入了差分码的概念。

差分曼彻斯特码

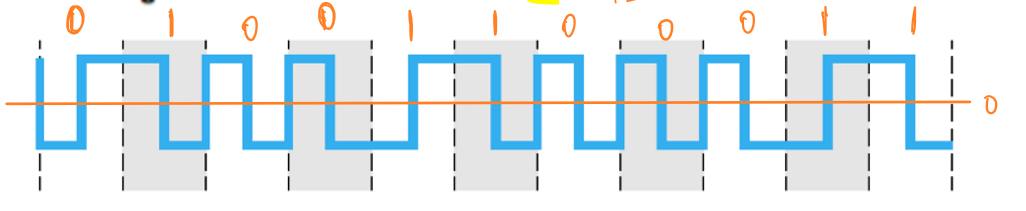
差分曼彻斯特码的编码规则为：
脉冲间隔开始时：
- 脉冲电平不发生变化（无触发沿）表示逻辑1 - 脉冲电平发生变化（有触发沿）表示逻辑0

例如：

基带波形的选择

除了考虑合适的码型外，还需要考虑使用什么形状的波形来表示选择的码型。
对波形的选择标准要求频谱图上的主瓣（即信号的有用带宽）后杂波的带宽越小越好，换言之，频谱函数收敛速度越快越好。
在方波脉冲、三角脉冲、升余弦脉冲中，升余弦脉冲的收敛速度最快，意味着杂波的带宽通常比较小，因此在数字基带通信中常选择升余弦脉冲作为基带波形。

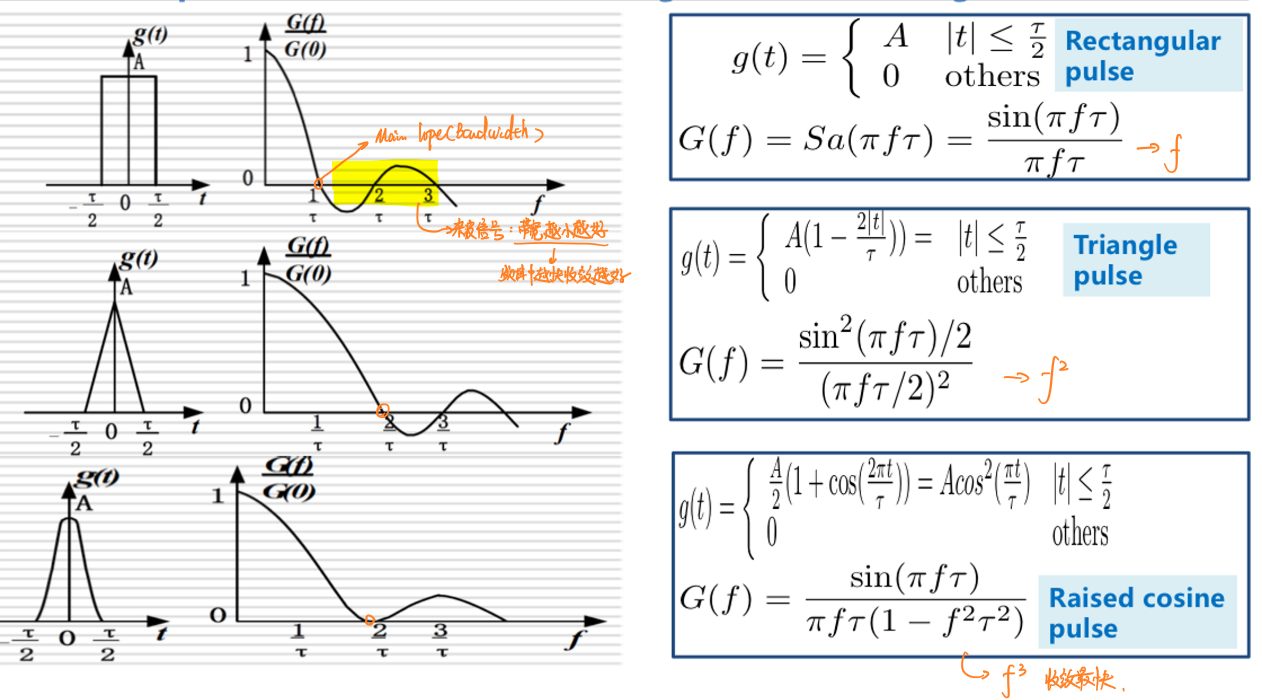
频谱分析

设脉冲信号\(g_1(t-nT_s)\)表示逻辑0，\(g_2(t-nT_s)\)表示逻辑1，假设随机脉冲序列在码元时间间隔\(T_s\)内逻辑1和0的出现是相互独立的，那么对任何一个数字信号\(s(t)\)都可以表示为：
\[s(t)=∑s_n(t)\] 其中: \[s_n(t)=\begin{cases} g_1(t-nT_s),\text{概率为}P\\ g_2(t-nT_s),\text{概率为}1-P\\ \end{cases}\]

\(s(t)\)的图示如下：

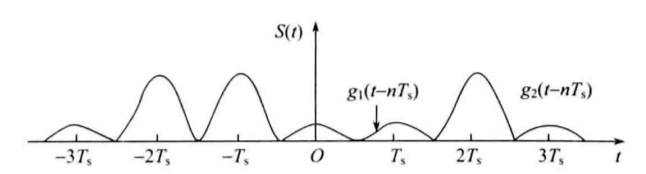
由于任何波形都可以分解为两个波形的叠加，考虑要知道基带信号中是否存在可以提供频谱分量的周期同步信息，因此将\(s(t)\)分解为能够提取同步信息的周期波形\(v(t)\)和随机信号\(u(t)\)：
\[s(t)=v(t)+u(t)\] 经过数学运算可知，\(v(t)\)的功率谱表示为：
\[P_v(f)=∑|f_s[PG_1(mf_s)+(1-P)G_2(mf_s)]|^2δ(f-mf_s)\] \(u(t)\)的功率谱表示为：
\[P_u(f)=f_sP(1-P)|G_1(f)-G_2(f)|^2\] 那么数字信号\(s(t)\)的频谱可以表示为：
\[\begin{aligned} P_s(f)&=P_u(f)+P_v(f)\\ &=∑|f_s[PG_1(mf_s)+(1-P)G_2(mf_s)]|^2δ(f-mf_s)+f_sP(1-P)|G_1(f)-G_2(f)|^2 \end{aligned}\] 化简为单边谱：
\[P_s(f)=2f_sP(1-P)|G_1(f)-G_2(f)|^2+f^2_s|PG_1(0)+(1-P)G_2(0)|^2δ(f)+2f_s^2∑|[PG_1(mf_s)+(1-P)G_2(mf_s)]|^2δ(f-mf_s)\] 可以发现这个单边谱公式由三部分组成：
\(f^2_s|PG_1(0)+(1-P)G_2(0)|^2δ(f)\)：在零频时的冲激信号，即信号的直流分量。
\(2f_s^2∑|[PG_1(mf_s)+(1-P)G_2(mf_s)]|^2δ(f-mf_s)\)：周期冲激序列，即可以提取用于同步的定时脉冲。
\(2f_sP(1-P)|G_1(f)-G_2(f)|^2\):连续谱分量，由随机信号产生，极大地影响频谱效率。
下图表示了符号持续时间\(τ\)和对应频谱带宽的关系：

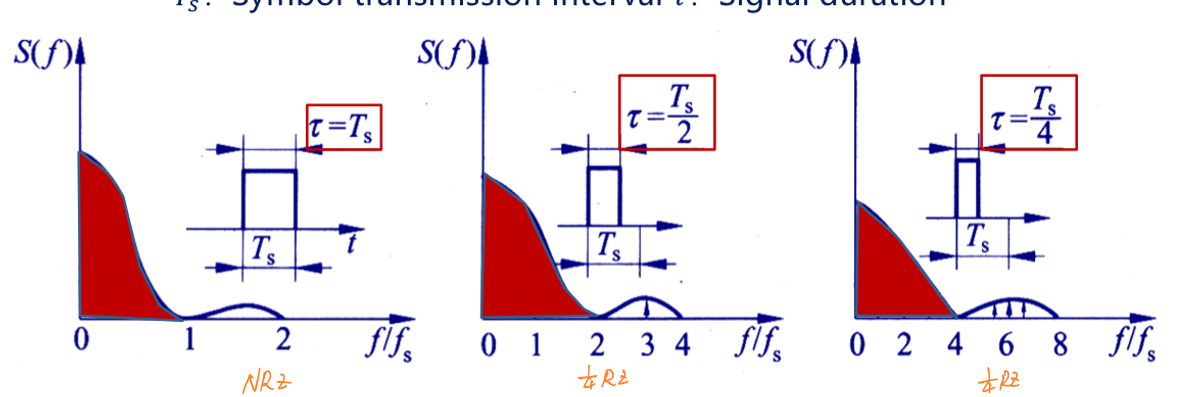
可以发现，符号持续时间越长，占用带宽越小。