10. 无码间串扰的数字基带传输系统

无码间串扰的数字基带传输系统

码间串扰的产生

由于系统的带宽有限，单个字符信号的脉冲发生了失真，使得波形发生延展、含有拖尾，波形延展到其他码元时间间隔中时，会对其他字符的抽样产生干扰，称为码间串扰。

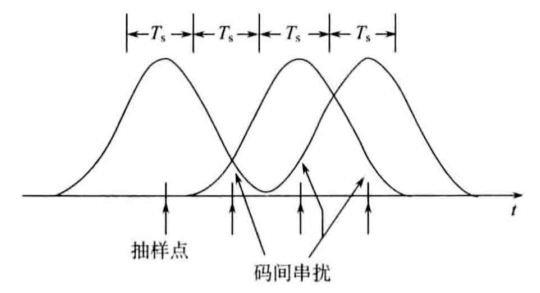
码间串扰与系统的带宽有关，系统的带宽越小，字符脉冲的拖尾就会越长越严重，发生码间串扰的可能性越大。

码间串扰的数学分析

数字信号\(d(t)=∑a(b)δ(t-nT)\)通过信道和接受滤波器后表示为：
\[y(t)=d(t)*h(t)+n_R(t)=∑a_nh(t-nT_s)+n_R(t)\] 其中\(n_R(t)\)表示窄带噪声。
经过采样周期为\(T_s\)的采样后：
\[y(kT_s+t_0)=∑a_nh(kT_s+t_0-nT_s)+n_R(kT_s+t_0)+a_kh(t_0)\] 其中：
\(a_kh(t_0)\)是第\(k\)个字符采样后波形的主瓣。
\(a_nh(kT_s+t_0-nT_s)\)是采样后波形的拖尾。
\(n_R(kT_s+t_0)\)是采样后的窄带噪声。
可以发现，要想消除码间串扰，就要让采样后的波形中不含有\(a_nh(kT_s+t_0-nT_s)\)一项，即系统的时域方程满足下列等式：
\[h(kT_s)=\begin{cases} Const, k=0 \\ 0, k≠0 \text{ 除了采样时刻，其余时间波形的采样值为0} \end{cases}\] 有两种方式可以使得系统波形满足\(a_nh(kT_s+t_0-nT_s)=0\)：
1. 系统波形正好在\(t_0+T_s\)时戛然而止
2. 系统波形虽然有拖尾，但是拖尾在每一个\(t_0+kT_S,k≠0\)的时刻为0。

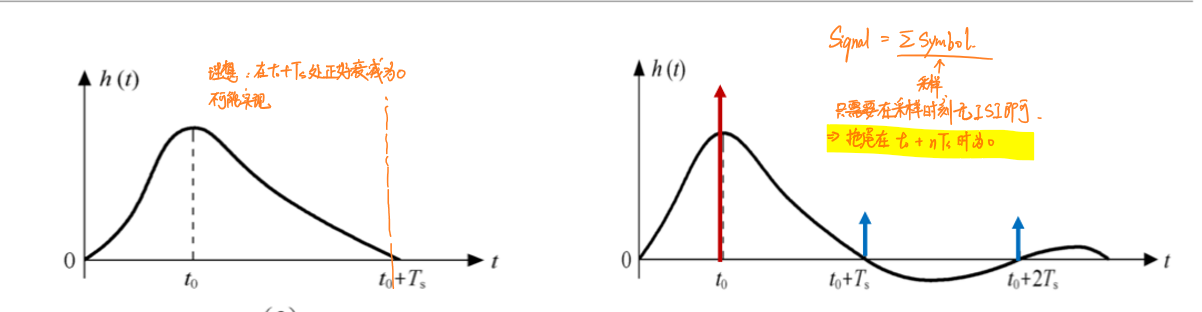
方案1无法在现实的电路中完成，因此现实中基本采用方法2来设计无码间串扰的系统。 下面推导符合上述条件的系统方程\(H(ω)\)：
根据傅里叶反变换：\(h(kT_s)=\frac{1}{2π}∫H(ω)e^{jωkT_s}dω\)
由于一个采样周期只有一个字符被抽样，因此修改积分上限，提取出一个抽样周期内的频谱函数(称为剪切)：
\[h(kT_s)=\frac{1}{2π}∑_i∫_{(2i-1)π/T_s}^{(2i+1)π/T_s}H(ω)e^{jωkT_s}dω\] 令\(ω'=ω-\frac{2iπ}{T}\)（称为时移）,
\[\begin{aligned} h(kT_s)&=\frac{1}{2π}∑_i∫_{-π/T_s}^{π/T_s}H(ω'+\frac{2iπ}{T})e^{jω'kT_s}e^{2πikj}dω'\\ &=\frac{1}{2π}∑_i∫_{-π/T_s}^{π/T_s}H(ω'+\frac{2iπ}{T})e^{jω'kT_s}dω'\\ &=\frac{1}{2π}∫_{-π/T_s}^{π/T_s}∑_iH(ω'+\frac{2iπ}{T})e^{jω'kT_s}dω' \end{aligned}\] 剪切、时移、叠加的物理意义如下图所示：

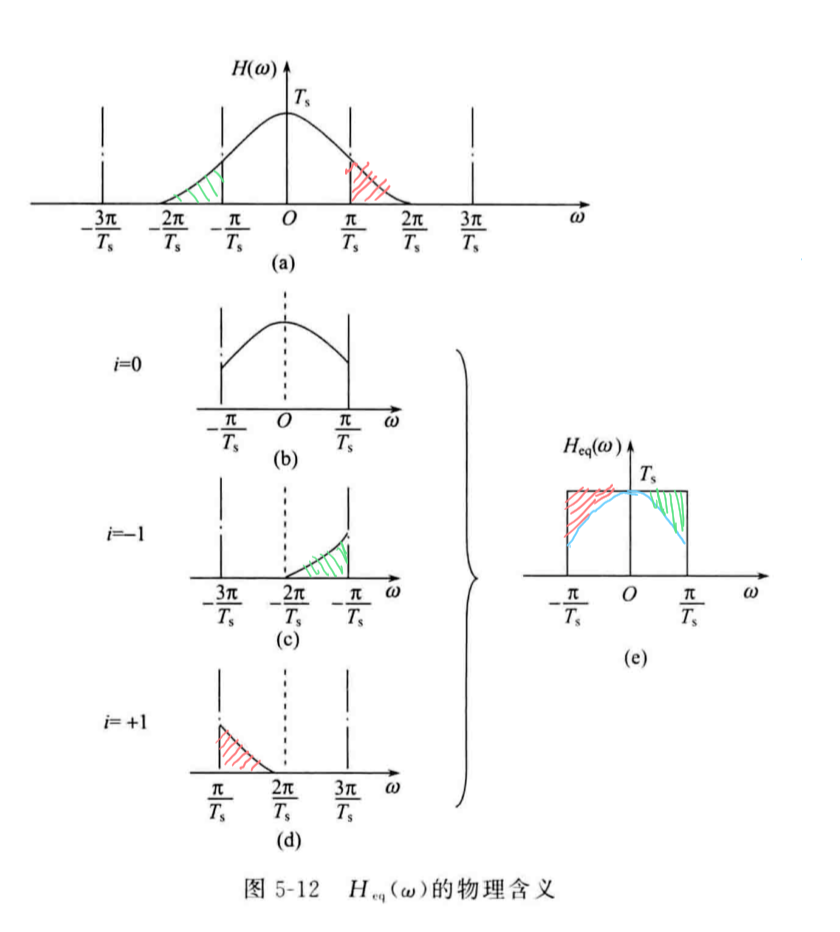
那么就得到了\(H(ω)\)的等效替代式子：
\[H_{eq}(ω)=∑_iH(ω'+\frac{2iπ}{T}),|ω|≤\frac{π}{T_s}\] \(H_{eq}(ω)\)的物理意义是将切断的各部分平移到\(|ω|≤\frac{π}{T_s}\)内对应叠加求和，简称切断叠加。
那么将该式子带入\(h(kT_s)\)需要满足的条件中，得到频域中，系统方程等价为：
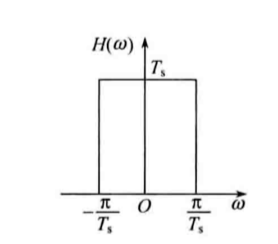
\[H(ω)=\begin{cases} ∑H(ω+\frac{2πi}{T_s})=T_s, |ω|≤\frac{π}{T_s} \\ 0, |ω|>\frac{π}{T_s} \text{ 除了采样时刻，其余时间波形的采样值为0} \end{cases}\] 即，当且仅当系统的等效频谱在为一个在\(±\frac{π}{T_s}\)上的门函数时，这个系统可以满足没有码间串扰，该定律称为奈奎斯特第一定律。

导出结论

• 满足奈奎斯特第一定律时，频谱图的带宽称为奈奎斯特带宽\(B_N\),\(B_N=\frac{1}{2T_s}Hz\)。
  
• 奈奎斯特间隔为：\(T_s=\frac{1}{2B_N}\)。
  
• 当采样周期为奈奎斯特间隔的整数倍（\(T_s=\frac{Const}{2B_N}\)）时，可以使得每次采样时信号拖尾的采样值都为0，系统无码间串扰。对应的数据传输速率为：\(R_B=\frac{1}{nT_s}\)。
  
• 系统支持的最大的传输速率为\(R_{B|max}=\frac{1}{T_s}=2B_N\)，当且仅当： \[\frac{R_{B|max}}{R_B}=Const\] 时，系统无码间串扰。
  
• 由频谱利用率\(η=\frac{R_B}{B}\)，系统最大的频谱利用率为\(η=\frac{2B_N}{B_n}=2\)。

无码间串扰系统

在频域中，要想使得系统频谱图为一个门函数，有两种方法：
1. 理想低通滤波器 2. 滚降滤波器 3. 部分响应系统

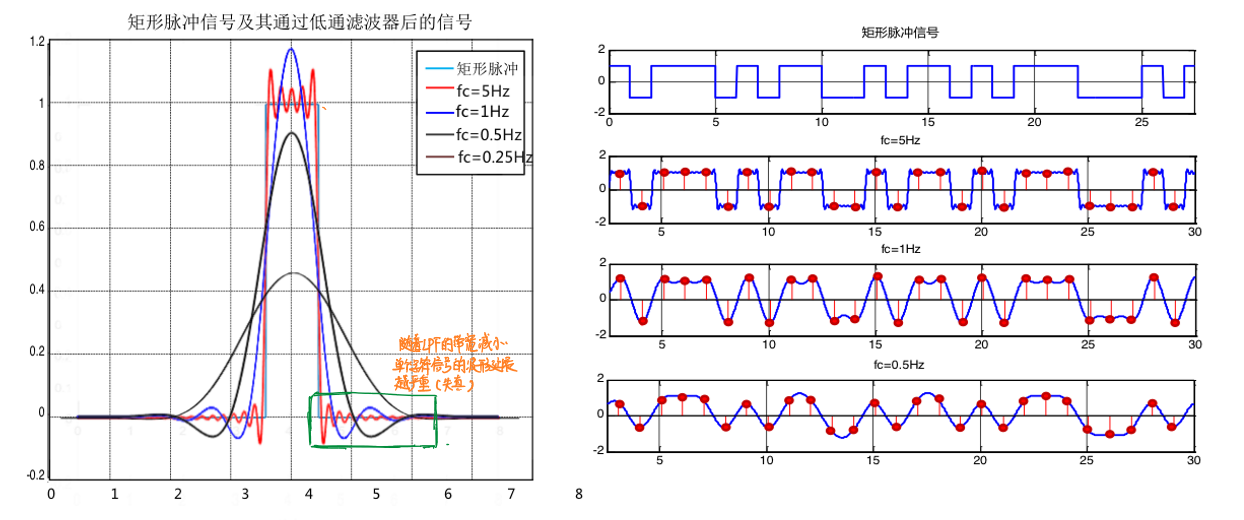
理想低通滤波器

理想低通滤波器的频谱正好是一个门函数：

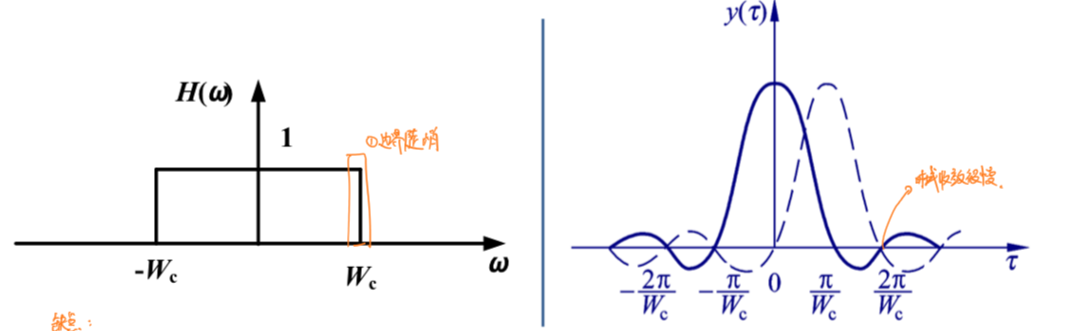
但是，可以从理想低通滤波器系统的频谱和波形图看出：理想低通滤波器有边界陡峭、难以实现、且时域中Sa函数收敛较慢的特点，因此考虑采用其他方法模拟等效理想低通滤波器的频谱。

滚降滤波器

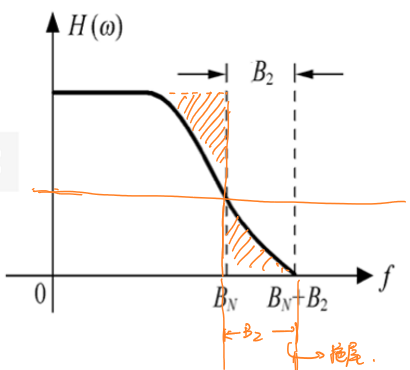
滚降滤波器的基本思路是在理想低通滤波器频谱后加入一段奇对称的频谱，使得被剪切、时移、叠加后的等效频谱中奇对称的一半正好可以填充另一半，得到一个门函数的频谱，这种方法称为滚降。

常常被选用的奇函数为反比例函数和升余弦函数（即余弦函数+常数）：

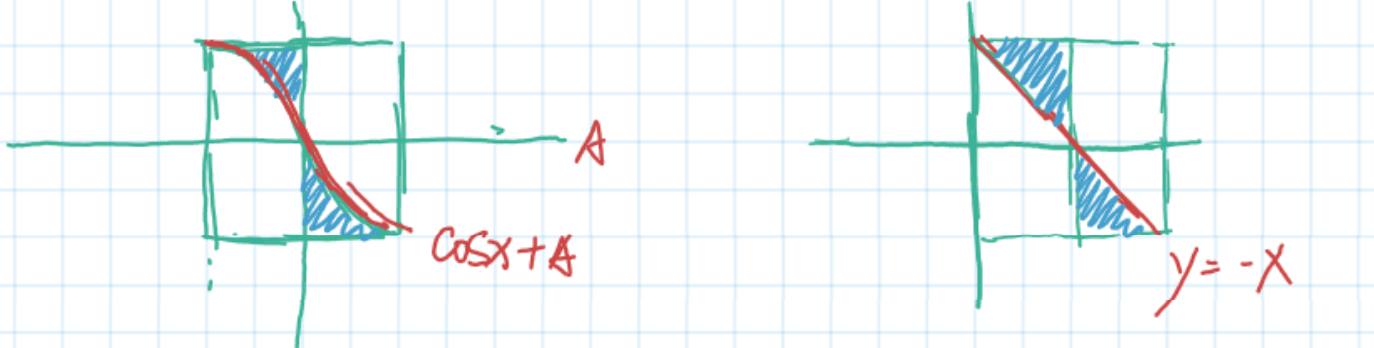
设奇对称信号的带宽为\(B_2\),那么滚降后的系统带宽为\(B_N+B_2\)。
滚降滤波器的系统方程可以表示为： \[H(ω)=\begin{cases} Const, 0≤ω≤B_N\\ f(ω), B_N≤ω≤B_N+B_2\\ 0,ω≥B_N+B_2 \end{cases}\] > 根据系统方程可以将滚降系统的频谱分为：非滚降区、滚降区和截止区。

定义滚降系数\(α=\frac{B_2}{B_N}\)，那么系统带宽又可以写作：
\[B=(1+α)B_N,0≤α≤1\] 频谱利用效率为:\(η=\frac{2}{1+α}\)
系统所支持的无码间串扰的最大速率为:\(R_{B|max}=2B_N\) 可以发现，\(α\)越大，系统带宽就越大，系统有效性下降，但是从频谱图上来看，\(α\)越大，系统波形拖尾越小，可靠性上升。

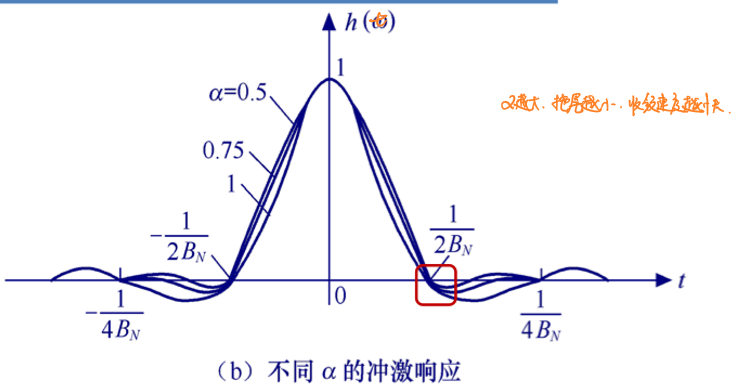
全滚降滤波器

\(α=1\)时的滤波器称为全滚降滤波器，全滚降滤波器没有非滚降段，系统方程表示为：
\[H(ω)=\begin{cases} f(ω), 0≤ω≤2B_N\\ 0,ω≥2B_N \end{cases}\] 此时系统的带宽为\(B=2B_N\)。

部分响应系统*

滚降滤波器虽然可以解决理想低通滤波器在实际系统设计中无法应用的问题，但是其频谱效率只有\(\frac{2}{1+α}\)，不能达到理想低通滤波器\(η=2\)的效果。部分响应系统通过人为地引入码间串扰来改善这一问题。 部分响应系统的基本设想是使用两个波形相同，但是各自时移\(\frac{T_s}{2}\)的脉冲信号传输一个码元：

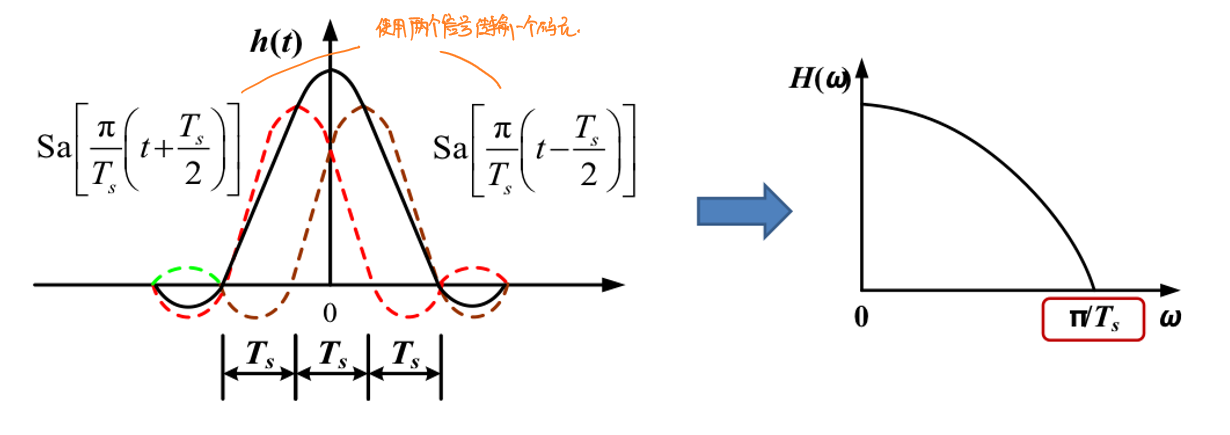
虽然部分响应系统在每一个采样时刻都存在码间串扰，但是这个码间串扰仅由表达一个码元的相邻两个脉冲引起，这个特性使得在接收端可以消除码间串扰。

系统类型	\(R_{Bmax}\)	\(B\)	\(η\)
理想低通滤波器	\(2B_N\)	\(B_N\)	\(2\)
滚降滤波器	\(2B_N\)	\((1+α)B_N\)	\(\frac{2}{1+α}\)
全滚降滤波器	\(2B_N\)	\(2B_N\)	\(1\)
部分响应系统	\(2B_N\)	\(B_N\)	\(2\)

时域均衡*

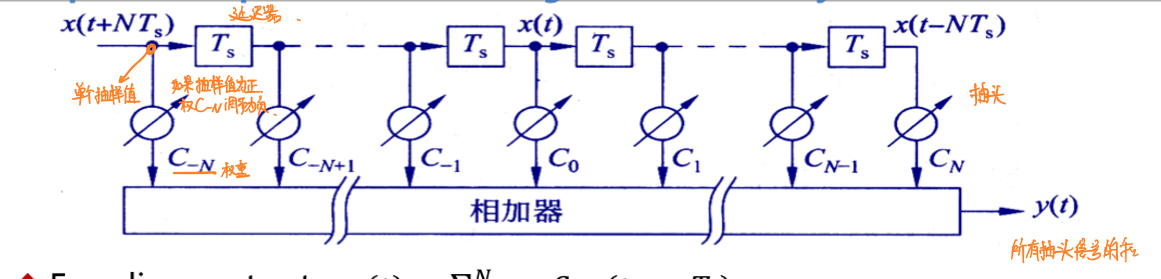
由于信道是时变系统，信道总会使得信号产生码间串扰。解决这一问题的方法是在接收机与接收滤波器之间增加一个均衡器\(E_x\)，通过均衡使得波形满足奈奎斯特第一定律进而消除码间串扰。均衡的方式有两种：时域均衡和频域均衡。本课只介绍时域均衡。
时域均衡的基本思想是在\(t+n,n≠0\)的时刻对采样信号叠加一个完全相反的冲激信号以抵消原本在采样时刻存在的非零电平，迫使\(x(t+nT_s)=0\)。

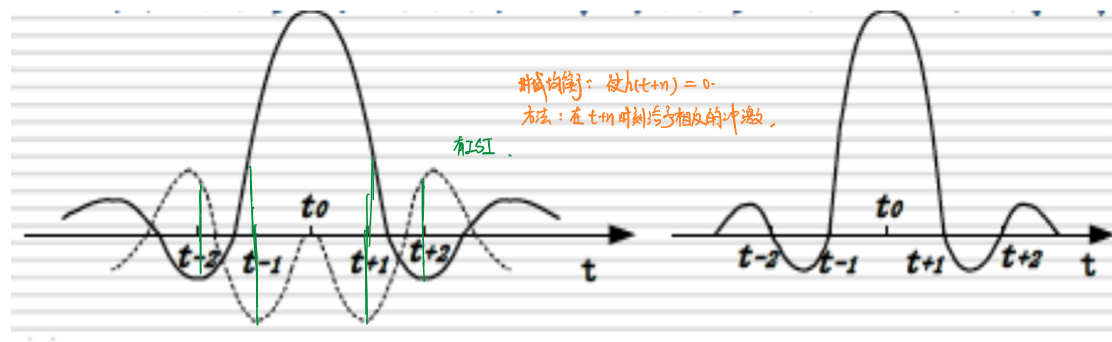
时域均衡器由若干个延迟器和自动调整权重的抽头以及相加器组成。延迟器的作用是确保获取\(x(t)\)在每一个\(nT_s\)上的抽样值，由自动调整权重的抽头赋予冲激信号一个与抽样值完全相反的权重、并与抽样值抵消，得到抽头信号。理论上，抽头信号只会在\(x(t)\)时有值。最后相加器将所有抽头信号相加，得到满足奈奎斯特第一定律的输出信号。