11. 数字基带系统的抗噪性分析
本文最后更新于 2025年6月4日 晚上
数字基带系统的抗噪性分析
抽样判决器
在接收端,设通过接收端滤波器的信号为\(x(t)\),它由传输信息\(s(t)\)和窄带高斯白噪声\(n_R(t)\)两部分构成。接下来,信号\(x(t)\)将通过抽样判决器,抽样判决器以\(f_s\)的抽样频率对其进行抽样,并对每一个抽样结果进行判断,决定抽样结果为数字逻辑“1”还是逻辑“0”。抽样判决器的工作原理可以表示为:
\[m'(kT_s)=\begin{cases}
1, x(kT_s)>V_d\\
0,x(kT_s)<V_d
\end{cases}\] \(V_d\)称为判决阈值。
误码率
数字基带系统在抽样判决器处的判决错误是产生误码率的重要原因,误码率\(P_e\)可以表示为两个条件概率之和:
\[P_e=P(0)P(\frac{1}{0})+P(1)P(\frac{0}{1})\] \(P(0)P(\frac{1}{0})\):原本的电平为0,误判为1的概率。
\(P(1)P(\frac{0}{1})\):原本的电平为1,误判为0的概率。
抽样判决器判决错误的主要原因是\(x(t)\)中包含的窄带高斯白噪声\(n_R(t)\)对判决结果产生了影响。
设\(n_R(t)\)的方差为\(σ_n^2\)、均值为0,则其概率密度函数为:
\[f(n)=\frac{1}{√(2π)σ_n}e^{-\frac{n^2}{2σ_n^2}}\] 并假设\(s(t)\)在为逻辑“0”的时刻电平为0,在为逻辑“1”的时刻电平对应其幅值\(A\),那么\(x(kT_s)\)可以表示为:
\[x(kT_s)=\begin{cases}
A+n_R(kT_s),logic-1\\
n_R(kT_s),logic-0
\end{cases}\] 那么,在发送逻辑“0”的时刻,\(x(kT_s)\)只包含\(n_R(t)\),发送“0”的概率密度函数为:
\[f_0(x)=\frac{1}{√(2π)σ_n}e^{-\frac{n^2}{2σ_n^2}}\] 当\(x(kT_s)\)的值大于\(V_d\)时,抽样判决器将原本为0的电平\(x(kT_s)\)误判为1,该概率可以表示为:
\[P_{e0}=∫_{V_d}^∞f_0(x)dx=∫_{V_d}^∞\frac{1}{√(2π)σ_n}e^{-\frac{n^2}{2σ_n^2}}dx\] 同理可以得到,当\(x(kT_s)\)的值小于\(V_d\)时原本抽样判决器原本为1的电平\(x(kT_s)\)误判为0,该概率可以表示为:
\[P_{e1}=∫_∞^{V_d}f_0(x)dx=∫_∞^{V_d}\frac{1}{√(2π)σ_n}e^{-\frac{n^2}{2σ_n^2}}dx\] 那么总的误码率就可以表示为:
\[P_e=P(0)P_{e0}+P(1)P_{e1}\] 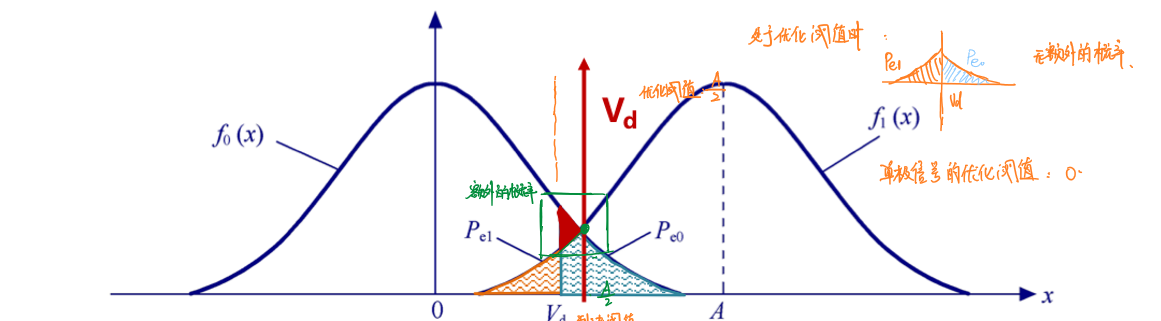
图示中的涂色部分表示误码率的两个条件概率,可以发现,只有当\(V_d=\frac{A}{2}\)时,“额外的概率”(图中红色部分所示)才能被抵消为0,此时误码率最小,\(V_d=\frac{A}{2}\)称为优化阈值。
在优化阈值下重新计算误码率,可以得到:
\[P_e=\frac{1}{2}erfc(\frac{A}{2√2σ_n})\] \(A\)与信号的功率有关,\(σ_n\)与噪声的功率有关。可以发现,在优化阈值下,影响误码率的唯一因素为信噪比。
对于单极性信号,其平均功率为\(S=\frac{A^2}{2}\),因此单极性信号的信噪比为:
\[SNR_u=\frac{A^2}{2σ^2}\] 此时误码率为:
\[P_e=\frac{1}{2}erfc(\frac{√SNR_u}{2})\] 对于双极性信号,其平均功率为\(S={A^2}\),因此双极性信号的信噪比为:
\[SNR_b=\frac{A^2}{σ^2}\] 此时误码率为:
\[P_e=\frac{1}{2}erfc(√{\frac{SNR_b}{2}})\] 比较两者的误码率,可以发现双极性信号的误码率总是优于单极性信号的误码率。
眼图
眼图是一种能够表现数字基带系统噪声和码间串扰的图像,它由示波器的余晖效应使得若干个\(T_s\)内的波形在示波器屏幕上叠加得到。
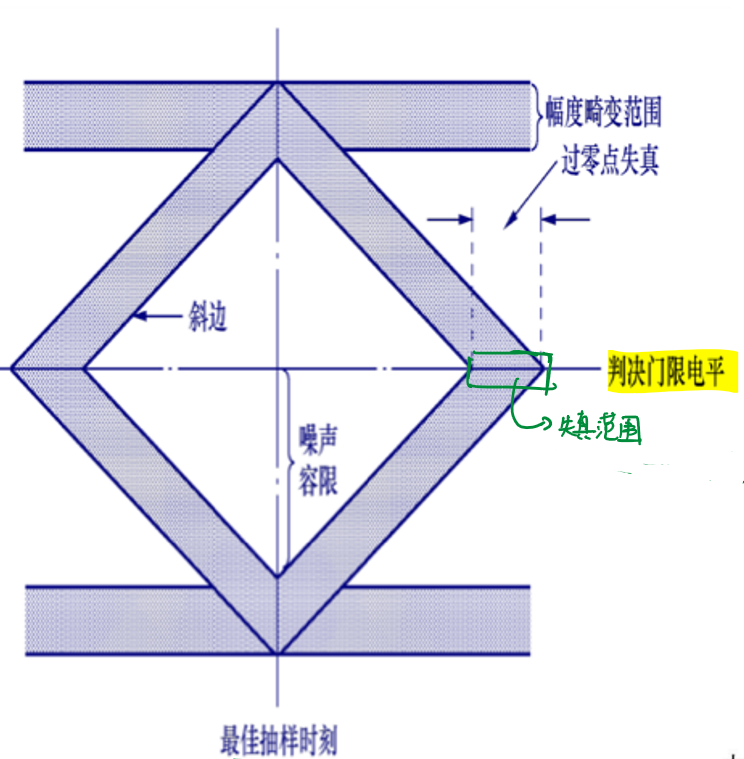
直观通过眼图判断系统抗噪性的指标为:
- 眼图是否清晰
- 系统的信噪比越高,眼图越清晰。
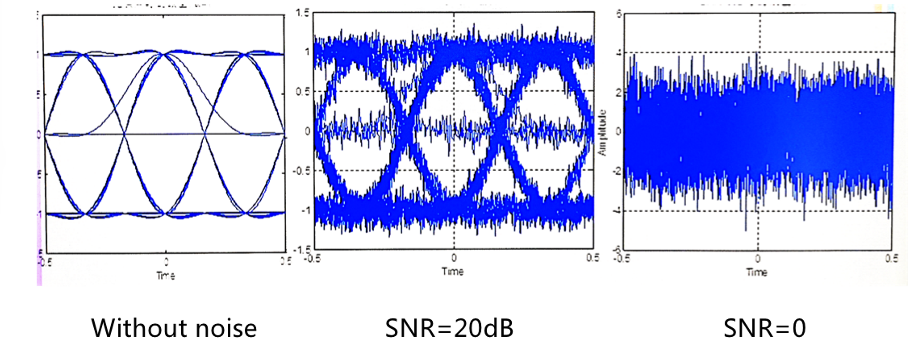
- 系统的信噪比越高,眼图越清晰。
- “眼睛”的开闭程度
- 系统的滚降系数越大,“眼睛”张开程度越大。
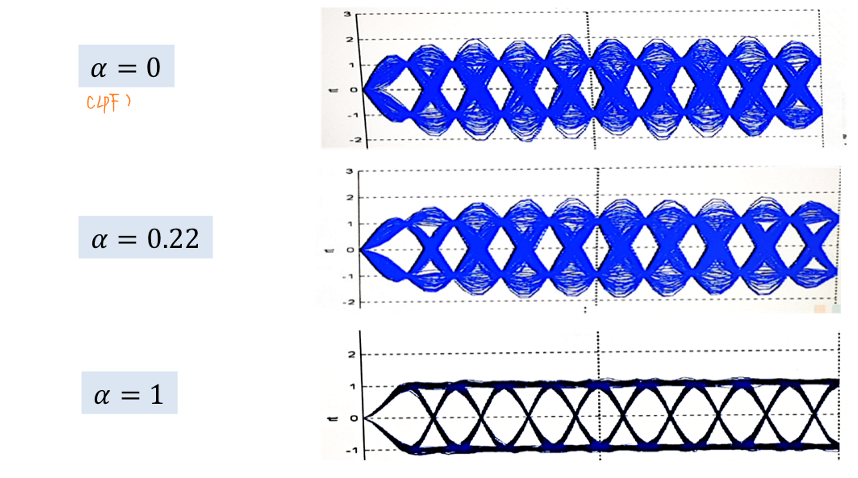
- 系统的滚降系数越大,“眼睛”张开程度越大。